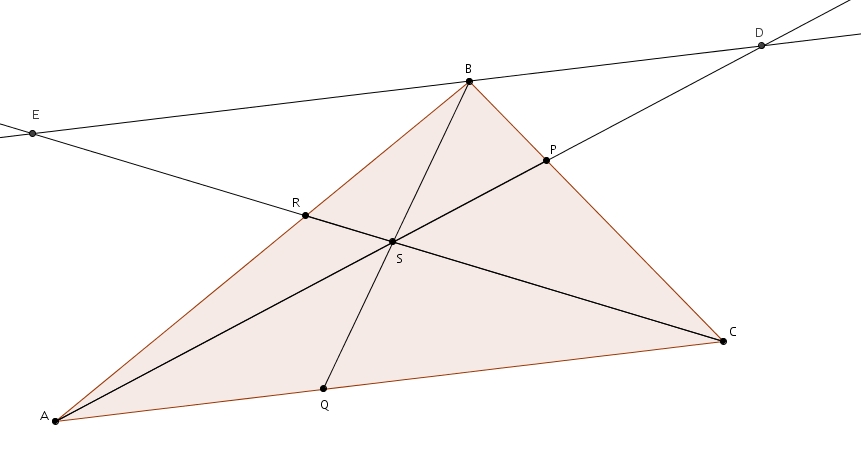
Le théorème de Ceva concerne les segments reliant sommets et côtés opposés dans les triangles. Considérons le triangle 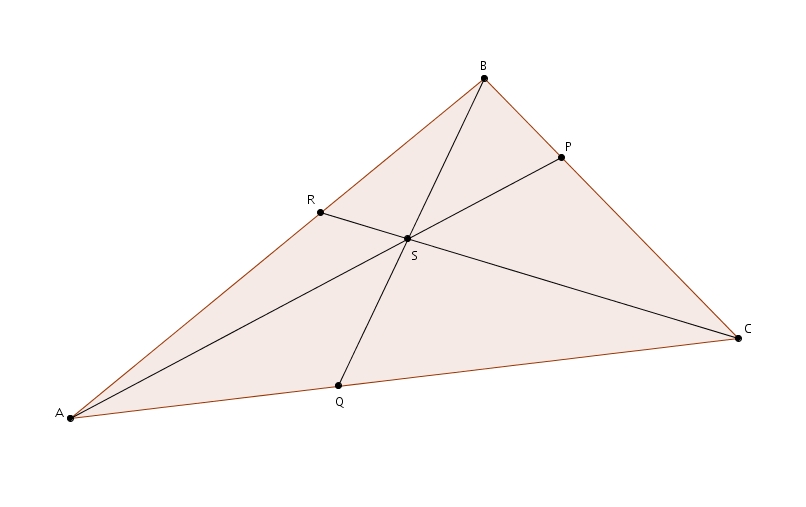 ABC suivant.
ABC suivant.
Plaçons P sur BC, Q sur AC et R sur AB. Les segments AP, BQ et CR se rencontrent en S si et seulement si

Il existe plusieurs démonstrations différentes de ce résultat. Traçons l’unique parallèle à AC passant par B. Prolongeons les segments AP et CR de telle sorte qu’ils coupent la parallèle respectivement en D et E. Nous avons à notre disposition une armée de triangles semblables. Il suffit de choisir les bonnes combinaisons.
- 1. Les angles BDP et CAP sont des angles alternes-internes isométriques formés par des parallèles. Les angles APC et DPB sont isométriques puisqu’ils sont opposés par le sommet. Les triangles APC et DPB sont donc semblables par le cas de similitude A-A. Grâce à cette similitude, on tire la proportion suivante
 2. Les angles RCA et REB sont des angles alternes-internes isométriques formés par des parallèles. Les angles CRA et ERB sont isométriques puisqu’ils sont opposés par le sommet. Les triangles CRA et ERB sont donc semblables par le cas de similitude A-A. Grâce à cette similitude, on tire la proportion suivante
2. Les angles RCA et REB sont des angles alternes-internes isométriques formés par des parallèles. Les angles CRA et ERB sont isométriques puisqu’ils sont opposés par le sommet. Les triangles CRA et ERB sont donc semblables par le cas de similitude A-A. Grâce à cette similitude, on tire la proportion suivante
- 3. Les angles SCQ et SEB sont des angles alternes-internes isométriques formés par des parallèles (déjà montré). Les angles QSC et BSE sont isométriques puisqu’ils sont opposés par le sommet. Les triangles QSC et BSE sont donc semblables par le cas de similitude A-A. Grâce à cette similitude, on tire la proportion suivante
 4. Enfin, les angles SAQ et SDB sont des angles alternes-internes isométriques formés par des parallèles (déjà montré). Les angles ASQ et DSB sont isométriques puisqu’ils sont opposés par le sommet. Les triangles ASQ et DSB sont donc semblables par le cas de similitude A-A. Grâce à cette similitude, on tire la proportion suivante
4. Enfin, les angles SAQ et SDB sont des angles alternes-internes isométriques formés par des parallèles (déjà montré). Les angles ASQ et DSB sont isométriques puisqu’ils sont opposés par le sommet. Les triangles ASQ et DSB sont donc semblables par le cas de similitude A-A. Grâce à cette similitude, on tire la proportion suivante
![]() Grâce à 3 et 4, on tire
Grâce à 3 et 4, on tire
![]() qu’on peut aussi écrire comme
qu’on peut aussi écrire comme
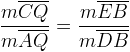 En multipliant
En multipliant
 et en utilisant le dernier résultat ainsi que les résultats 1 et 2, on obtient
et en utilisant le dernier résultat ainsi que les résultats 1 et 2, on obtient
![]() ce qui nous permet d’écrire finalement
ce qui nous permet d’écrire finalement

Il reste à fournir la preuve de la réciproque. Supposons que les segments AP et BQ se rencontrent en S et plaçons R sur AB de telle sorte que
 Traçons CS et prolongeons CS jusqu’à AB. CS coupe AB en R’.
Traçons CS et prolongeons CS jusqu’à AB. CS coupe AB en R’.
Or, si les segments AP, BQ et CR’ sont concourants, alors, par le Théorème de Ceva (celui-là même que l’on vient de prouver), on trouve
 Cependant, en rappelant notre hypothèse,
Cependant, en rappelant notre hypothèse,
 cela implique que
cela implique que
![]() Et en additionnant 1 de chaque côté…
Et en additionnant 1 de chaque côté…
![]() on obtient
on obtient
![]() et donc
et donc
![]() On peut réécrire les numérateurs
On peut réécrire les numérateurs
![]() afin de conclure
afin de conclure
![]() c’est-à dire que R’ et R sont confondus. La réciproque est prouvée.
c’est-à dire que R’ et R sont confondus. La réciproque est prouvée.
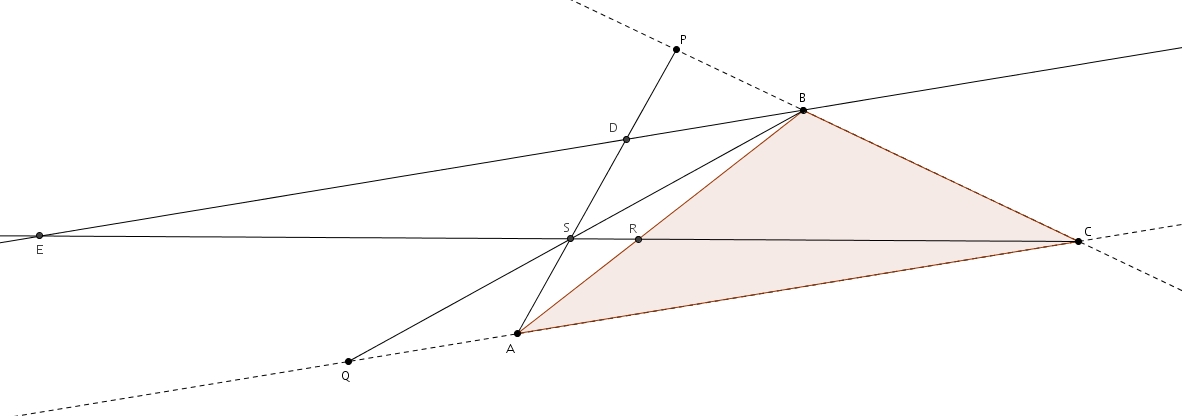
Les points PQR ne sont pas nécessairement sur les côtés du triangles : ils peuvent se trouver sur les prolongements des côtés, tel qu’illustré dans le figure suivante :
 On trace la parallèle à AC passant par B de la même façon afin d’obtenir
On trace la parallèle à AC passant par B de la même façon afin d’obtenir
Tout le raisonnement ci-haut reste valide.
Le théorème de Ceva peut se trouver très utile lorsque vient le temps de fournir la preuve que des segments dans un triangle se rencontrent en un point. Dans ce billet et ce celui-ci on prouve que les médianes, les hauteurs et les bissectrices d’un triangle sont concourantes. Nous allons revisiter ces preuves avec le théorème de Ceva. Il s’avère que le travail sera beaucoup moins fastidieux.
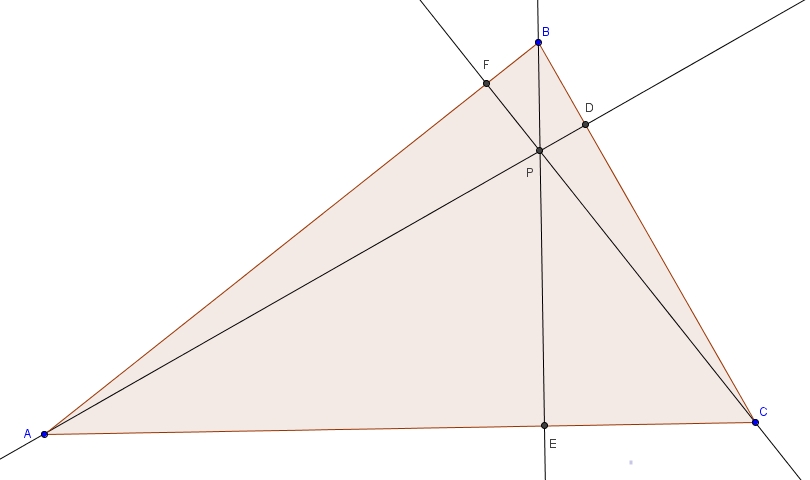
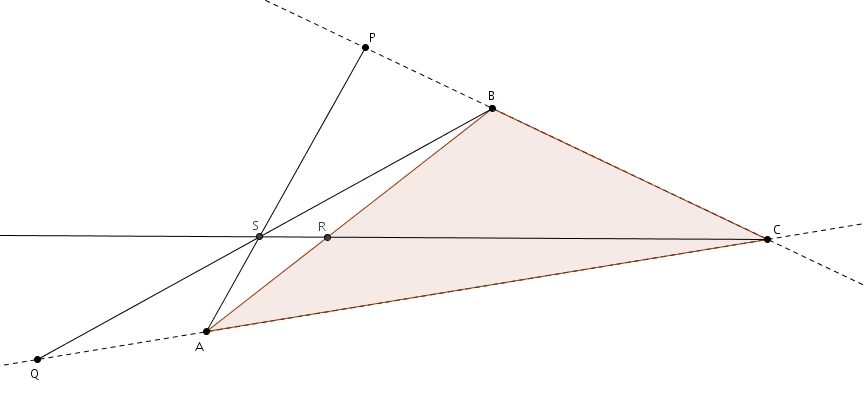
Les médianes
Dans un triangle ABC, on trace les médianes AD, BE et CF. 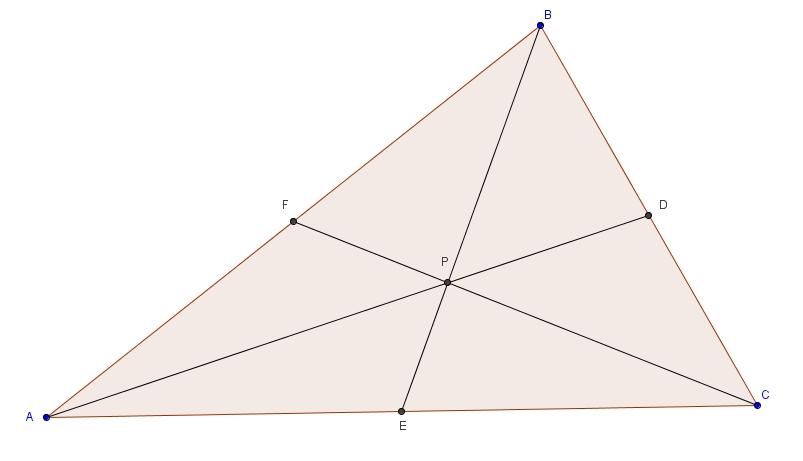 Par définition même de médiane, on sait que
Par définition même de médiane, on sait que
![]() Il va sans dire que l’on trouve
Il va sans dire que l’on trouve
![]()
et par le Théorème de Ceva, on peut affirmer que les médianes sont concourantes en P.
Les hauteurs
Dans le triangle ABC, on trace les hauteurs AD, BE et CF.
Les triangles BFC et ADB sont tous deux rectangles et partagent l’angle FBD. On peut donc affirmer qu’ils sont semblables par le cas de similitude AA. On tire cette proportion
![]()
Les triangles AEB et AFC sont tous deux rectangles et partagent l’angle FAE. On peut donc affirmer qu’ils sont semblables par le cas de similitude AA. On tire cette proportion
![]()
Les triangles CDA et CEB sont tous deux rectangles et partagent l’angle DCE. On peut donc affirmer qu’ils sont semblables par le cas de similitude AA. On tire cette proportion
![]()
Il suffit de multiplier ces trois égalités afin d’obtenir
![]()
Par le théorème de Ceva, on est en mesure d’affirmer que les hauteurs sont concourantes en P.
Les bissectrices
Dans le triangle ABC, on trace les bissectrices AD, BE, CF.
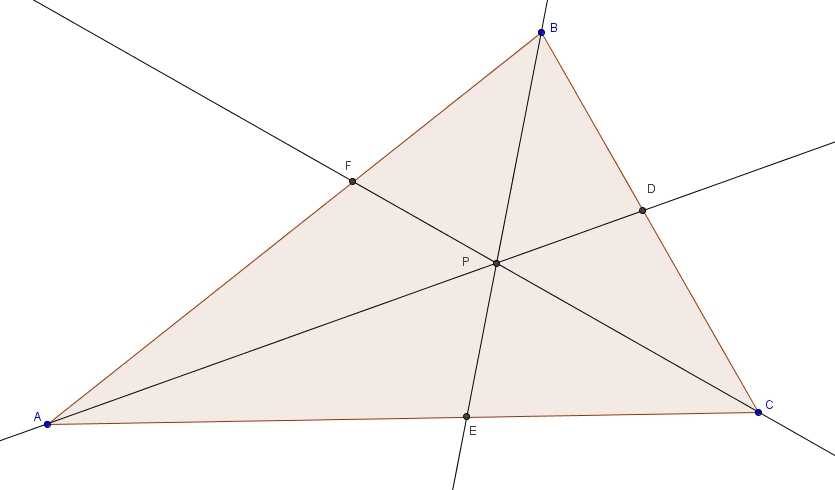 Dans un triangle, les bissectrices divisent toujours le côté opposé en deux segments proportionnels aux côtés de l’angle. Il suffit donc de tirer, avec, respectivement, les bissectrices CF, AD et BE,
Dans un triangle, les bissectrices divisent toujours le côté opposé en deux segments proportionnels aux côtés de l’angle. Il suffit donc de tirer, avec, respectivement, les bissectrices CF, AD et BE,
![]() et donc en multipliant
et donc en multipliant
![]()
Par le théorème de Ceva, on peut donc affirmer que les trois bissectrices sont concourantes en P.
Référence : Alfred S. Posamentier et Charles T. Salkind (1996), Challenging Problems In Geometry