Surprise !

En quatrième secondaire on travaille avec les élèves les conditions minimales de similitude des triangles.  Une attention particulière est portée aux relations métriques dans les triangles rectangles dans lesquels on a tracé la hauteur issue de l’angle droit (ou la hauteur relative à l’hypoténuse).  Voici un petit résultat qui fait changement des exercices du manuel.  Les élèves apprécient.

Considérez le triangle rectangle $ABC$ ci-dessous (rectangle en $C$)

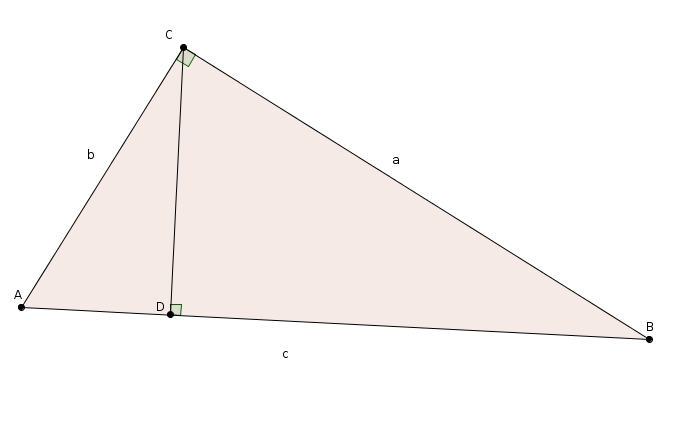
On trace la hauteur issue de l’angle droit.  Elle coupe $\overline{AB}$ de façon perpendiculaire en $D$.  Le “petit” triangle $ACD$ et le “grand” triangle $ABC$ sont tous les deux rectangles et partagent tous les deux l’angle $A$.  Il sont donc semblables par le cas de similitude AA. $$\mathrm{△}ABC\sim \mathrm{△}ACD$$Les côtés homologues des triangles semblables sont dans le même rapport.  Considérons les “petites” cathètes et les hypoténuses des deux triangles.  On obtient la proportion suivante$$\frac{m\overline{AC}}{m\overline{AD}}=\frac{m\overline{AB}}{m\overline{AC}}$$de laquelle on tire $${\left(m\overline{AC}\right)}^2=m\overline{AB}\cdot m\overline{AD}$$Le “moyen” triangle $CBD$ et le “grand” triangle $ABC$ sont tous les deux rectangles et partagent tous les deux l’angle $B$.  Il sont donc semblables par le cas de similitude AA.$$\mathrm{△}ABC\sim \mathrm{△}CBD$$En considérant les “grandes” cathètes et les hypoténuses des deux triangles, on obtient la proportion suivante$$\frac{m\overline{BC}}{m\overline{BD}}=\frac{m\overline{AB}}{m\overline{BC}}$$de laquelle on tire $${\left(m\overline{BC}\right)}^2=m\overline{AB}\cdot m\overline{BD}$$En additionnant les deux résultats précédents on obtient $${\left(m\overline{AC}\right)}^2+{\left(m\overline{BC}\right)}^2=m\overline{AB}\cdot m\overline{AD}+m\overline{AB}\cdot m\overline{BD}$$et en effectuant la mise en évidence simple à droite$${\left(m\overline{AC}\right)}^2+{\left(m\overline{BC}\right)}^2=m\overline{AB}\cdot (m\overline{AD}+m\overline{BD})$$Les segments $AD$ et $BD$ forment justement le segment $AB$, l’hypoténuse du grand triangle rectangle.  On a donc en substituant $${\left(m\overline{AC}\right)}^2+{\left(m\overline{BC}\right)}^2=m\overline{AB}\cdot m\overline{AB}$$ou tout simplement $${\left(m\overline{AC}\right)}^2+{\left(m\overline{BC}\right)}^2={\left(m\overline{AB}\right)}^2$$… la relation de Pythagore ! $$a^2+b^2=c^2$$