… mais un pas de géant pour l’inégalité des moyennes arithmétique et géométrique
L’inégalité des moyennes arithmétique et géométrique est une inégalité élémentaire très connue (et utile). La moyenne arithmétique \(A\) de deux nombres positifs \(a\) et \(b\) est \[A=\frac{a+b}{2}\]alors que la moyenne géométrique \(G\) [1] de deux nombres positifs \(a\) et \(b\) est \[G=\sqrt{ab}\]L’inégalité stipule que \[A\geq G\]
Pour 2 nombres
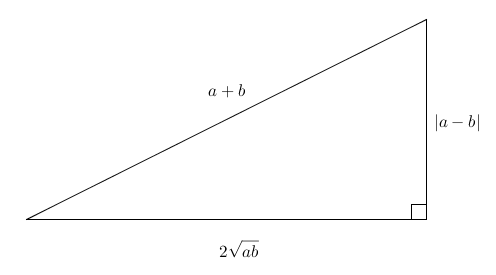
Le triangle est-il rectangle ? La cathète étant plus petite que l’hypoténuse, on a \(a+b>2\sqrt{ab}\) ou \(\frac{a+b}{2}> \sqrt{ab}\)
L’inégalité pour deux nombres positifs \(a\) et \(b\) est \[\frac{a+b}{2} \geq \sqrt{ab}\]On peut faire la démonstration de cette inégalité assez facilement. On observe d’abord que \(\left (\sqrt{\vphantom{b}a}-\sqrt{b} \right )^{2}\) étant un carré, c’est-à-dire un nombre positif, on a \[\left(\sqrt{\vphantom{b}a}-\sqrt{b}\right)^2 \geq 0\]Il est aussi évident qu’on a l’égalité si et seulement si \(\sqrt{\vphantom{b}a} = \sqrt{b}\). Ainsi, si \(\sqrt{\vphantom{b}a}\neq \sqrt{b}\), on a \[\left(\sqrt{\vphantom{b}a}-\sqrt{b}\right)^2 > 0\]On peut développer à gauche, \[a- 2\sqrt{ab} + b > 0\]ou, de manière équivalente, \[a + b > 2\sqrt{ab}\]ou encore \[\frac{a+b}{2} > \sqrt{ab}\]Voilà.
Qu’en est-il pour trois nombres ? Pour quatre nombres ? Pour \(n\) nombres ? L’inégalité tient-elle ? La réponse est oui. Pour trois nombres, on a \[\frac{a+b+c}{3} \geq \sqrt[3]{abc}\]avec égalité si et seulement si \(a=b=c\) et pour quatre, \[\frac{a + b + c + d}{4} \geq \sqrt[4]{abcd}\]avec égalité si et seulement si \(a=b=c=d\). Pour \(n\) nombres, c’est \[\frac{a_{1}+a_{2}+a_{3}+\dots+a_{n}}{n}\geq \sqrt[n]{a_{1}a_{2}a_{3}\cdots a_{n}}\]toujours avec égalité si \[a_{1}=a_{2}=a_{3}=\dots=a_{n}\]
Pour \(n\) nombres
L’inégalité des moyennes arithmétique et géométrique était en fait une belle excuse dans ce billet pour vous présenter le petit bijou d’induction mathématique qui suit. Il me semble que dans chaque livre ou manuel, lorsque vient le temps de faire l’introduction à l’induction mathématique, on prend grand soin d’expliquer l’induction « qui monte » et celle « qui descend » … avec plusieurs exemples d’induction « qui monte » mais, c’est peut-être une impression personnelle, sans jamais fournir un exemple authentique d’induction qui descend. En voici un remarquable.
La démonstration suivante est attribuée à Augustin Louis Cauchy (1789-1857) dans son Cours d’Analyse, publié en 1821.
Sur la recommandation de Niven [2], on s’attaque d’abord aux cas \(n=3\) et \(n=4\), à titre d’exemples, puisque la démonstration de Cauchy peut être assez redoutable pour un néophyte. On commence donc par démontrer, avec les quatre nombres positifs \(a\), \(b\), \(c\) et \(d\), que \[\frac{a+b+c+d}{4}\geq \sqrt[4]{abcd}\]Il est clair qu’on a l’égalité si et seulement si \[a = b= c= d\]et on suppose donc qu’au moins deux de ces nombres ne sont pas égaux, par exemple \(a \neq b\) et on s’attaque à l’inégalité stricte \[\frac{a+b+c+d}{4}> \sqrt[4]{abcd}\]On sait que \[\frac{a+b}{2}>\sqrt{ab}\]et \[\frac{c+d}{2}\geq \sqrt{cd}\]puisqu’il s’agit de l’inégalité avec deux nombres (\(n=2\)), démontrée ci-haut. En effectuant la somme de ces inégalités, on obtient \[\frac{a+b+c+d}{2} >\sqrt{ab} + \sqrt{cd}\]En réutilisant l’inégalité de deux nombres une deuxième fois, avec les membres de droite, on obtient \[\frac{\sqrt{ab}+\sqrt{cd}}{2} \geq \sqrt{\sqrt{ab}\sqrt{cd}}\]ou \[\frac{\sqrt{ab}+\sqrt{cd}}{2} \geq \sqrt{\sqrt{abcd}}\]ce qui fait \[\frac{\sqrt{ab}+\sqrt{cd}}{2}\geq \sqrt[4]{abcd}\]ou en multipliant par \(2\) \[\sqrt{ab} + \sqrt{cd} \geq 2 \sqrt[4]{abcd}\]L’inégalité pour quatre nombres découle donc de ces deux inégalités \begin{align*}\frac{a+b+c+d}{2} &>\sqrt{ab} + \sqrt{cd} \geq 2 \sqrt[4]{abcd} \\ \\ \frac{a+b+c+d}{2} &> 2 \sqrt[4]{abcd} \\ \\ \frac{a+b+c+d}{4} &> \sqrt[4]{abcd} \end{align*} On note au passage qu’on obtient bien l’inégalité stricte comme résultat final. On cherche ensuite à démontrer, avec les trois nombres positifs \(a\), \(b\) et \(c\), que \[\frac{a+b+c}{3}\geq \sqrt[3]{abc}\]avec égalité si et seulement si \[a = b = c\]Comme pour le cas précédent, on suppose que \(a \neq b\) et on démontre l’inégalité stricte. On utilise le résultat précédent (le cas \(n = 4\)) \[\frac{a+b+c+d}{4} > \sqrt[4]{abcd}\]et on effectue la substitution suivante \[d = \sqrt[3]{abc}\]On obtient donc \[\frac{a+b+c+\sqrt[3]{abc}}{4} > \sqrt[4]{abc\sqrt[3]{abc}}\]Le membre de droite se simplifie à \begin{align*}\sqrt[4]{abc\sqrt[3]{abc}} &= \left(abc \left(abc\right)^{\frac{1}{3}}\right)^{\frac{1}{4}} \\ \\ &=\left(\left(a^{3}b^{3}c^{3}\right)^{\frac{1}{3}} \left(abc\right)^{\frac{1}{3}}\right)^{\frac{1}{4}} \\ \\ &= \left(\left(a^{4}b^{4}c^{4}\right)^{\frac{1}{3}}\right)^{\frac{1}{4}} \\ \\ &= \left(\left(\left(abc\right)^{4}\right)^{\frac{1}{3}}\right)^{\frac{1}{4}} \\ \\ &= \left(\left(abc\right)^{\frac{4}{3}}\right)^{\frac{1}{4}} \\ \\ &= \left(abc\right)^{\frac{1}{3}} \\ \\ &= \sqrt[3]{abc}\end{align*} ce qui fait \[\frac{a+b+c+\sqrt[3]{abc}}{4} > \sqrt[3]{abc}\]Et voilà ! Il suffit de multiplier par \(4\) \[a+ b + c + \sqrt[3]{abc} > 4 \sqrt[3]{abc}\]de soustraire \(\sqrt[3]{abc}\) de chaque côté \[a + b + c > 3\sqrt[3]{abc}\]et finalement de diviser par \(3\) \[\frac{a+b+c}{3}> \sqrt[3]{abc}\]
La preuve de Cauchy
On considère la proposition \(P_{n}\) suivante : pour \(n\) nombres positifs \(a_{1}\), \(a_{2}\), \(a_{3}\), … , \(a_{n}\), pas tous égaux, on a \[\frac{a_{1}+a_{2}+a_{3}+ \cdots + a_{n}}{n}>\sqrt[n]{a_{1}a_{2}a_{3}\cdots a_{n}}\]Afin d’alléger un peu la notation, on peut réécrire l’inégalité ci-dessous comme \[a_{1}+a_{2}+a_{3}+ \cdots +a_{n} > n\left(a_{1}a_{2}a_{3}\cdots a_{n}\right)^{\frac{1}{n}}\]On sait que \(P_{2}\) est vraie (c’est l’inégalité avec deux nombres, démontrée ci-haut). En s’inspirant de la démarche précédente (qui établissait au passage \(P_{3}\) et \(P_{4}\)), on établit \(P_{n}\) pour \(n\geq 3\). On y arrive en démontant ces deux résultats :
Premier résultat : Si la proposition \(P_{n}\) est vraie pour les nombres \(n\geq 3\), alors \(P_{n-1}\) est vraie aussi.
Deuxième résultat : Si la proposition \(P_{n}\) est vraie pour les nombres \(n \geq 3\), alors \(P_{2n}\) est vraie aussi.
Comme dans Niven [2], on peut voir que la combinaison de ces résultats démontre la proposition \(P_{n}\) pour tout \(n \geq 3\). On sait que \(P_{2}\) est vraie, donc le deuxième résultat nous dit que \[P_{4}, \; P_{8}, \; P_{16}, \;P_{32}, \; P_{64}, \; \cdots \]sont vraies aussi. Ainsi, pour montrer que la proposition \(P_{n}\) est vraie pour une valeur particulière de \(n\), il suffit d’aller chercher une puissance de \(2\) supérieure (ou égale) à \(n\), par le deuxième résultat, puis de « descendre » jusqu’à \(n\) par le premier résultat. Par exemple, pour établir \(P_{28}\), on irait jusqu’à \(P_{32}\) par le deuxième résultat, puis, par le premier, on obtiendrait successivement les propositions \[P_{31}, \; P_{30}, \; P_{29}, \;P_{28}\]Comment ne pas s’extasier devant autant de génie ?
On s’attaque d’abord à la démonstration que \(P_{n}\) implique \(P_{n-1}\). On suppose que (c’est notre hypothèse) \[a_{1}+a_{2}+a_{3}+ \cdots + a_{n} > n\left(a_{1}a_{2}a_{3}\cdots a_{n}\right)^{\frac{1}{n}}\]avec \(a_{1} \neq a_{2}\), et on remplace \(a_{n}\) par la moyenne géométrique \(g\) de \(a_{1}\), \(a_{2}\), … , \(a_{n-1}\), c’est-à-dire, par \(g = \left(a_{1}a_{2}a_{3}\cdots a_{n-1}\right)^{\frac{1}{n-1}}\). On obtient donc \[a_{1}+a_{2}+a_{3}+ \cdots + a_{n-1}+g > n\left(a_{1}a_{2}a_{3}\cdots a_{n-1}\, g\right)^{\frac{1}{n}}\]Puisque \begin{align*}g &= \left(a_{1}a_{2}a_{3}\cdots a_{n-1}\right)^{\frac{1}{n-1}} \\ \\ g^{n-1} &= a_{1}a_{2}a_{3}\cdots a_{n-1} \end{align*} l’inégalité précédente devient \begin{align*}a_{1}+a_{2}+a_{3}+ \cdots + a_{n-1}+g &> n\left(g^{n-1}g\right)^{\frac{1}{n}} \\ \\ a_{1}+a_{2}+a_{3}+ \cdots + a_{n-1}+g &> n\left(g^{n}\right)^{\frac{1}{n}} \\ \\ a_{1}+a_{2}+a_{3}+ \cdots + a_{n-1}+g &> ng\end{align*} En soustrayant \(g\) de chaque côté, on obtient \[a_{1}+a_{2}+a_{3}+ \cdots + a_{n-1} > \left(n-1\right)g\]ou \[a_{1}+a_{2}+a_{3}+ \cdots + a_{n-1} > \left(n-1\right)\left(a_{1}a_{2}a_{3}\cdots a_{n-1}\right)^{\frac{1}{n-1}}\]c’est-à-dire la proposition \(P_{n-1}\).
On s’attarde ensuite à démontrer que la proposition \(P_{n}\) implique \(P_{2n}\). Encore une fois, on suppose que \(a_{1} \neq a_{2}\). En utilisant le cas \(n = 2\), on sait que \begin{align*} a_{1} + a_{2} &> 2\sqrt{a_{1}a_{2}} \\ \\ a_{3} + a_{4} &\geq 2\sqrt{a_{3}a_{4}} \\ \\ a_{5} + a_{6} &> 2\sqrt{a_{5}a_{6}} \\ \\ &\cdots \\ \\ a_{2n-1} + a_{2n} &> 2\sqrt{a_{2n-1}a_{2n}} \end{align*} La somme de toutes ces inégalités correspond à l’inégalité stricte \[a_{1} + a_{2} + a_{3} + a_{4} + \cdots + a_{2n-1} + a_{2n} > 2\left(\sqrt{a_{1}a_{2}} + \sqrt{a_{3}a_{4}}+\sqrt{a_{5}a_{6}}+\cdots +\sqrt{a_{2n-1}a_{2n}}\right)\]On note qu’il y a bien \(n\) termes dans la grande parenthèse à droite. On applique donc la proposition \(P_{n}\) (notre hypothèse) aux \(n\) termes à droite. Ces termes pourraient être tous égaux, donc on obtient l’inégalité large \begin{align*}\sqrt{a_{1}a_{2}} + \sqrt{a_{3}a_{4}}+\cdots +\sqrt{a_{2n-1}a_{2n}} &\geq n\left(\sqrt{a_{1}a_{2}} \sqrt{a_{3}a_{4}}\cdots \sqrt{a_{2n-1}a_{2n}}\right)^{\frac{1}{n}}\\ \\ &\geq n\left(\sqrt{a_{1}a_{2}a_{3}\cdots a_{2n-1}a_{2n}}\right)^{\frac{1}{n}} \\ \\ &\geq n\left(\left(a_{1}a_{2}a_{3}\cdots a_{2n-1}a_{2n}\right)^{\frac{1}{2}}\right)^{\frac{1}{n}} \\ \\ &\geq n\left(a_{1}a_{2}a_{3}\cdots a_{2n-1}a_{2n}\right)^{\frac{1}{2n}}\end{align*} En multipliant l’inégalité précédente par \(2\), on obtient \[2\left(\sqrt{a_{1}a_{2}} + \sqrt{a_{3}a_{4}}+\cdots +\sqrt{a_{2n-1}a_{2n}}\right) \geq 2n\left(a_{1}a_{2}a_{3}\cdots a_{2n-1}a_{2n}\right)^{\frac{1}{2n}}\]ce qui nous permet d’établir \(P_{2n}\), en réutilisant \[a_{1} + a_{2} + a_{3} + a_{4} + \cdots + a_{2n-1} + a_{2n} > 2\left(\sqrt{a_{1}a_{2}} + \sqrt{a_{3}a_{4}}+\sqrt{a_{5}a_{6}}+\cdots +\sqrt{a_{2n-1}a_{2n}}\right) \geq 2n\left(a_{1}a_{2}a_{3}\cdots a_{2n-1}a_{2n}\right)^{\frac{1}{2n}}\] et donc \[a_{1} + a_{2} + a_{3} + a_{4} + \cdots + a_{2n-1} + a_{2n}>2n\left(a_{1}a_{2}a_{3}\cdots a_{2n}\right)^{\frac{1}{2n}}\]c’est-à-dire la proposition \(P_{2n}\).
\begin{align*} \; \\ \\ \; \end{align*}
[1] Les élèves se demandent quand est-ce qu’on utilise la moyenne géométrique. Par exemple, on l’utilise quand on veut calculer la moyenne de rapports ou de facteurs. On suppose qu’un employeur offre une augmentation salariale de \(30\%\) la première année (donc un salaire \(S\) est multiplié par \(1,\!30\)), \(10\%\) la deuxième et \(5\%\) la troisième. La moyenne arithmétique nous donnerait \[\frac{1,30S + 1,10S + 1,05S}{3} = 1,15S\]c’est-à-dire une augmentation salariale moyenne \(15\%\) par année. Or, ce n’est pas le cas (un petit calcul suffit à nous convaincre). L’augmentation moyenne \(G\) doit correspondre à \[1,30 \cdot 1,10 \cdot 1,05 S = G^{3}S\]ou \[G = \sqrt[3]{1,30\cdot 1,10 \cdot 1,05} = \sqrt[3]{1,5015} = 1,1451\]c’est-à-dire que l’augmentation moyenne n’est pas de \(15\%\) mais plutôt de \(14,\!51\%\). On note au passage que la moyenne géométrique \(G\) est plus petite (\(1,\!1451\)) que la moyenne arithmétique (\(1,\!15\)), tel qu’attendu.
[2] Niven, Ivan, Maxima and Minima Without Calculus, MAA, 1981
Autre référence :
Alsina, Claudi et Nelsen, Roger B., When Less is More, MAA, 2009