Pour une aire donnée, le rectangle possédant le plus petit périmètre est un carré.
On considère le carré suivant d’aire \(x^{2}\)
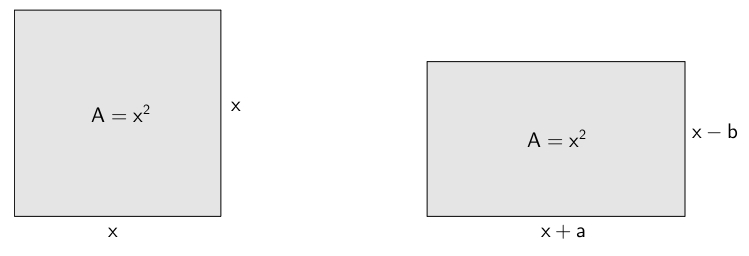
La mesure d’un de ses côtés est \(x\) et son périmètre est \(4x\). On considère ensuite un rectangle équivalent. Il est clair que si on augmente à la fois la longueur et la largueur, l’aire du rectangle sera indubitablement supérieure et, contrairement, si on diminue à la fois la longueur et la largeur, l’aire sera nécessairement plus petite. Il faut donc augmenter la longueur et diminuer la largeur (ou vice-versa). Les mesures des côtés du rectangle sont donc \(x-a\) et \(x-b\), où \(a\) et \(b\) sont deux nombres réels strictement positifs. Le périmètre du deuxième rectangle est\[4x+2\left(a-b\right)\]En quoi cela se compare-t-il avec le périmètre du carré ? Comme les rectangles sont équivalents, on a, en comparant les aires,\begin{align*}(x+a)(x-b)&=x^{2}\\ \\ x^2 +(a-b)x-ab&=x^{2}\\ \\ (a-b)x-ab&=0 \\ \\ a-b&=\frac{ab}{x}\end{align*}En substituant, le périmètre du deuxième rectangle devient\[4x+\frac{2ab}{x}\]et puisque\[a>0,\quad b>0,\quad x>0\]l’expression\[\frac{2ab}{x}>0\]est strictement positive. Cela nous permet de conclure que\[4x+\frac{2ab}{x}>4x\]On pose ensuite le problème suivant
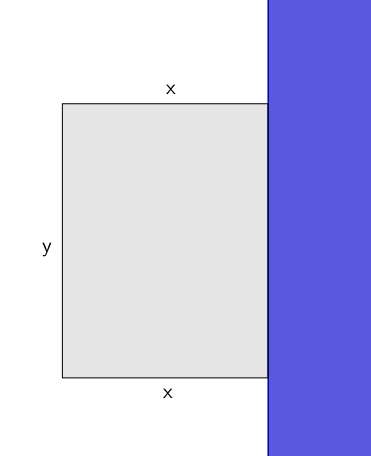
Un terrain rectangulaire d’aire A se trouve le long de la rive (rectiligne) d’une rivière. Quelle est la longueur minimale de la clôture nécessaire pour clôturer les trois autres côtés du terrain ?
La solution est-elle encore un carré ?
On a\[A=xy\] \[P=2x+y\]avec\[x>0, \quad y>0\]En substituant on obtient\[P = 2x + \frac{A}{x}\]On cherche à minimiser \(P\). En dérivant par rapport à \(x\) on obtient\[P’ = 2-\frac{A}{x^{2}}\]puis en résolvant \begin{align*}0&=2-\frac{A}{x^{2}} \\ \\ \frac{A}{x^{2}}&=2 \\ \\ A&=2x^{2} \\ \\ \frac{A}{2} &= x^{2} \\ \\ \pm \sqrt{\frac{A}{2}} &=x \\ \\ \pm\frac{\sqrt{2}}{2}\sqrt{A}&=x\end{align*}On ne retient que la racine positive puisque \(x>0\). Enfin comme \[P^{\prime \prime} = \frac{2A}{x^{3}}\]on a en remplaçant\[P^{\prime \prime}=\frac{2A}{\frac{\sqrt{2}}{2}\sqrt{A}}>0\]ce qui nous assure que notre solution\[x=\frac{\sqrt{2}}{2}\sqrt{A}\]est un minimum. Il est peut-être étonnant de prime abord de voir que\[x=\sqrt{A}\]n’est pas la solution et que le rectangle de plus petite aire n’est pas un carré ! C’est essentiellement contraire à l’intuition que l’on aurait pu se forger au départ. On peut obtenir une expression pour \(y\) \[y = \sqrt{2}\sqrt{A}\]et calculer ce qui donne, comme longueur de clôture,\begin{align*}2\frac{\sqrt{2}}{2}\sqrt{A} + \sqrt{2}\sqrt{A} &= 2\sqrt{2}\sqrt{A} \\ \\&\approx 2,\!8284\sqrt{A}\\ \\ &<3\sqrt{A}\end{align*}
Comme il est inutile de clôturer la rive, on n’a qu’à compter le plus grand côté une seule fois. Il semble donc normal, après réflexion, qu’on ait \(y>x\) dans la solution optimale.
Tiens, tiens, il n’y manque que le pop corn.
J’aime beaucoup.
Merci encore.
Tout le plaisir est mien ! Cette question m’a été posée cette semaine par une élève de quatrième secondaire (l’aire était spécifiée). J’imagine qu’on s’attendait à ce qu’elle utilise un outil technologique.