Vous avez dit une bonne question à choix multiples ?
 Inspiré de la question #25 du concours AMC-12A de l’année 2002. J’ai utilisé « parabole » plutôt que « représentation graphique d’une fonction polynomiale de degré \(n\) » pour ne pas effrayer nos élèves de quatrième secondaire.
Inspiré de la question #25 du concours AMC-12A de l’année 2002. J’ai utilisé « parabole » plutôt que « représentation graphique d’une fonction polynomiale de degré \(n\) » pour ne pas effrayer nos élèves de quatrième secondaire.
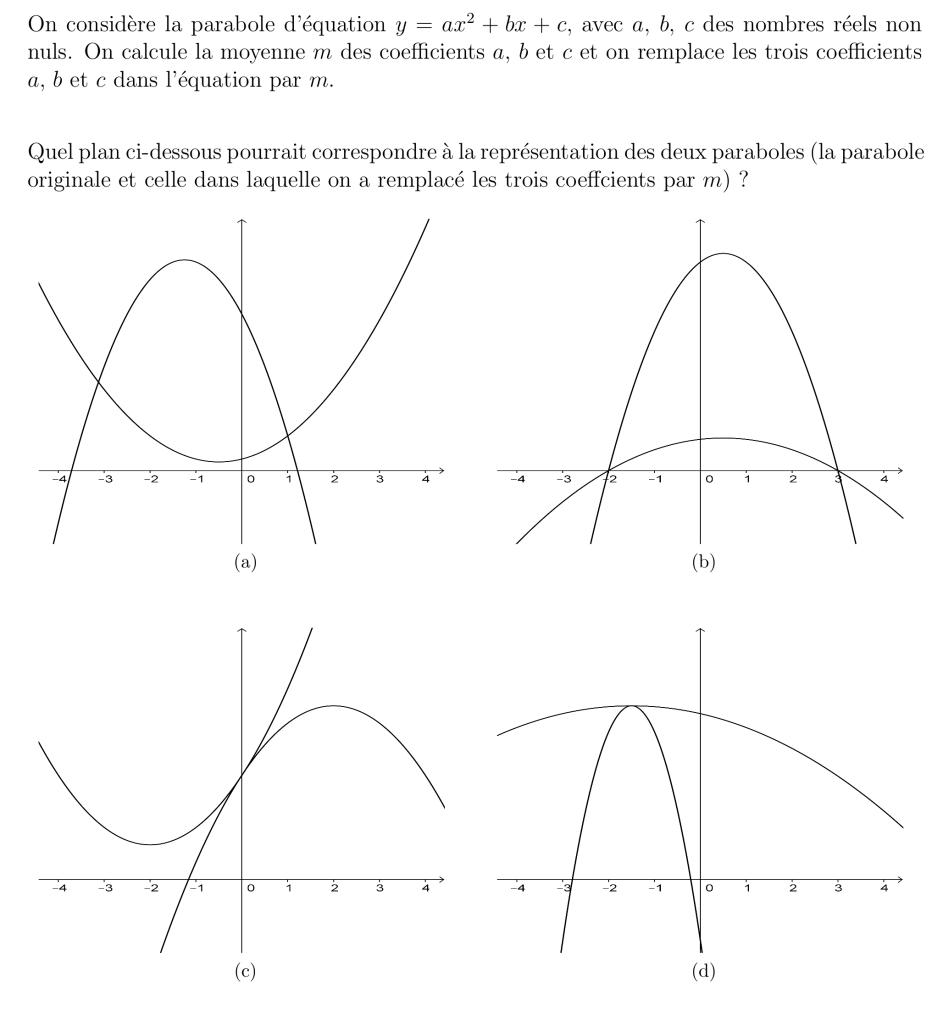
La parabole avec les coefficients m a un Delta égal à -3m^2, donc des racines complexes. Et un extremum en x=-1/2. La seule courbe vérifiant ces deux propriétés est sur le plan (a), donc je dirais (a).
Ou sinon… Avec x = 1, on a
y = a(1)^2 + b(1) + c = a + b + c
dans un cas et
y = m(1)^2 + m(1) + m = 3m
dans l’autre. Or, 3m = 3(a + b + c)/3 = a + b + c
Les deux paraboles se croisent donc en x = 1 et les coordonnées du point d’intersection sont (1, a + b + c).
Il n’y a qu’en a) que les deux paraboles se croisent en x = 1.