“A bicycle, certainly, but not THE bicycle,” said he. “I am familiar with forty-two different impressions left by tires. This, as you perceive, is a Dunlop, with a patch upon the outer cover. Heidegger’s tires were Palmer’s, leaving longitudinal stripes. Aveling, the mathematical master, was sure upon the point. Therefore, it is not Heidegger’s track.”
“The boy’s, then?”
“Possibly, if we could prove a bicycle to have been in his possession. But this we have utterly failed to do. This track, as you perceive, was made by a rider who was going from the direction of the school.”
“Or towards it?”
“No, no, my dear Watson. The more deeply sunk impression is, of course, the hind wheel, upon which the weight rests. You perceive several places where it has passed across and obliterated the more shallow mark of the front one. It was undoubtedly heading away from the school. It may or may not be connected with our inquiry, but we will follow it backwards before we go any farther.”
Arthur Conan Doyle (1903), The Adventure Of The Priory School
Voici les traces laissées par un vélo, des traces qu’on pourrait observer, par exemple, dans un sol boueux. J’ai attribué deux couleurs différentes aux traces, celle de la roue avant et celle de la roue arrière, afin qu’on puisse bien les distinguer sur l’image. Peut-on découvrir dans quel sens le vélo s’est déplacé ? De gauche à droite ou de droite à gauche ?
C’est un problème fort intéressant, résolu par John Conway, Peter Doyle, Jane Gilman, and Bill Thurston en 1991 dans un cours intitulé Geometry and the Imagination donné à Princeton et au Geometry Center de l’Université du Minnesota. La solution apparaît aussi dans le livre Which Way Did The Bicycle Go ? de Joseph D. E. Konhauser, Daniel J. Velleman et Stan Wagon (MAA, 1996). Le problème est inspiré du passage cité ci-dessus d’une nouvelle d’Arthur Conan Doyle dans laquelle son célèbre détective Sherlock Holmes se trouve pour une rare fois dans l’erreur.
Notre expérience à vélo peut nous mener à découvrir, de manière intuitive, la trace qui représente celle de la roue arrière et celle de la roue avant. On s’imagine faire des “s” en vélo à basse vitesse : la roue arrière parcourt une moins grande distance que la roue avant. Sur notre dessin, cela veut donc dire que la trace noire est celle de la roue arrière et la trace bleue celle de la roue avant. Mais cela ne nous indique pas dans quel sens le vélo s’est déplacé.
Le truc comporte deux aspects. D’abord, il faut observer que la distance entre les points de contact au sol de la roue avant et de la roue arrière est toujours constante (ou presque). Ensuite, on peut faire pivoter la roue avant avec le guidon (elle forme donc un angle avec le cadre) mais la roue arrière, elle, est fixe : elle garde toujours le même angle par rapport au cadre, et cet angle est nul. Ainsi, en examinant la trajectoire d’un vélo, la roue arrière est toujours tangente à la trace qu’elle laisse.
Ainsi, il est impossible que la trace bleue soit celle de la roue arrière car la courbe bleue possède des tangentes qui ne touchent pas la courbe noire.
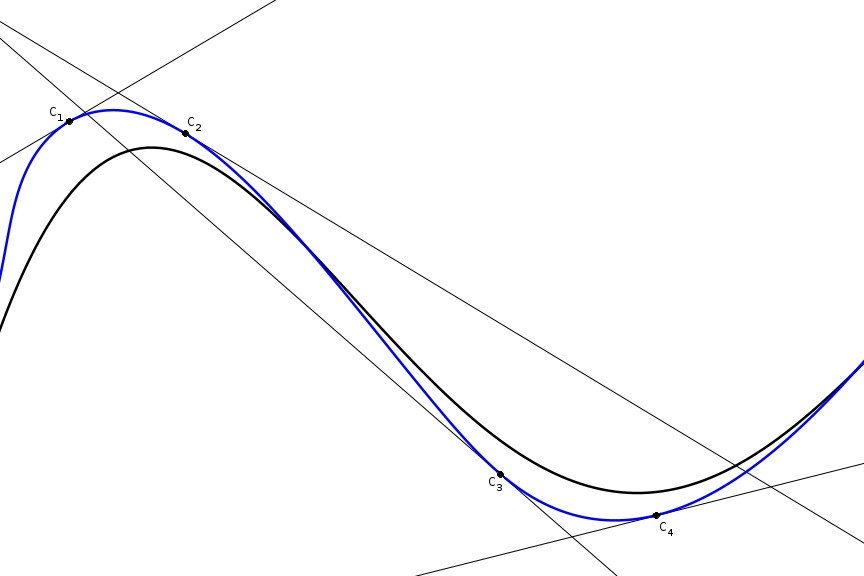La trace noire est donc celle de la roue arrière, tel qu’on l’avait deviné. De plus, si on examine des tangentes à différents points \(B_{i}\) sur la trace noire,
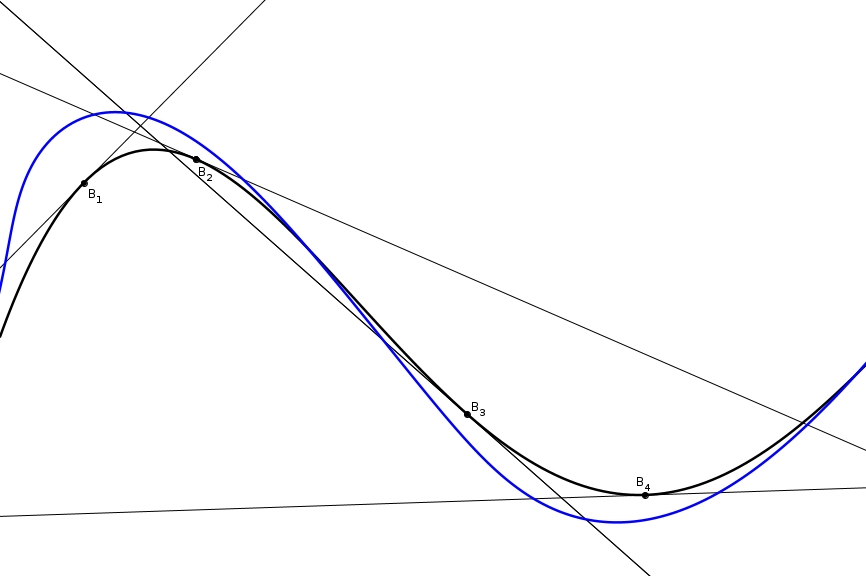on remarque que chacune de ces tangentes coupent la courbe bleue à deux endroits, \(A_{i}\) et \(C_{i}\).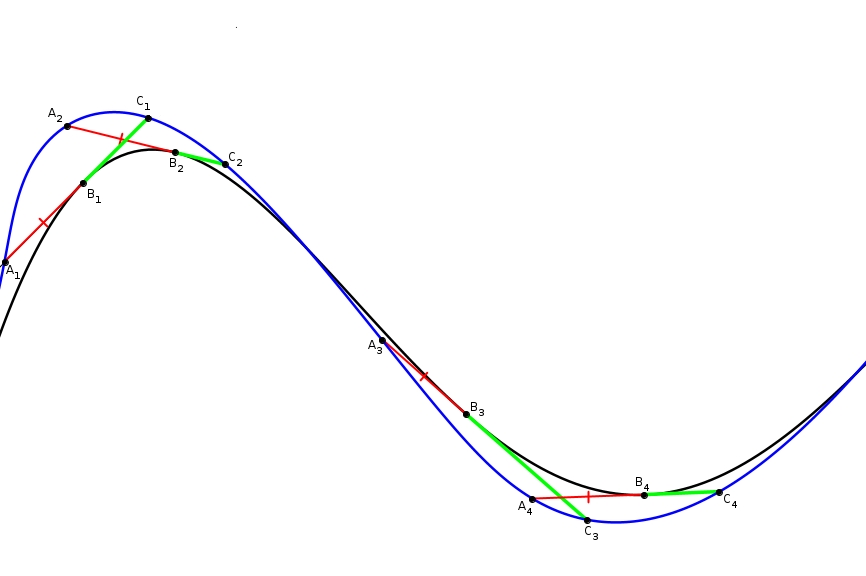
La distance entre les \(A_{i}\) et \(B_{i}\) est constante, mais la distance entre les \(B_{i}\) et \(C_{i}\) est variable, le vélo n’a donc d’autre choix que de se promener de la droite vers gauche.