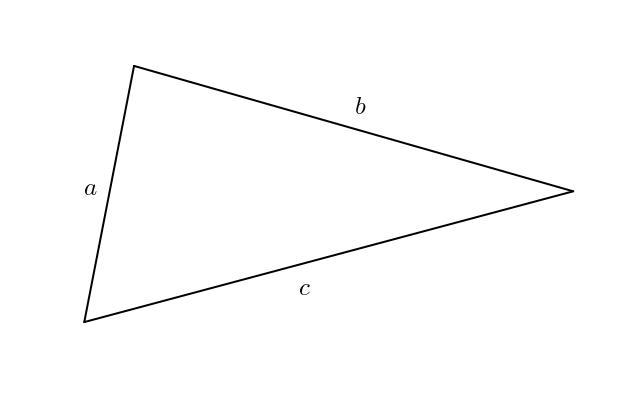
Dans un triangle, la formule de Héron nous permet de calculer l’aire du triangle avec les mesures de ses côtés. Si \(K\) est l’aire du triangle dont les côtés mesurent \(a\), \(b\) et \(c\), alors \[K = \sqrt{s\, (s-a)(s-b)(s-c)}\]dans laquelle \(s\) est le demi-périmètre \[s = \frac{a+b+c}{2}\]Nous avons rencontré la formule de Héron ici et ici. Existe-t-il une telle formule pour quadrilatère ? En d’autres mots, connaissant les mesures des quatre côtés d’un quadrilatère, est-il possible de déterminer son aire et de l’exprimer à l’aide d’une formule ?
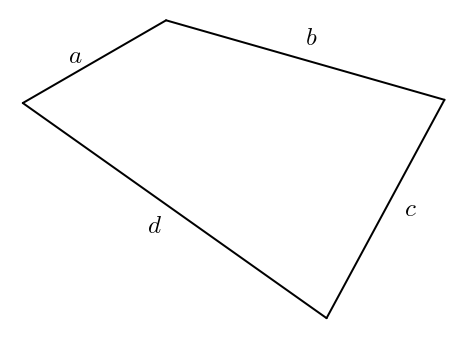
Hélas, non, ce n’est pas possible. À partir d’un quadrilatère ayant pour côtés \(a\), \(b\), \(c\) et \(d\) comme côtés, il est possible de former une infinité de quadrilatères avec les mêmes mesures de côtés. Il suffit d’imaginer des charnières aux sommets du quadrilatère. On obtient un quadrilatère articulé.
Bon. Si ce petit billet se terminait ici, cela serait un peu ordinaire. Est-il possible de trouver quelque chose d’intéressant quand même concernant le quadrilatère, ses côtés et son aire ? Bien sûr ! Il faut cependant fixer, par exemple, les diagonales ou certains angles. Supposons que l’angle entre \(a\) et \(b\) soit \(\theta\) et que l’angle entre \(c\) et \(d\) soit \(\phi\).
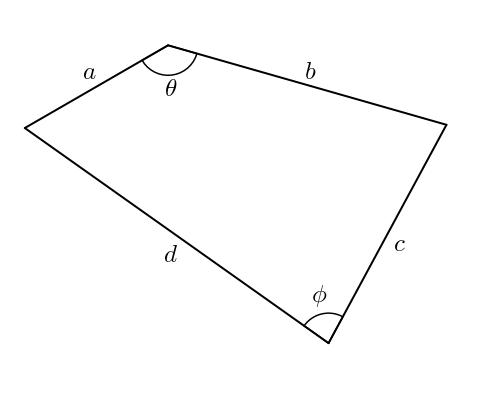
Les « charnières » ne sont plus libres de bouger. Le quadrilatère est fixe. Plus précisément, si on trace la diagonale \(x\) comme dans la figure ci-dessous, on obtient deux triangles.
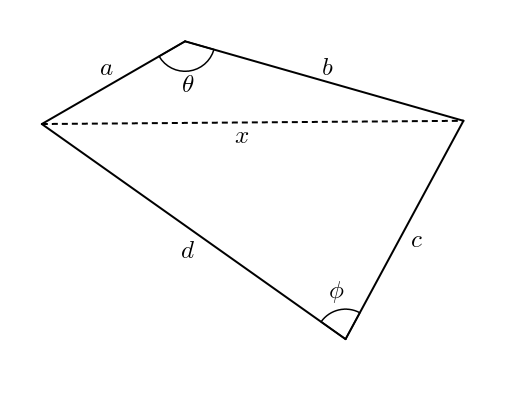
Il n’est pas très difficile ni très spectaculaire d’obtenir une expression pour l’aire du quadrilatère. Il suffit de faire la somme des aires des deux triangles. La formule d’aire trigonométrique du triangle nous donne l’expression recherchée instantanément.
\[K = \frac{ab\sin(\theta)}{2} + \frac{cd\sin(\phi)}{2}\]
Cela reste tout de même un peu décevant et c’est pourquoi, chers lecteurs, je vous invite à suivre ces quelques étapes algébriques et trigonométriques supplémentaires.
La formule de Bretschneider
\[K = \frac{ab\sin(\theta)}{2} + \frac{cd\sin(\phi)}{2}\]
On double,
\[2K = ab\sin(\theta) + cd\sin(\phi)\]
et on élève au carré, \[4K^{2} = a^{2}b^{2}\sin^{2}(\theta) + 2abcd\sin(\theta)\sin(\phi) + c^{2}d^{2}\sin^{2}(\phi)\]
et on quadruple
\[16K^{2}= 4\left( a^{2}b^{2}\sin^{2}(\theta) + 2abcd\sin(\theta)\sin(\phi) + c^{2}d^{2}\sin^{2}(\phi)\right)\]
D’autre part, en utilisant la loi des cosinus deux fois, une fois dans chaque triangle,
\[x^{2} = a^{2} + b^{2}-2ab\cos(\theta)\] et \[x^{2} = c^{2}+d^{2}-2cd\cos(\phi)\]
on obtient \[a^{2} + b^{2}-2ab\cos(\theta) = c^{2}+d^{2}-2cd\cos(\phi)\]
On peut réarranger les termes pour obtenir \begin{align*}a^{2}+b^{2}-c^{2}-d^{2}&=2ab\cos(\theta)-2cd\cos(\phi) \\ \\ a^{2}+b^{2}-c^{2}-d^{2}&=2\left(ab\cos(\theta)-cd\cos(\phi)\right)\end{align*}
En élevant au carré et en regroupant les termes du même côté de l’égalité, on obtient
\begin{align*}\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2}&=\left(2\left(ab\cos(\theta)-cd\cos(\phi)\right)\right)^{2} \\ \\ \left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2}&=4\left(ab\cos(\theta)-cd\cos(\phi)\right)^{2} \\ \\ 0&=4\left(ab\cos(\theta)-cd\cos(\phi)\right)^{2}-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2} \\ \\ &= 4\left(a^{2}b^{2}\cos^{2}(\theta)-2abcd\cos(\theta)\cos(\phi)+c^{2}d^{2}\cos^{2}(\phi)\right)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2}\end{align*}
Il est ensuite possible d’additionner ces deux équations. On obtient
\begin{align*}16K^{2}&=4\left( a^{2}b^{2}\sin^{2}(\theta) + 2abcd\sin(\theta)\sin(\phi) + c^{2}d^{2}\sin^{2}(\phi)\right) \\ &\phantom{=}+4\left(a^{2}b^{2}\cos^{2}(\theta)-2abcd\cos(\theta)\cos(\phi)+c^{2}d^{2}\cos^{2}(\phi)\right)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2} \\ \\ &=4\big(a^{2}b^{2}\sin^{2}(\theta) + 2abcd\sin(\theta)\sin(\phi) + c^{2}d^{2}\sin^{2}(\phi)+a^{2}b^{2}\cos^{2}(\theta) \\ &\phantom{=}-2abcd\cos(\theta)\cos(\phi)+c^{2}d^{2}\cos^{2}(\phi)\big)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2} \\ \\ &= 4\big(a^{2}b^{2}(\sin^{2}(\theta) +\cos^{2}(\theta))+c^{2}d^{2}(\sin^{2}(\phi) + \cos^{2}(\phi))\\ &\phantom{=}-2abcd(\cos(\theta)\cos(\phi)-\sin(\theta)\sin(\phi)\big)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2} \\ \\ &=4\left(a^{2}b^{2}+c^{2}d^{2}-2abcd\cos(\theta+\phi)\right)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2} \\ \\ &=4\left(a^{2}b^{2}+c^{2}d^{2}\right)-8abcd\cos(\theta+\phi)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2}\end{align*}en utilisant, à l’avant-dernière étape \[\sin^{2}(x) + \cos^{2}(x) = 1\]et \[\cos(x + y) = \cos(x)\cos(y)-\sin(x)\sin(y)\]On note au passage que le choix de \(\theta\) et \(\phi\) comme étant les angles entre \(a\) et \(b\) et entre \(c\) et \(d\) plutôt que les angles entre \(a\) et \(d\) et \(b\) et \(c\) n’a pas d’importance. Puisque la somme des mesures des angles intérieurs d’un quadrilatère est \(360^{\circ}\), si les angles entre les côtés \(a\) et \(d\) et \(b\) et \(c\) sont respectivement \(\alpha\) et \(\beta\), on a \[(\theta + \phi) + (\alpha + \beta) = 360^{\circ}\] ce qui implique \[\cos(\theta + \phi) = \cos(\alpha + \beta)\]Cela étant dit, à \[16K^{2}=4\left(a^{2}b^{2}+c^{2}d^{2}\right)-8abcd\cos(\theta+\phi)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2}\]on ajoute et retranche ensuite \(8abcd\) à droite et on factorise le trinôme carré parfait. On obtient \begin{align*}16K^{2} &= 4\left(a^{2}b^{2}+c^{2}d^{2}\right)+8abcd-8abcd-8abcd\cos(\theta+\phi)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2} \\ \\ &=4\left(a^{2}b^{2}+2abcd+c^{2}d^{2}\right)-8abcd\left(1+\cos(\theta+\phi)\right)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2} \\ \\ &=4\left(ab+cd\right)^{2}-8abcd\left(1+\cos(\theta+\phi)\right)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2}\end{align*}Sachant que \begin{align*}1+\cos(x)&=1+\cos\left(\frac{x}{2}+\frac{x}{2}\right) \\ \\ &=1 + \cos\left(\frac{x}{2}\right)\cos\left(\frac{x}{2}\right)-\sin\left(\frac{x}{2}\right)\sin\left(\frac{x}{2}\right) \\ \\ &=1+\cos^{2}\left(\frac{x}{2}\right)-\sin^{2}\left(\frac{x}{2}\right) \\ \\ &=1+\cos^{2}\left(\frac{x}{2}\right)-\left(1-\cos^{2}\left(\frac{x}{2}\right)\right) \\ \\ &=2\cos^{2}\left(\frac{x}{2}\right)\end{align*}on peut poser \(x = \theta + \phi\) et l’équation devient \begin{align*}16K^{2}&= 4\left(ab+cd\right)^{2}-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right)-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2} \\ \\ &= 4\left(ab+cd\right)^{2}-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2}-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right)\end{align*}Suivent quelques étapes algébriques élémentaires dans lesquelles on factorise des différences de carrés et des trinômes carrés parfaits.\begin{align*}16K^{2}&=4\left(ab+cd\right)^{2}-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2}-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right) \\ \\ &=\left(2ab+2cd\right)^{2}-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)^{2}-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right)\\ \\ &=\left(2ab+2cd-\left(a^{2}+b^{2}-c^{2}-d^{2}\right)\right)\left(2ab+2cd+\left(a^{2}+b^{2}-c^{2}-d^{2}\right)\right)-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right) \\ \\ &=\left(c^{2}+2cd+d^{2}-\left(a^{2}-2ab+b^{2}\right)\right)\left(a^{2}+2ab+b^{2}-\left(c^{2}-2cd+d^{2}\right)\right)-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right) \\ \\ &=\left(\left(c+d\right)^{2}-\left(a-b\right)^{2}\right)\left(\left(a+b\right)^{2}-\left(c-d\right)^{2}\right)-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right) \\ \\ &=\left(c+d-(a-b)\right)\left(c+d+(a-b)\right)\left(a+b-(c-d)\right)\left(a+b+(c-d)\right)-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right)\\ \\ &=\left(b+c+d-a\right)\left(a+c+d-b\right)\left(a+b+d-c\right)\left(a+b+c-d\right)-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right)\end{align*}
Il ne reste que quelques étapes simples. On introduit le demi périmètre \(s\) : \[s = \frac{a+b+c+d}{2}\]On obtient enfin \begin{align*}16K^{2}&=\left(b+c+d-a\right)\left(a+c+d-b\right)\left(a+b+d-c\right)\left(a+b+c-d\right)-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right) \\ \\ &= (2)\left(\frac{b+c+d-a}{2}\right)(2)\left(\frac{a+c+d-b}{2}\right)(2)\left(\frac{a+b+d-c}{2}\right)(2)\left(\frac{a+b+c-d}{2}\right)-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right) \\ \\ &=16\left(\frac{a+b+c+d}{2}-\frac{2a}{2}\right)\left(\frac{a+b+c+d}{2}-\frac{2b}{2}\right)\left(\frac{a+b+c+d}{2}-\frac{2c}{2}\right)\left(\frac{a+b+c+d}{2}-\frac{2d}{2}\right)-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right) \\ \\ &=16\left(s-a\right)\left(s-b\right)\left(s-c\right)\left(s-d\right)-16abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right) \end{align*}En divisant par \(16\) et en retenant la racine positive, on obtient \[K = \sqrt{\left(s-a\right)\left(s-b\right)\left(s-c\right)\left(s-d\right)-abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right)}\]La formule de Bretschneider. Voilà !
Formule de Brahmagupta
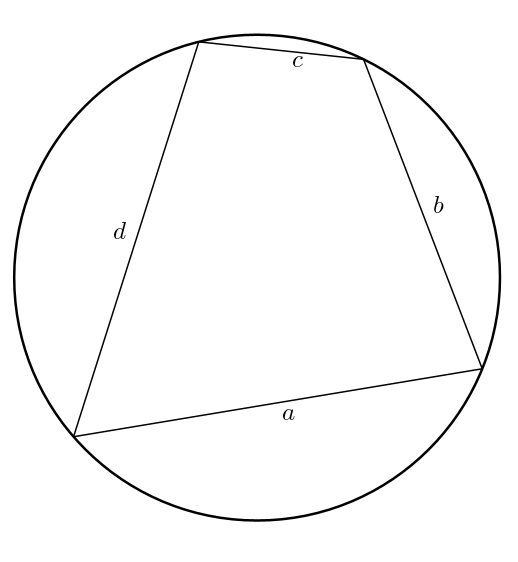
En bonus ! La formule de Bretschneider se simplifie dans le cas d’un quadrilatère inscriptible (voir la toute fin de ce billet). En effet, dans un tel quadrilatère, les angles opposés sont supplémentaires. On a \(\theta + \phi = 180^{\circ}\) ce qui fait \begin{align*}\cos^{2}\left(\frac{\theta + \phi}{2}\right) &= \cos^{2}\left(\frac{180^{\circ}}{2}\right) \\ \\ &=\cos^{2}\left(90^{\circ}\right) \\ \\ &=0\end{align*}et \[K = \sqrt{\left(s-a\right)\left(s-b\right)\left(s-c\right)\left(s-d\right)-abcd\cos^{2}\left(\frac{\theta+\phi}{2}\right)}\]devient \[K = \sqrt{(s-a)(s-b)(s-c)(s-d)}\]toujours avec \[s = \frac{a+b+c+d}{2}\]
Formule de Héron
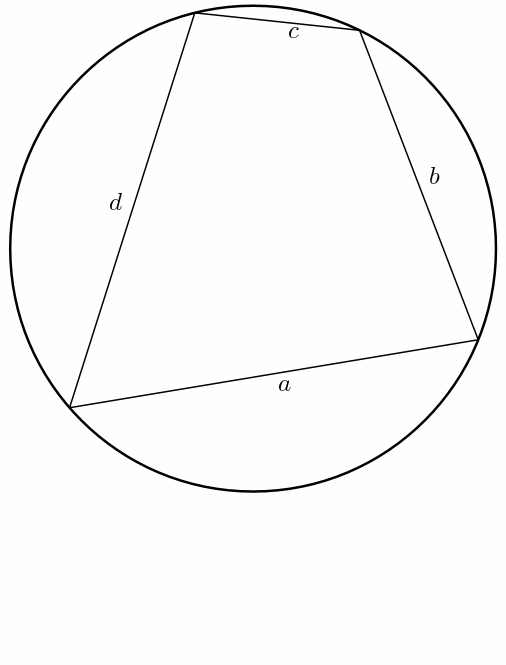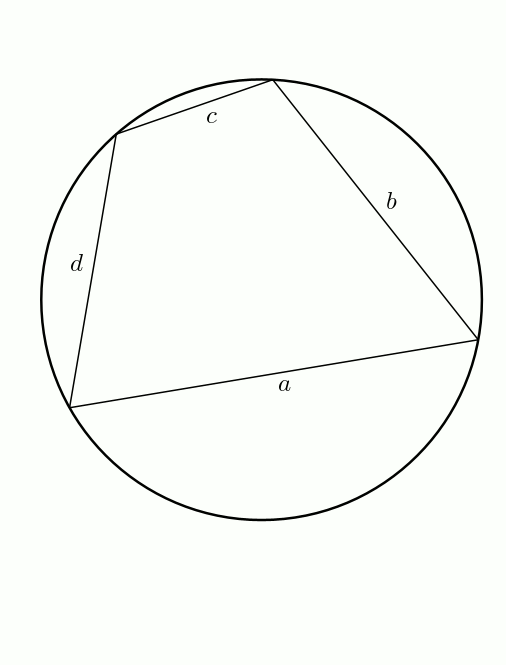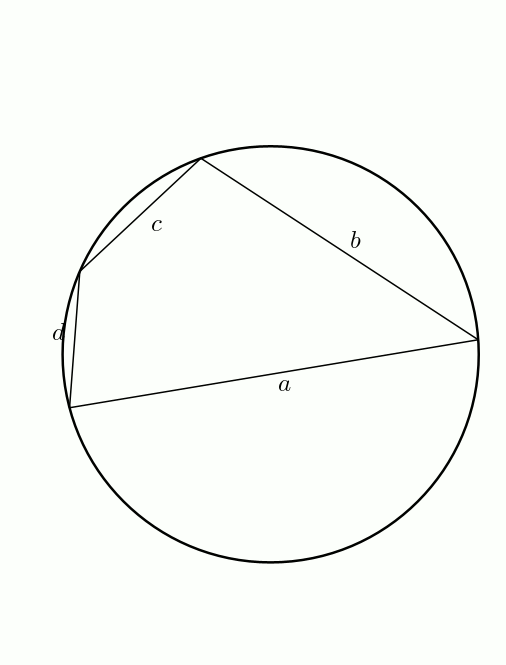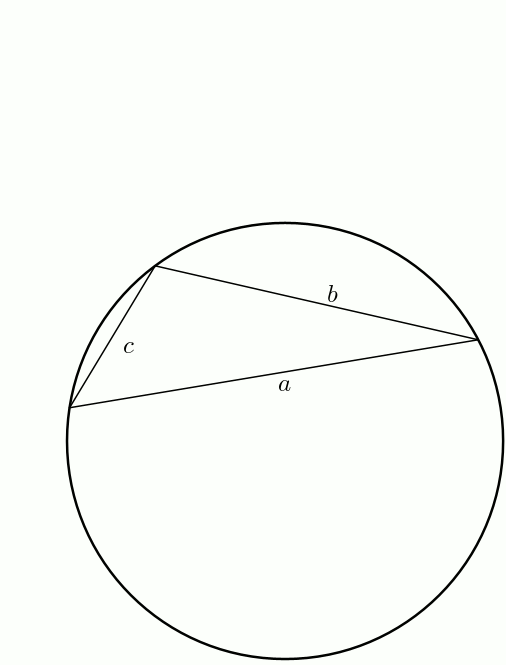
En bonus (bis) ! On peut obtenir facilement la formule de Héron à partir de celle de Brahmagupta. En effet, à partir d’un quadrilatère inscriptible, on fait tendre \(d\) vers \(0\). Le demi-périmètre \[s = \frac{a+b+c+d}{2}\] tend vers \[s = \frac{a+b+c}{2}\] et l’aire du quadrilatère \[K = \sqrt{(s-a)(s-b)(s-c)(s-d)}\]tend bien sûr vers \[K = \sqrt{s(s-a)(s-b)(s-c)}\]Voilà !
Références :
Niven, Ivan, Maxima and Minima Without Calculus, MAA, 1981
Alsina, Claudia and Roger B. Nelsen, A Cornucopia of Quadrilaterals, AMS/MAA Press, 2020
Johnson, Roger A, Advanced Euclidean Geometry, Dover, 2007