Voici un théorème surprenant de géométrie élémentaire découvert par Frank Morley (père de Christopher Morley) autour de l’année 1904. À l’époque, Morley, professeur à l’université John Hopkins, partage son résultat avec ses étudiants dans ses cours. Il attendra cependant encore plusieurs années avant de publier sa découverte dans un (obscur) journal mathématique japonnais (1924). Bien que ce théorème ait apparemment échappé tant aux géomètres de l’Antiquité qu’à ceux responsables de la renaissance de la géométrie au XIXième siècle, il est redécouvert quelques années plus tard, à point, et présenté comme problème dans Mathesis (1908) et dans l’Educational Times (1909). Une solution, trigonométrique, est publiée dans le Mathesis alors que trois solutions sont soumises au Times : une trigonométrique et deux géométriques. Le théorème tombe ensuite dans l’oubli pendant 4 ans avant de réapparaître avec F.G. Taylor et W.L. Marr dans le The proceedings of Edinburgh Mathematical Society en tant que nouveau théorème. Des étudiants et amis de Morley entrent en contact avec Taylor et Marr pour leur faire part de sa découverte. Lorsque Taylor et Marr publient leur article, ils donnent le mérite de la découverte à Morley. Voici la première preuve de leur article, particulièrement ingénieuse, et apparemment due à W.E. Philip (1914) . C’est une preuve de type directe.
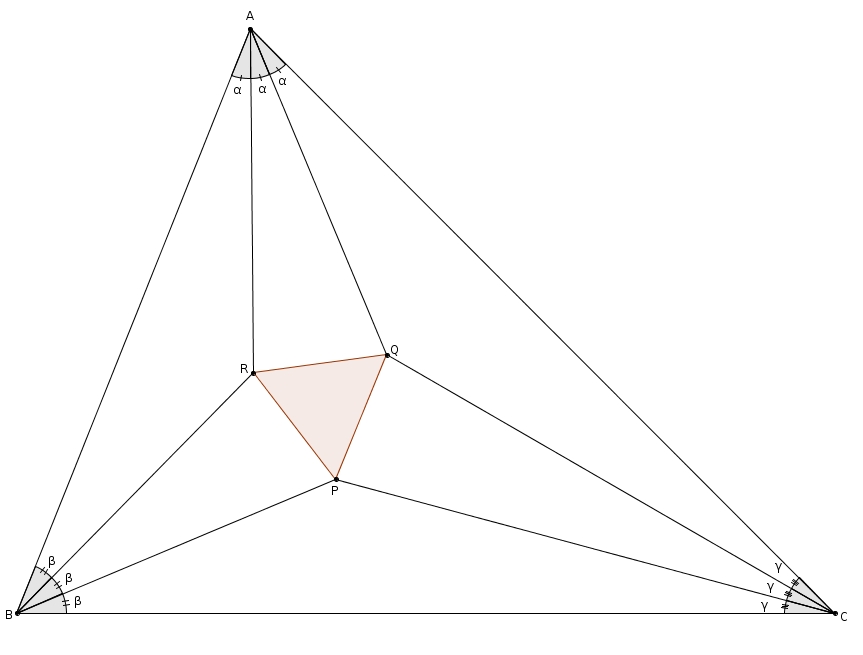
Soit un triangle ABC dont les mesures des angles sont, dans l’ordre habituel, 3α, 3β et 3γ. Les trisectrices adjacentes à BC se croisent en P, adjacentes à AC se croisent en Q et adjacentes à AB se croisent en R. On prolonge AQ et BP afin qu’elles se croisent en S. Considérons le triangle ABS : les segments AR et BR sont des bissectrices et R est donc le centre du cercle inscrit. On nomme T le point de tangence du cercle avec BS et U le point de tangence du cercle avec AS. Le prolongement de RU coupe AC en D et le prolongement de RT coupe BC en T. Enfin, de D, on mène une tangente qui touche le cercle en V (sur le petit arc TU) et coupe BS en W.
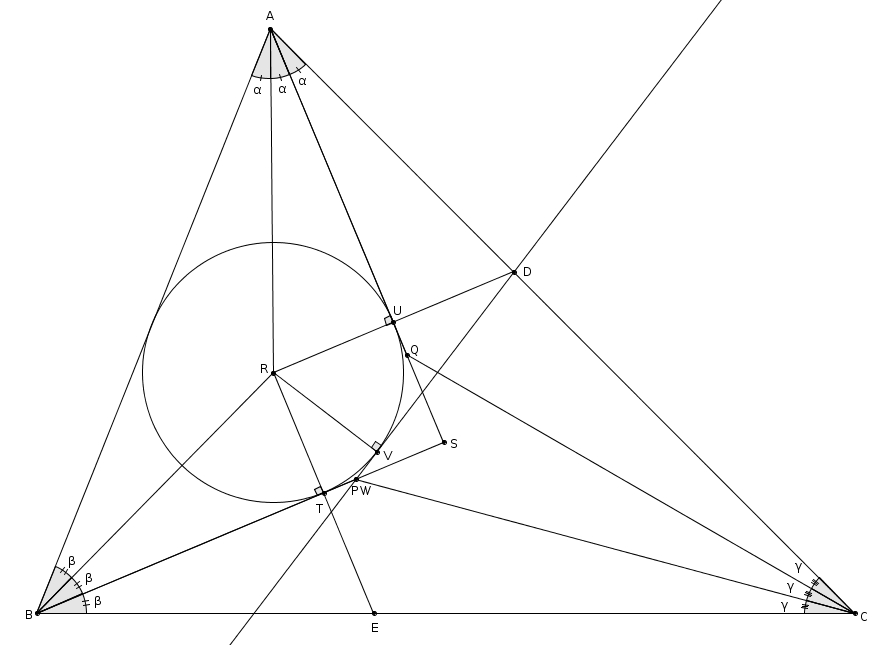
On observe d’abord que les triangles BRT et BET et les triangles ARU et ADU sont isométriques par le cas ACA. Comme RU et RT sont des rayons du cercle, on trouve, par transitivité, que les côtés RT, ET, RU et DU sont tous isométriques. Par ailleurs, la tangente DV étant perpendiculaire au rayon RV, on est en présence d’un triangle rectangle RVD dont l’hypoténuse RD est le double de la cathète RT. L’angle RDV a donc pour mesure 30° et VRD a donc pour mesure 60°.
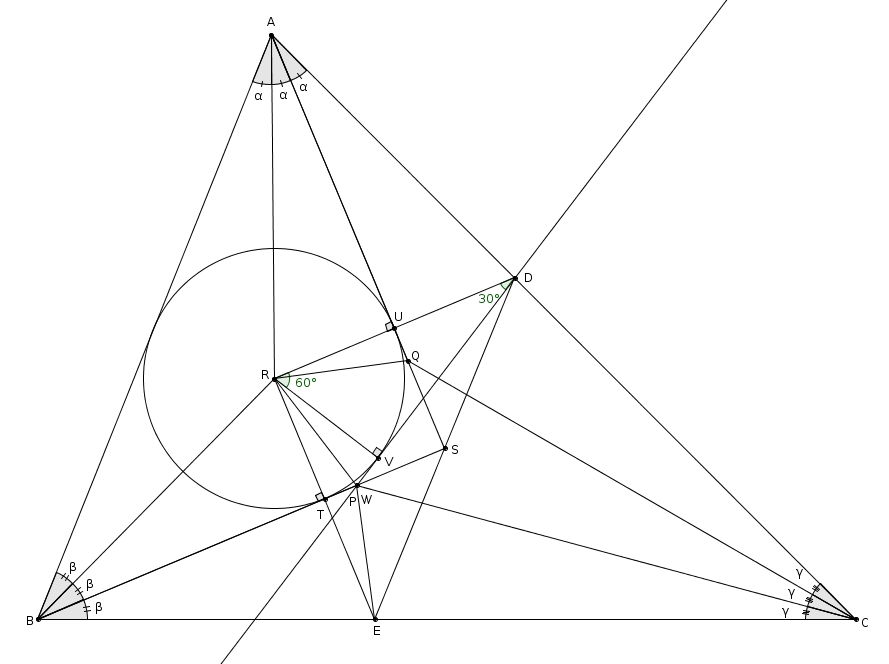
On considère maintenant le quadrilatère RUST. En soustrayant les angles droits RUS et RTS, on obtient l’égalité suivante
ou de manière équivalente
L’angle TSU fait partie du triangle ABS dans lequel on a
Enfin comme dans le grand triangle ABC on a
ce qui donne en multipliant chaque côté par 2/3
on peut combiner les résultats précédents afin d’obtenir
ou
Ensuite, les segments WT et WU sont isométriques puisqu’il s’agit de deux tangentes à un cercle issue d’un même point. W est donc sur la médiatrice issue de R dans le triangle TRV. Et comme ce triangle est isocèle (RT et RV sont des rayons), cette médiatrice est aussi bissectrice. Les angles TRW et VRW sont donc isométriques. On tire
En remplaçant par la valeur trouvée pour la mesure de TRU on obtient
c’est-à-dire
Mais puisque les angles TRW et VRW sont donc isométriques, on a aussi
Comme on a dit plus haut que les segments RT et ET étaient isométriques, les triangles TRW et TEW sont isométriques par le cas CAC. Et comme dans les triangles isométriques les angles homologues sont isométriques, on a
Considérons maintenant le triangle RED. Puisque les segments RE et RD sont isométriques, le triangle est isocèle et les angles RED et RDE sont isométriques. Toujours dans le même triangle, on trouve
et comme on avait trouvé préalablement que
on a
Puisque
on trouve
et puisque
on trouve aussi
Dans le triangle WED, on a
ce qui donne en remplaçant
et donc
Puisque
c’est-à-dire que les angles EWD et ECD sont supplémentaires, le quadrilatère EWDC est inscriptible dans un cercle[1]. Les angles WDE et WCE interceptent le même arc WE et sont donc de même mesure γ. W est donc sur la trisectrice CP (et par définition il est aussi sur la trisectrice BP) et on peut conclure que W et P sont confondus.
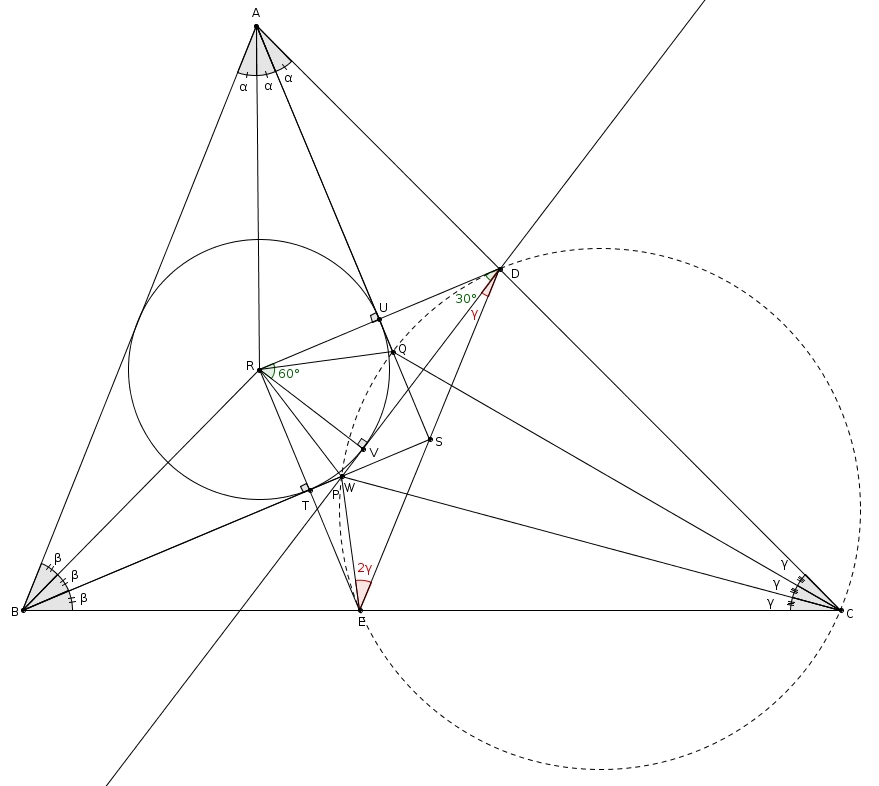
De façon similaire, on peut montrer que la tangente au cercle issue de E passe par Q. L’angle QED a donc lui aussi pour mesure γ. La figure RED est symétrique et les points P et Q sont placés de façon symétrique de part et d’autre. En particulier les segments RP et RQ sont isométriques et incidemment les triangles TRP et QRU sont isométriques. Les angles homologues TRP et QRU sont eux-aussi isométriques. Mais comme les angles TRP et PRV sont eux-mêmes isométriques, on trouve, par transitivité, que les angles PRV et QRU sont isométriques. En outre, comme l’angle VRD a pour mesure 60° et que
on a, en substituant
ce qui implique donc
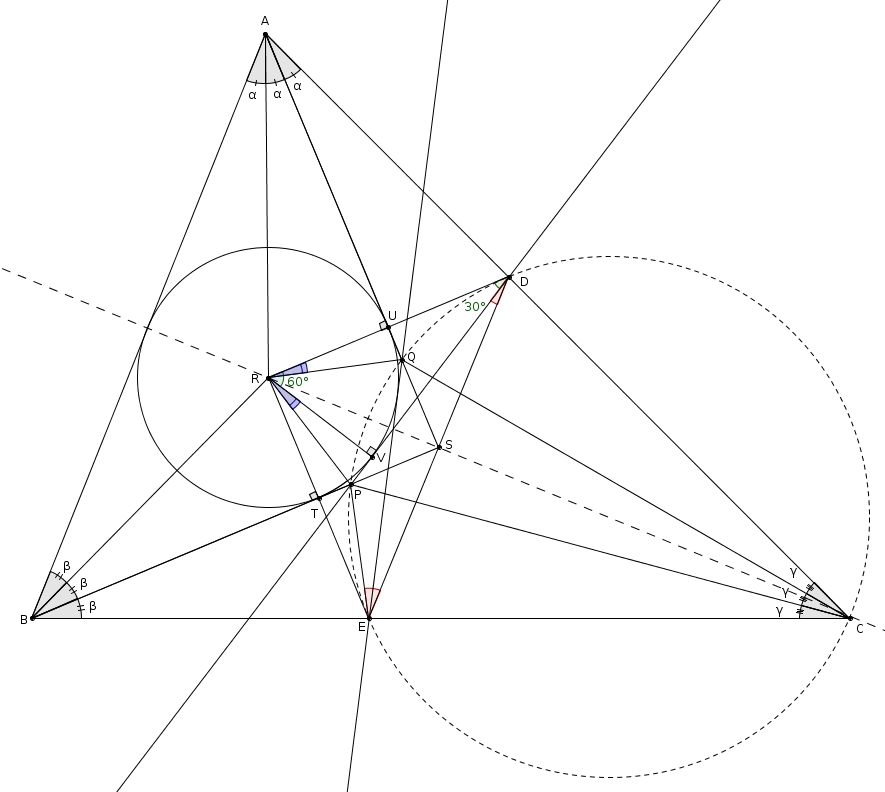
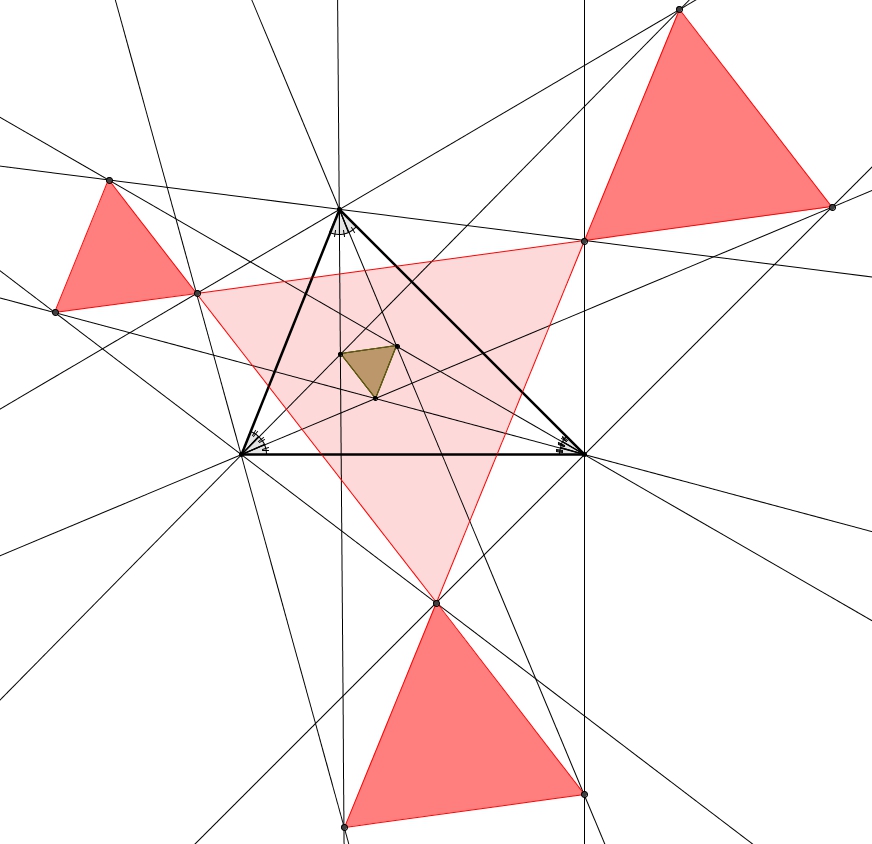
Puisqu’il nous est possible de reproduire la même démarche pour chaque sommet, le triangle PRQ est équiangle et donc équilatéral.
[1] Nous avons déjà rencontré sur ce blogue ce théorème (Proposition III.22 des Éléments d’Euclide). Si un quadrilatère ABCD est inscriptible dans un cercle, alors ses angles opposés sont supplémentaires
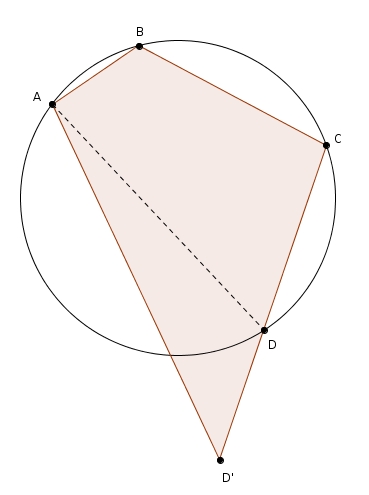
L’angle D intercepte l’arc ABC. L’angle B intercepte l’arc ADC. Ensemble, ils interceptent le cercle au complet : comme un angle inscrit a pour mesure la moitié de l’angle au centre qui intercepte le même arc, on peut conclure qu’ils sont supplémentaires. Réciproquement, si un quadrilatère possède des angles opposés supplémentaires, alors il est inscriptible. Considérons un quadrilatère ABCD’ dont les angles opposés sont supplémentaires mais qui n’est pas inscriptible. On peut tracer un cercle passant par ABC mais comme ABCD’ n’est pas inscriptible, le cercle ne passe pas par D’ (ici D’ est à l’extérieur du cercle mais il pourrait très bien être à l’intérieur). Soit D l’intersection de CD’ et du cercle (si D’ est à l’intérieur, il suffit de prolonger CD’). Par le théorème que l’on vient de prouver, les angles D et B sont supplémentaires… or par hypothèse D’ et B sont supplémentaires : il y contradiction! Il faut donc que D’ et D coïncident.
Références :
H.S.M. Coxeter and S.L. Greitzer (1967), Geometry Revisited pp 47-49
R. A. Johnson (1929), Modern Geometry pp 253-254
Toujours aussi plaisant de lire tes articles, on y apprend des choses intéressantes et très accessibles.
Je seconde Dominik. Merci.
Dominik, tu es un collègue pour qui j’ai beaucoup d’estime.
Missmath, comme vous le savez, c’est réciproque puisque je suis un avide lecteur de votre blogue !