Voici une autre démonstration de la formule de Héron, moins élégante que la première mais plus pratique. Il existe d’autres preuves plus courtes qui ont recours à la loi des cosinus et à des identités trigonométriques. La preuve qui suit à l’avantage de garder les choses simples, la relation de Pythagore et la factorisation d’un trinôme carré parfait et d’une différence de carrés étant les seuls prérequis.
La formule de Héron nous permet calculer l’aire d’un triangle en ne connaissant que la mesure de ses côtés.
Considérons un triangle quelconque \(ABC\). On trace la hauteur \(\overline{AD}\). Elle tombe perpendiculairement sur \(\overline{CD}\). Appelons \(x\) la mesure du segment \(CD\) et \(a-x\) celle du segment \(BD\). (1)
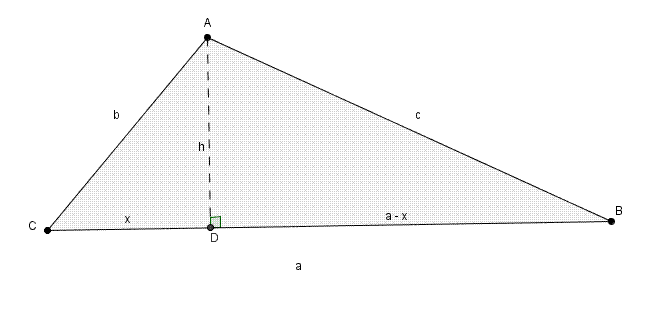On peut d’abord trouver l’aire \(K\) du triangle \[K = \frac{ah}{2}\]On élève chaque côté au carré \[K^{2}=\frac{a^{2}h^{2}}{4}\]et on réserve pour une utilisation ultérieure. Nous allons ensuite trouver une expression correspondant au carré de la hauteur et la remplacer dans l’équation ci-dessus. Les triangles \(ADC\) et \(ADB\) étant rectangles, on trouve, avec la relation de Pythagore, dans le triangle \(ADC\), \[h^{2}+x^{2}=b^{2}\]et en isolant \(h^{2}\) \[h^{2}=b^{2}-x^{2}\]et puis dans le triangle \(ADB\),\[h^{2}+(a-x)^{2}=c^{2}\]et toujours en isolant \(h^{2}\) \[h^{2}=c^{2}-(a-x)^{2}\]En développant le carré dans l’expression précédente on obtient \[h^{2}=c^{2}-\left(a^{2}-2ax+x^{2}\right)\]ou \[h^{2}=c^{2}-a^{2}+2ax-x^{2}\]Il nous est maintenant possible de comparer les deux expressions précédentes pour \(h^{2}\) \[b^{2}-x^{2}=c^{2}-a^{2}+2ax-x^{2}\]On additionne d’abord \(x^{2}\) de chaque côté afin d’obtenir \[b^{2}=c^{2}-a^{2}+2ax\]Il nous est maintenant possible d’isoler \(x\) \[a^{2}+b^{2}-c^{2}=2ax\]puis\[\frac{a^{2}+b^{2}-c^{2}}{2a}=x\]En reprenant l’équation \[h^{2}=b^{2}-x^{2}\]et en remplaçant \(x\) par l’expression que l’on vient de trouver, on obtient \[h^{2}=b^{2}-\left(\frac{a^{2}+b^{2}-c^{2}}{2a}\right)^{2}\]L’expression de droite est une différence de carrés. En factorisant on obtient \[h^{2}=\left(b+\frac{a^{2}+b^{2}-c^{2}}{2a}\right)\left(b-\frac{a^{2}+b^{2}-c^{2}}{2a}\right)\]En mettant sur dénominateur commun dans les deux parenthèses on obtient\begin{align*}h^{2}&=\left(\frac{2ab}{2a}+\frac{a^{2}+b^{2}-c^{2}}{2a}\right)\left(\frac{2ab}{2a}-\frac{a^{2}+b^{2}-c^{2}}{2a}\right) \\ \\ &=\left(\frac{a^{2}+2ab+b^{2}-c^{2}}{2a}\right)\left(\frac{-a^{2}+2ab-b^{2}+c^{2}}{2a}\right)\end{align*}On effectue ensuite la mise en évidence de \((-1)\) dans la deuxième parenthèse. On obtient alors \[h^{2}=(-1)\left(\frac{a^{2}+2ab+b^{2}-c^{2}}{2a}\right)\left(\frac{a^{2}-2ab+b^{2}-c^{2}}{2a}\right)\]Les trois premiers termes au numérateur dans les deux parenthèses sont des trinômes carrés parfaits. En factorisant on obtient\[h^{2}=(-1)\left(\frac{\left(a+b\right)^{2}-c^{2}}{2a}\right)\left(\frac{\left(a-b\right)^{2}-c^{2}}{2a}\right)\]Et on se retrouve à nouveau avec des différences de carrés. En factorisant ces deux différences de carrés on obtient \[h^{2}=(-1)\left(\frac{\left(a+b+c\right)\left(a+b-c\right)}{2a}\right)\left(\frac{\left(a-b+c\right)\left(a-b-c\right)}{2a}\right)\]ce qui donne en multipliant \[h^{2}=(-1)\left(\frac{\left(a+b+c\right)\left(a+b-c\right)\left(a-b+c\right)\left(a-b-c\right)}{4a^{2}}\right)\]On distribue ensuite commodément le \((-1)\) sur le dernier facteur \[h^{2}=\frac{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}{4a^{2}}\]La formule de Héron exprimant l’aire avec le demi-périmètre s, nous allons maintenant introduire cette quantité \[s=\frac{a+b+c}{2}\]En multipliant par \(2\) on obtient \[2s = a+b+c\]puis successivement, en soustrayant d’abord \(2a\), puis \(2b\) puis \(2c\) \begin{align*}2s-2a&=-a+b+c \\ \\ 2s-2b &= a-b+c \\ \\ 2s-2c &= a+b-c\end{align*}En reprenant\[h^{2}=\frac{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}{4a^{2}}\]on substitue habilement \[h^{2}=\frac{(2s)(2s-2c)(2s-2b)(2s-2a)}{4a^{2}}\]On effectue ensuite des mises en évidence \[h^{2}=\frac{(2s)(2)(s-c)(2)(s-b)(2)(s-a)}{4a^{2}}\]ce qui donne d’abord en multipliant \[h^{2} = \frac{16s(s-a)(s-b)(s-c)}{4a^{2}}\]puis en simplifiant et en réarrangeant les facteurs \[h^{2}=\frac{4s(s-a)(s-b)(s-c)}{a^{2}}\]On a maintenant une expression satisfaisante du carré de la hauteur. On remplace donc dans \[K^{2}=\frac{a^{2}h^{2}}{4}\]afin d’obtenir \[K^{2}= \frac{a^{2}\cdot \frac{4s(s-a)(s-b)(s-c)}{a^{2}}}{4}\]Il est possible de simplifier les \(a^{2}\) \[K^{2}= \frac{4s(s-a)(s-b)(s-c)}{4}\]puis les \(4\) au numérateur et dénominateur\[K^{2}=s(s-a)(s-b)(s-c)\]Il suffit finalement d’extraire la racine carrée (positive, puisqu’il s’agit de l’aire) afin d’obtenir l’expression recherchée \[K=\sqrt{s(s-a)(s-b)(s-c)}\]
(1) La démarche fonctionne aussi lorsque la hauteur tombe sur le prolongement de \(BC\) et non sur \(BC\) même (donc à l’extérieur du triangle). Le segment \(BD\) devient \(a+x\)