Le regretté Samuel L. Greitzer détestait, apparament, ce qu’on appelle les « mathématiques modernes ». Il était farouchement opposé à l’idée d’inclure dans les olympiades mathématiques des problèmes de menteurs et diseurs de vérité (liars and truthtellers), de diagrammes de Venn ou d’arithmétique dans des bases autres que la base 10. Son ami Stanley Rabinowitz lui proposa donc, à la blague, ce problème :
Alice et Bob vivent tous les deux dans la petite principauté de Binuméria. Les habitants de Binuméria parlent tous exclusivement le français et disent tous la vérité, toujours. Cependant, ils utilisent deux systèmes de numération et, traditionnellement, lorsqu’ils parlent, les habitants de Binuméria ne changent jamais de base de numération dans une même phrase. Alice dit : « Je suis une grande adepte de la base 10 et je ne parle que dans cette base. Dans la principauté de Binuméria, 26 personnes savent compter en base 10 et seulement 22 personnes savent compter en base 14 ». Bob ajoute ensuite : « Des 25 résidents de la principauté, 13 sont numériquement bilingues et 1 seul ne sait compter, il est numériquement analphabète ». Combien de personnes vivent dans la principauté de Binuméria ?
Voyons voir. Bien sûr, Alice ne parle probablement pas en base dix (notre bonne vieille base décimale) parce que, rappelez-vous, toutes les bases sont des bases 10.

Ainsi, si la base d’Alice est \(a\), alors il y a\[2a+6\]personnes qui peuvent compter, comme elle, en base \(a\). Il y a aussi \[2a + 2\]personnes qui savent compter dans l’autre base, disons la base \(b\). Or, comme Alice dit : « la base 14 », et que le « 14 » est exprimé en base \(a\), on trouve que la base \(b\) correspond en fait à \[a + 4\]Bob parle dans cette autre base, puisqu’il dit qu’il y a « 25 » résidents au total, alors qu’Alice comptait déjà « 26 » personnes et ça, rien que pour sa propre base. On déduit même que la base qu’utilise Bob est plus grande que celle d’Alice. Ainsi Bob utilise la base \[b = a + 4\]Toujours selon Bob, il y a \begin{align*}2b+5&=2(a+4)+5\\ \\ &=2a+13\end{align*}résidents au total et de ce nombre,\begin{align*}b+3&=(a+4)+3 \\ \\ &=a+7\end{align*}sont bilingues. On a donc d’abord
Il reste\[2a+6-(a+7)=a-1\]personnes parlant exclusivement en base \(a\) et de la même manière\[2a + 2-(a+7)=a-5\]personnes parlant exclusivement en base \(b\).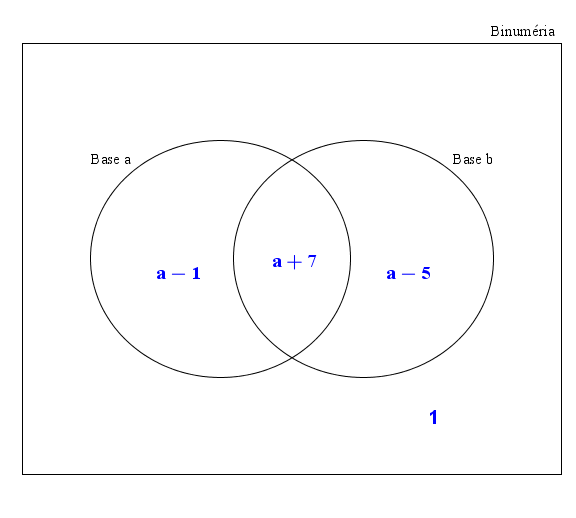 On peut donc trouver la valeur de \(a\) en faisant la somme des habitants de Binuméria à partir des différentes régions du diagramme de Venn ci-dessus\[(a-1)+(a+7)+(a-5)+1=3a+2\]Cette expression représente le même nombre que le total déjà annoncé par Bob \[3a + 2 = 2a + 13\]ce qui nous donne la base d’Alice \[a = 11\]et aussi la base de Bob\begin{align*}b&=a+4 \\ \\ &=11+4 \\ \\ &=15\end{align*}On peut enfin répondre à la question ! Il y a \[2(11)+13=2(15)+5 =35\]personnes qui vivent à Binuméria !
On peut donc trouver la valeur de \(a\) en faisant la somme des habitants de Binuméria à partir des différentes régions du diagramme de Venn ci-dessus\[(a-1)+(a+7)+(a-5)+1=3a+2\]Cette expression représente le même nombre que le total déjà annoncé par Bob \[3a + 2 = 2a + 13\]ce qui nous donne la base d’Alice \[a = 11\]et aussi la base de Bob\begin{align*}b&=a+4 \\ \\ &=11+4 \\ \\ &=15\end{align*}On peut enfin répondre à la question ! Il y a \[2(11)+13=2(15)+5 =35\]personnes qui vivent à Binuméria !
Référence : Joseph D. E. Konhauser, Dan Velleman, Stan Wagon, (1996) Which Way Did the Bicycle Go?