Tu as ta règle ? Alors pas de problème ! Sur chacun des côtés de l’angle, marque un trait à \(60\) millimètres du sommet. Mesure ensuite la distance en millimètres entre les traits et voilà ! Tu as (une approximation parfaitement acceptable de) la mesure de ton angle en degrés ! Génial ?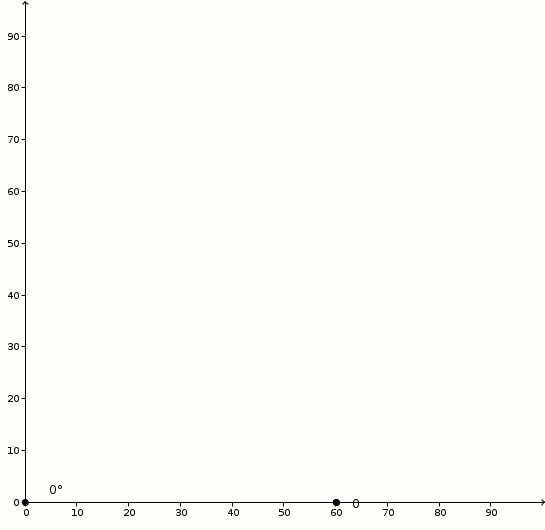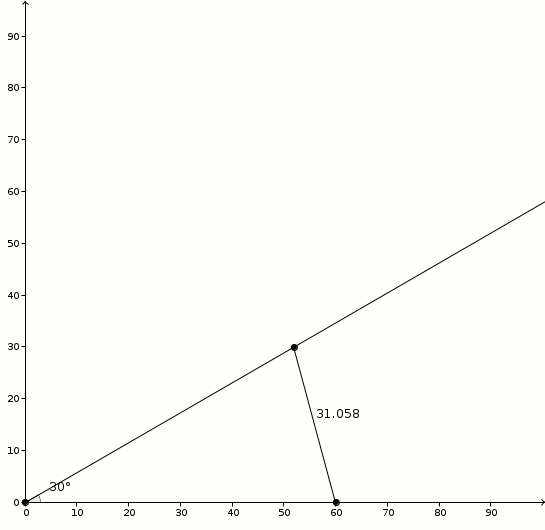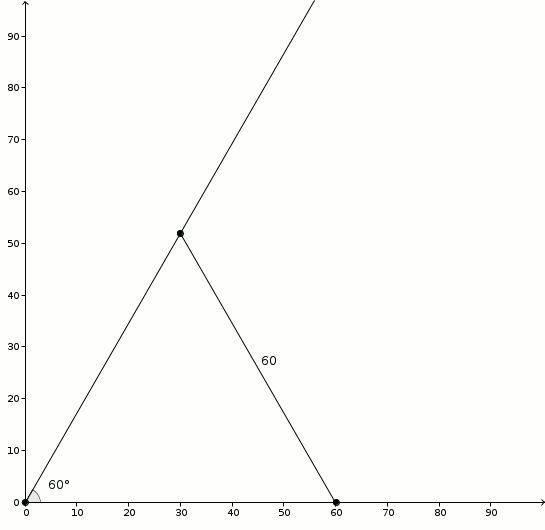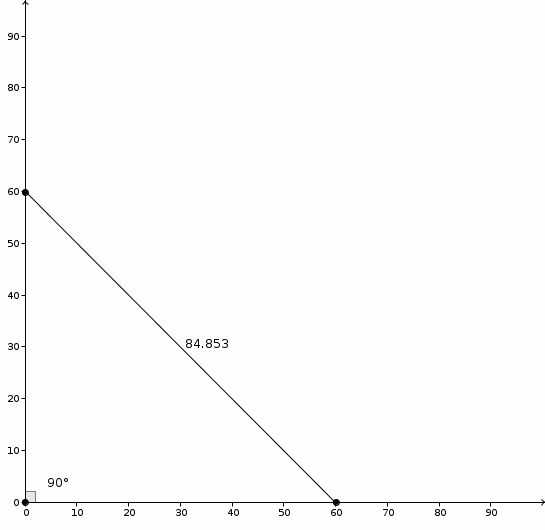
Pourquoi est-ce que ça fonctionne ? On considère un angle \(\alpha\) et on procède tel qu’indiqué. En marquant les côtés de l’angle à la même distance (ici, \(60\) millimètres), on dessine un triangle isocèle. Et comme c’est un triangle isocèle, la bissectrice de l’angle \(\alpha\) sera aussi une médiatrice.
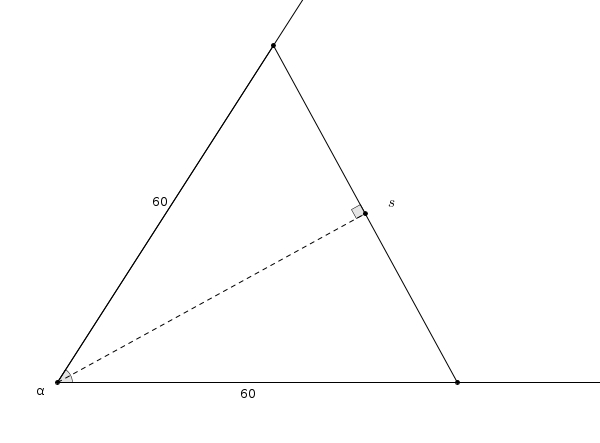Ainsi, en n’oubliant pas que \[1^{\circ} = \frac{\pi}{180}\]on observe la relation suivante dans les triangles rectangles formés par la bissectrice/médiatrice \[\sin\left(\frac{\pi}{180}\cdot \frac{\alpha}{2}\right) = \frac{\frac{s}{2}}{60}\]et dans laquelle \(\alpha\) est exprimé en degrés. De \[\sin\left(\frac{\pi}{360}\alpha\right) = \frac{s}{120}\]on utilise maintenant deux approximations si grossières qu’elles vous feront perdre, peut-être, tout espoir d’obtenir une expression utile au final. Et pourtant ! D’abord, pour de petits angles (exprimés en radian), on a \[\sin\left(\theta\right) \approx \theta\]ce qui donne comme première approximation \[\frac{\pi}{360} \approx \frac{s}{120}\]et en utilisant (ma parole !) \[\pi \approx 3\]on obtient ensuite \[\frac{3}{360} \alpha \approx \frac{s}{120}\]C’est donc avec un certain scepticisme qu’on retrouve effectivement \[\alpha \approx s\]Est-ce que l’approximation est fiable ? Le graphique suivant montre la relation entre \(\alpha\) (abscisses) et \(\alpha-s\) (ordonnées).
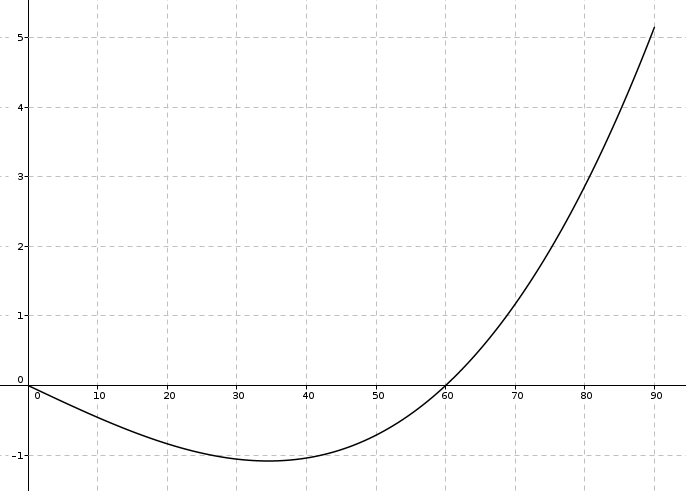On remarque que pour des angles entre \(0^{\circ}\) et (environ) \(75^{\circ}\), l’erreur est de moins de \(2^{\circ}\). Pas mal ! Après \(75^{\circ}\), ça se gâte un peu, et l’erreur culmine avec un maximum d’environ \(5^{\circ}\) lorsque l’angle est près d’un angle droit. Cependant, toutes proportions gardées, l’erreur de \(5^{\circ}\) reste quand même relativement petite pour cette approximation très économique.
On peut se demander si \(60\) a quelque chose de particulier, s’il existe des mesures qui donnent de meilleures approximations. En marquant l’angle à \(62\) millimètres au lieu de \(60\), on semble améliorer les choses : on s’assure que l’erreur maximale ne dépasse pas environ \(2,\!4^{\circ}\) (au lieu d’un peu plus de \(5^{\circ}\) comme c’est le cas ici avec \(60\) millimètres). Bien que \(62\) millimètres offrent une meilleure garantie sur l’erreur maximale (qu’importe l’angle, c’est moins de \(2,\!4^{\circ}\)), on se rend compte que la plupart des angles sont moins précis en utilisant cette mesure. En d’autres mots, avec \(62\) millimètres, l’erreur maximale est plus petite mais l’erreur moyenne est plus grande. En fait, la mesure qui offre la plus petite erreur moyenne est… \(60\) millimètres. Excellent.
En gardant notre mesure de \(60\) millimètres pour minimiser l’erreur moyenne, peut-on améliorer notre approximation sans trop compliquer les choses ? Kowalski [1], dans son article, propose d’utiliser une règle simple : en bas de \(60^{\circ}\), on soustrait \(1\), en haut de \(60^{\circ}\) on ajoute \(2,\!5\). \[\text{Approx} =\begin{cases} s-1 & \text{ si } \alpha<60^{\circ} \\ s & \text{ si } \alpha = 60^{\circ} \\ s+2,\!5 & \text{ si } \alpha>60^{\circ}\end{cases}\]
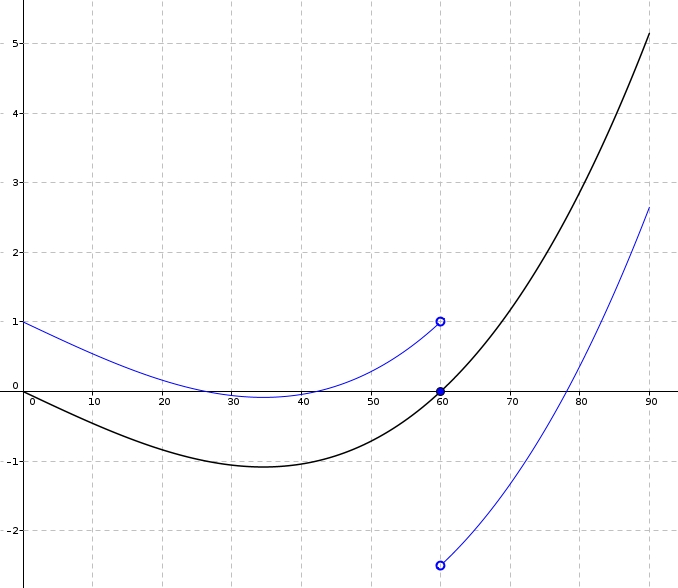
En bleu, α – s avec ajustement.
Référence : [1] Travis Kowalski, College Mathematics Journal, Volume 39, Number 4, September 2008 , pp. 273-279