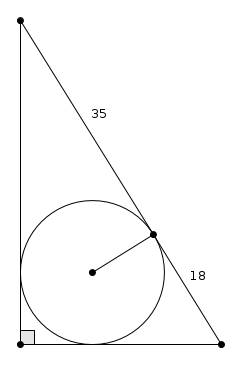
Le problème était le suivant :
Trouvez l’aire du triangle rectangle ci-dessus (le cercle est inscrit)
La démarche attendue était à peu près celle-ci. Comme les tangentes à un cercle issues d’un même point sont de même longueur, on trouve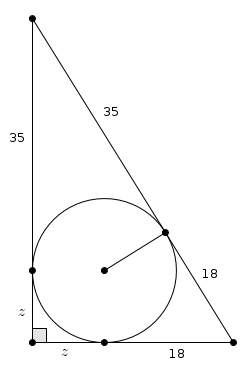
ce qui nous permet d’établir une équation avec Pythagore.\[\left(z + 35\right)^{2} + \left(z + 18\right)^{2}=\left(35 + 18\right)^{2}\]En développant on obtient\[z^{2} + 70z + 1\,225 + z^{2} + 36z + 324 = 2\,809\]puis en regroupant les termes semblables\[2z^{2} + 106z-1\,260=0\]et enfin en divisant par 2, on trouve un trinôme du deuxième degré\[z^{2}+53z-630=0\]qui, ô joie, se factorise assez facilement\[\left(z-10\right)\left(z+63\right)=0\]La seule solution sensée pour notre problème est donc\[z=10\]et l’aire du triangle rectangle doit être\[A_{\text{triangle}} = \frac{\left(35 + 10\right)\left(18+10\right)}{2}=\frac{45\cdot28}{2} = 630\]Hummmm ! Or, \[35 \times 18 = 630\]Hasard ? Oh ! Je ne pense pas ! Il suffit de construire un rectangle à l’aide d’un deuxième triangle isométrique au premier (il existe des preuves algébriques assez simple mais on préfère la très élégante preuve géométrique suivante)
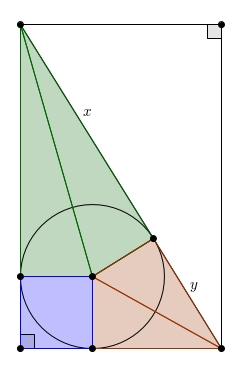 et de réarranger un triangle vert et un triangle rouge de manière à obtenir un rectangle équivalent au triangle initial,
et de réarranger un triangle vert et un triangle rouge de manière à obtenir un rectangle équivalent au triangle initial,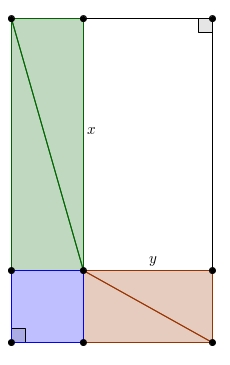 un rectangle d’aire \(xy\). Ainsi, l’aire d’un triangle rectangle est égal au produit \(xy\) des longueurs des segments déterminés sur l’hypoténuse par le point de tangence au cercle inscrit.
un rectangle d’aire \(xy\). Ainsi, l’aire d’un triangle rectangle est égal au produit \(xy\) des longueurs des segments déterminés sur l’hypoténuse par le point de tangence au cercle inscrit.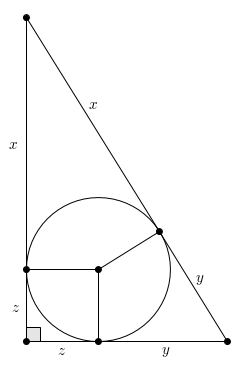
Comment construire d’autres exemples (avec des nombres entiers) ? L’exemple du début de l’article était-il difficile à construire, était-il rare ? La réponse est non. On sait comment générer des triplets pythagoriciens, et, sans devoir s’en tenir aux triplets primitifs, il suffit de choisir \(a>b\) entiers et poser\begin{align*}x+z&=a^{2}-b^{2}\\ \\ y+z&=2ab \\ \\ x+y&=a^{2}+b^{2}\end{align*}En soustrayant la deuxième équation à la première on obtient\[x-y=a^{2}-2ab-b^{2}\]et en additionnant cette dernière équation à la troisième on obtient\[2x=2a^{2}-2ab\]ou\[x=a^{2}-ab\]Cette expression pour \(x\) nous permet de trouver l’expression pour \(y\) \[y=b^{2}+ab\]et pour \(z\) \[z=ab-b^{2}\]L’exemple du début de l’article a donc été construit en choisissant \(a=7\) et \(b=2\).
Référence : Claudi Alsina et Roger B. Nelsen (2013), Charming Proofs: A Journey into Elegant Mathematics