De combien de manière différentes peut-on faire des piles avec \(n\) objets identiques si l’ordre des piles est important ?
Par exemple, il y a 8 façons de faire des piles avec 4 objets identiques.
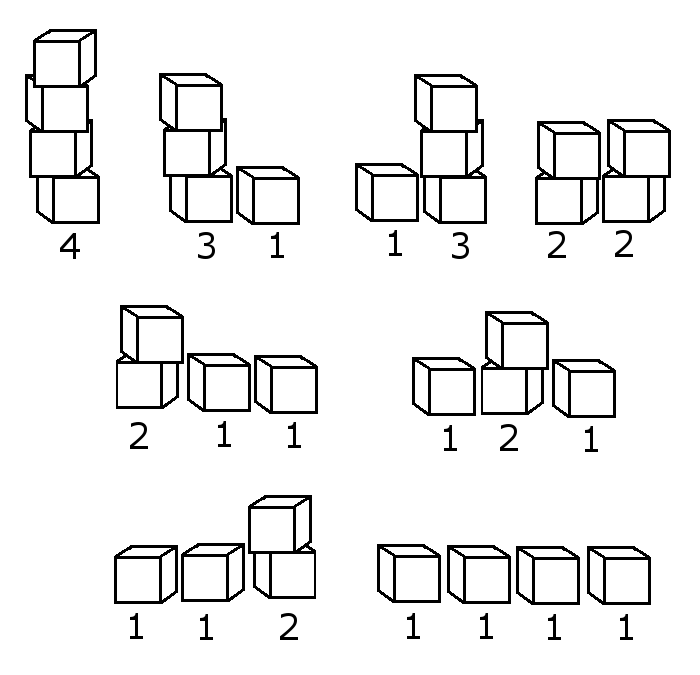
On peut représenter de manière plus abstraite mais aussi plus efficacement ces huit façons grâce aux sommes suivantes : \begin{align*}&4 &&3 + 1 &&&1 + 3 &&&&2 + 2 \\ \\ &2 + 1 + 1 &&1 + 2 + 1 &&&1 + 1 + 2 &&&&1 + 1 + 1 + 1\end{align*}
Le problème se reformule ainsi : de combien de façons différentes peut-on exprimer un nombre \(n\) comme une somme de nombres entiers strictement positifs si l’ordre des termes est important.
Vous pouvez vous amuser à chercher les différentes sommes pour des \(n\) petits.
| Nombre d'objets identiques | Nombre de façons de faire des piles, avec ordre | Sommes correspondantes |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 1 + 1 |
| 3 | 4 | 3 1 + 3 3 + 1 2 + 2 |
| 4 | 8 | 4 1 + 3 3 + 1 2 + 2 1 + 1 + 2 1 + 2 + 1 2 + 1 + 1 1 + 1 + 1 + 1 |
| 5 | 16 | 5 1 + 4 4 + 1 2 + 3 3 + 2 1 + 2 + 3 1 + 3 + 2 2 + 1 + 3 2 + 3 + 1 3 + 1 + 2 3 + 2 + 1 1 + 1 + 1 + 2 1 + 1 + 2 + 1 1 + 2 + 1 + 1 2 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1 |
Les compositions
Comme on le constate pour de petites valeurs de \(n\), il y a toujours \(2^{n-1}\) façons de former des piles avec \(n\) objets identiques si l’ordre est important. En combinatoire, c’est ce qu’on appelle les compositions d’un nombre. En d’autres mots, si \(c(n)\) est le nombre de compositions de \(n\), alors \[c(n) = 2^{n-1}\]
Supposons qu’on représente les \(n\) objets avec des étoiles. Par exemple, considérons le cas où \(n = 5\).\[ \star \ \textcolor{White}{\vert} \ \star \! \ \textcolor{White}{\vert} \ \star \! \ \textcolor{White}{\vert} \ \star \ \textcolor{White}{\vert} \ \star\]Entre ces \(n\) étoiles, je peux aller placer \(n-1\) « séparateurs », que je représenterai avec des barres verticales. Dans ce cas-ci, il y a \(5-1 = 4\) séparateurs.\[ \star \ \textcolor{Grey}{\vert} \ \star \! \ \textcolor{Grey}{\vert} \ \star \! \ \textcolor{Grey}{\vert} \ \star \ \textcolor{Grey}{\vert} \ \star\]
Je peux décider « d’activer » ou non ces séparateurs individuellement. Cela me permet de former des groupes d’étoiles qui correspondent à des piles ou des termes de la somme. Par exemple, \[ \star \ \textcolor{Red}{\vert} \ \star \! \ \textcolor{White}{\vert} \ \star \! \ \textcolor{White}{\vert} \ \star \ \textcolor{Red}{\vert} \ \star\]correspond à \[1 + 3 + 1\] \[~\] \[~\] \[~\]
\[ \star \ \textcolor{White}{\vert} \ \star \! \ \textcolor{White}{\vert} \ \star \! \ \textcolor{Red}{\vert} \ \star \ \textcolor{White}{\vert} \ \star\]correspond à \[3 + 2\] \[~\] \[~\] \[~\]
\[ \star \ \textcolor{Red}{\vert} \ \star \! \ \textcolor{White}{\vert} \ \star \! \ \textcolor{Red}{\vert} \ \star \ \textcolor{White}{\vert} \ \star\]correspond à \[1 + 2 + 2\] \[~\] \[~\] \[~\]
\[ \star \ \textcolor{Red}{\vert} \ \star \! \ \textcolor{Red}{\vert} \ \star \! \ \textcolor{Red}{\vert} \ \star \ \textcolor{White}{\vert} \ \star\]correspond à \[1 + 1 + 1 + 2\] \[~\] \[~\] \[~\]
\[ \star \ \textcolor{White}{\vert} \ \star \! \ \textcolor{White}{\vert} \ \star \! \ \textcolor{White}{\vert} \ \star \ \textcolor{White}{\vert} \ \star\] correspond à \[5\] \[~\] \[~\] \[~\]
alors que \[ \star \ \textcolor{Red}{\vert} \ \star \! \ \textcolor{Red}{\vert} \ \star \! \ \textcolor{Red}{\vert} \ \star \ \textcolor{Red}{\vert} \ \star\]correspond à \[1 + 1 + 1 + 1 +1\] \[~\] \[~\] \[~\]
Comme il y a \(n-1\) séparateurs et que chaque séparateur a deux états, activé ou non, il y a \(2^{n-1}\) façons différentes d’activer les séparateurs, et donc autant de façons de faire des piles de \(n\) objets identiques avec ordre ou, de manière équivalente, autant de façons d’exprimer un nombre naturel comme une somme d’entiers strictement positifs dans laquelle l’ordre est important.
Les partitions
Comme on l’a répété quelques fois, dans le calcul des compositions, l’ordre est important. Si, au contraire, on laisse tomber cette contrainte, il s’agit plutôt de partitions. Par exemple, il y a seulement cinq façons d’exprimer 4 comme une somme d’entiers strictement positifs (au lieu de 8 pour les compositions) : \[4, \quad 3 + 1, \quad 2 + 2, \quad 2 + 1 + 1, \quad 1 + 1 + 1 +1 \]Pour 5, c’est sept façons (au lieu de 16 pour les compositions) : \[5, \quad 4 + 1, \quad 3 + 2, \quad 3 + 1 + 1, \quad 2 + 2 + 1, \quad 2 + 1 + 1 + 1, \quad 1 + 1 + 1 + 1 + 1\]Le fait de ne plus considérer l’ordre rend la chose franchement plus difficile à étudier. Il n’y a pas de formule simple pour exprimer le nombre de partitions. Hardy et Ramanujan ont trouvé que si \(p(n)\) est le nombre de partitions de \(n\), alors \[p(n) \approx \frac{1}{4n\sqrt{3}}e^{\pi\sqrt{\frac{2n}{3}}}\]Cette dernière approximation est modifiée plus tard par Hans Rademacher qui obtient la série convergente suivante[1] \[p(n) = \frac{1}{\pi\sqrt{2}}\sum_{k=1}^{\infty}A_{k}(n)\sqrt{k}\cdot \frac{\text{d}}{\text{d}n}\left(\frac{1}{\sqrt{1-\frac{1}{24}}}\cdot \sinh\!\left(\frac{\pi}{k}\sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)}\right)\right)\]dans laquelle \[A_{k}(n) = \sum_{0\leq h<k}e^{\pi i \cdot s(h,k) -\frac{2\pi i n h}{k}}\]avec \[s(h,\, k) = \sum_{r=1}^{k-1}\frac{r}{k}\left(\frac{hr}{k} – \left\lfloor\frac{hr}{k}\right\rfloor – \frac{1}{2}\right)\]On comprend que l’étude en profondeur des partitions va bien au delà de la portée de ce blogue !
[1] Conway , John H. et Richard Guy, The Book of Numbers, Copernicus, 1998