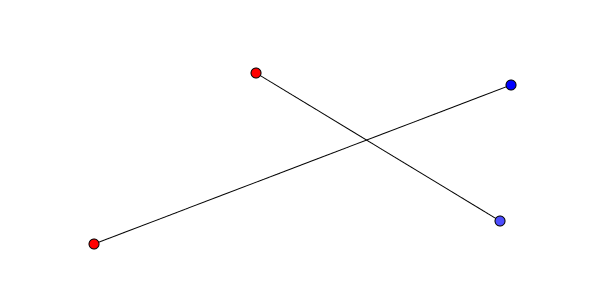
On considère \(n\) points rouges et \(n\) points bleus dispersés dans le plan, trois points quelconques n’étant pas colinéaires. Est-il toujours possible de relier les \(n\) points rouges aux \(n\) points bleus avec des segments de telle sorte qu’aucun segment n’en croise un autre ?
En essayant quelques cas à la main avec un \(n\) petit, on se doute que la réponse sera affirmative mais avec un \(n\) grand, la démarche qui nous mène à une solution n’est pas claire. Comment choisir les points et les relier ? Comment éviter systématiquement les croisements ?
Si deux segments se croisent, il est effectivement possible et même facile de remplacer ces segments par d’autres qui ne partagent aucun point d’intersection.
Considérons le quadrilatère convexe formé par les quatre points aux extrémités des segments qui se croisent et qui possède les deux segments comme diagonales.
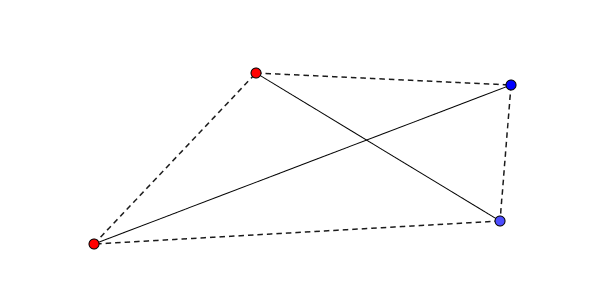
Deux des côtés (opposés) relient évidemment deux points de la même couleur ; cependant les deux autres côtés (opposés aussi) relient un point rouge à un point bleu. On propose donc de remplacer les segments initiaux par ces deux côtés opposés du polygone.
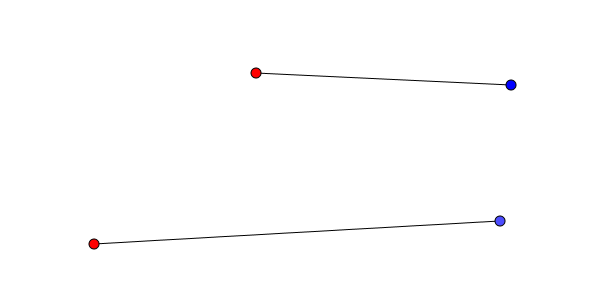
Et hop ! Les segments ont été remplacés par d’autres qui ne se croisent plus.
L’approche à emprunter qui nous permettrait de relier les \(n\) points bleus aux \(n\) points rouges en évitant les croisements étant nébuleuse, on adopte plutôt avec une approche radicalement différente : on relie les points rouges aux points bleus sans faire attention, de manière arbitraire et on essaie de les démêler ensuite. Notons au passage qu’il y a \(n!\) façons de relier les \(n\) points bleus aux \(n\) points rouges. 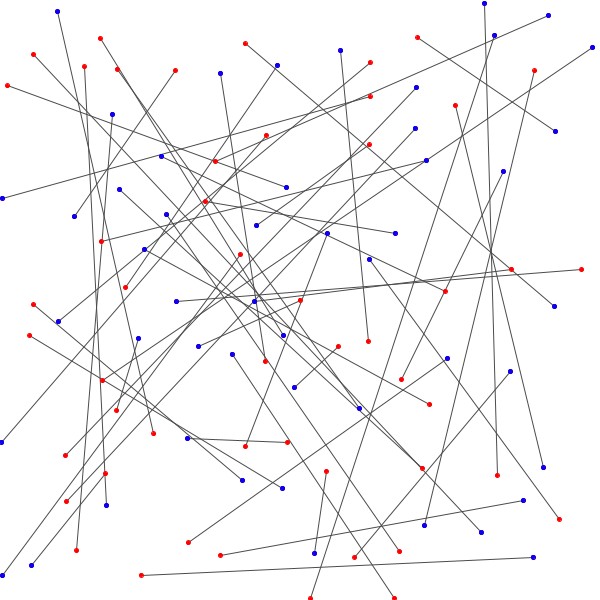
Est-il possible alors de décroiser tous les segments avec la technique décrite ci-haut ?
En effet, il suffit d’identifier des segments qui se croisent puis de les remplacer par d’autres qui ne se croisent pas. Le nombre d’intersections diminue ainsi de \(1\) chaque fois qu’on fait appel à la technique précédente. Si on considère le nombre d’intersections total, en procédant de cette manière, à répétition, à chaque étape le nombre d’intersections diminuant de \(1\), éventuellement, on devrait atteindre le nombre désiré de \(0\) intersection, non ?
Vraiment ?
Hélas, ce n’est malheureusement pas si simple. Il est fort possible que les côtés du quadrilatère choisis croisent à leur tour d’autres segments et que le nombre d’intersections reste le même ou pire, augmente. Oups.
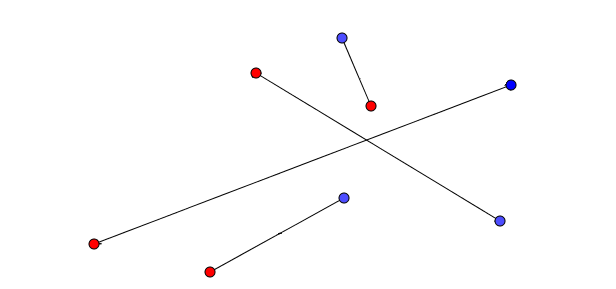
On identifie le quadrilatère.
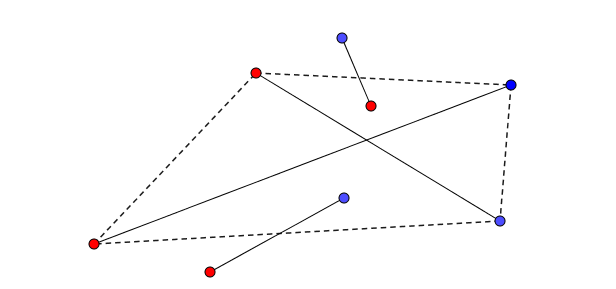
devient
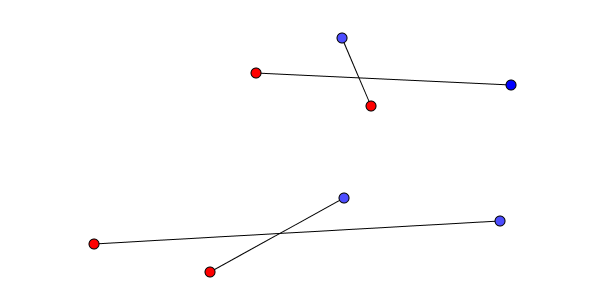
Dans ce cas-ci le nombre d’intersections augmente.
Cependant, tout n’est pas perdu !
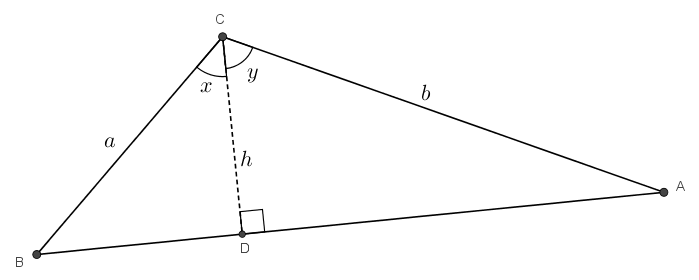
L’idée de remplacer les deux segments qui forment les diagonales par les côtés du quadrilatère est la bonne. Mais ce n’est pas le nombre d’intersections qui doit nous intéresser : c’est plutôt longueur totale des segments. Une observation importante à faire est celle-ci : la somme des mesures des deux segments qui se croisent est supérieure à la somme des mesures des côtés opposés du quadrilatère qui les remplacent.
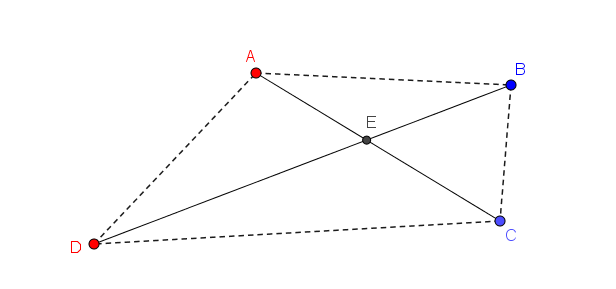
Considérons que les segments \(\textcolor{Red}{A}\textcolor{Blue}{C}\) et \(\textcolor{Blue}{B}\textcolor{Red}{D}\) se croisent en \(E\). Avec l’inégalité du triangle, on sait que \[m\overline{AE} + m\overline{EB} > m\overline{AB}\]et que \[m\overline{DE} + m\overline{EC} > m\overline{DC}\]La somme de ces expressions correspond à \[m\overline{AE} + m\overline{EB} + m\overline{DE} + m\overline{EC} > m\overline{AB} + m\overline{DC}\]ce qui fait \[m\overline{AE} +m\overline{EC}+ m\overline{DE} + m\overline{EB} > m\overline{AB} + m\overline{DC}\]ou plus simplement \[m\overline{AC} + m\overline{DB}> m\overline{AB} + m\overline{DC}\]ce qui est le résultat recherché.
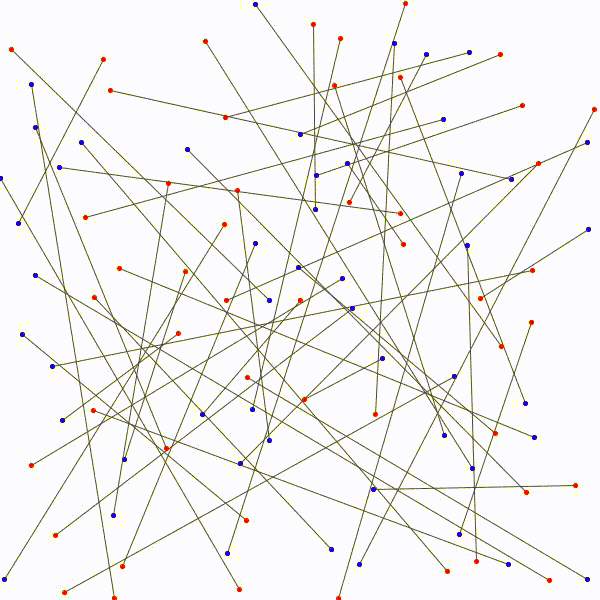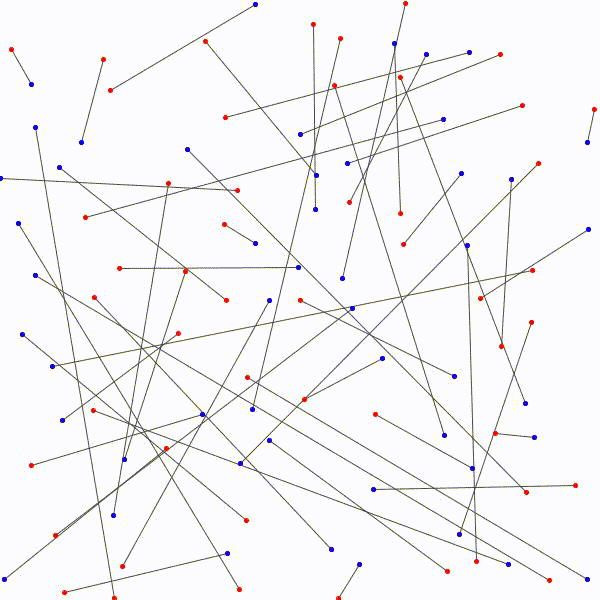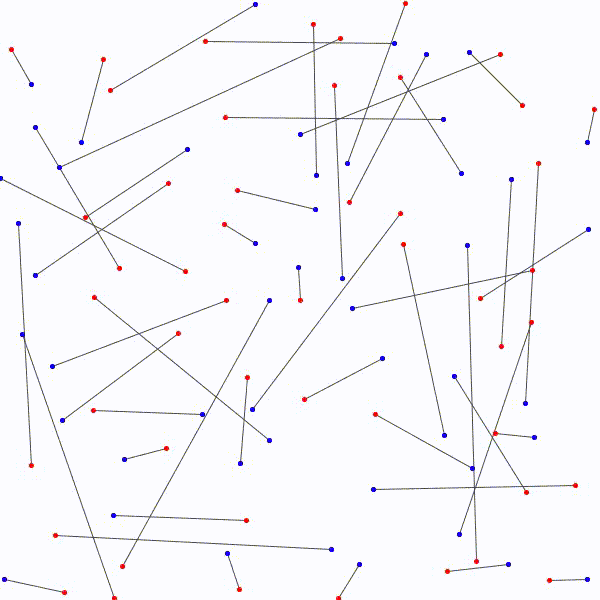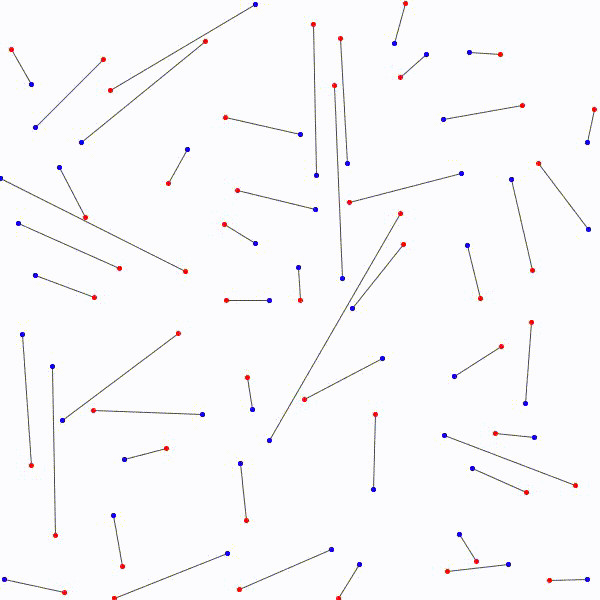
Il y a \(n!\) façons différentes de lier les \(n\) points bleus et les \(n\) points rouges avec \(n\) segments. Considérons la façon de les relier qui minimise la somme des mesures des \(n\) segments. On prétend qu’il n’y a à ce moment aucuns segments qui se croisent. En effet, s’il y a avait un croisement, on pourrait appliquer la procédure décrite ci-dessus et remplacer les segments par les côtés du quadrilatère correspondant pour diminuer la somme des mesures des \(n\) segments. C’est la contradiction recherchée car on avait considéré la façon de relier les segments qui minimisait la longueur totale \(n\) segments et on en a trouvé une autre dans laquelle la longueur totale était encore plus petite !
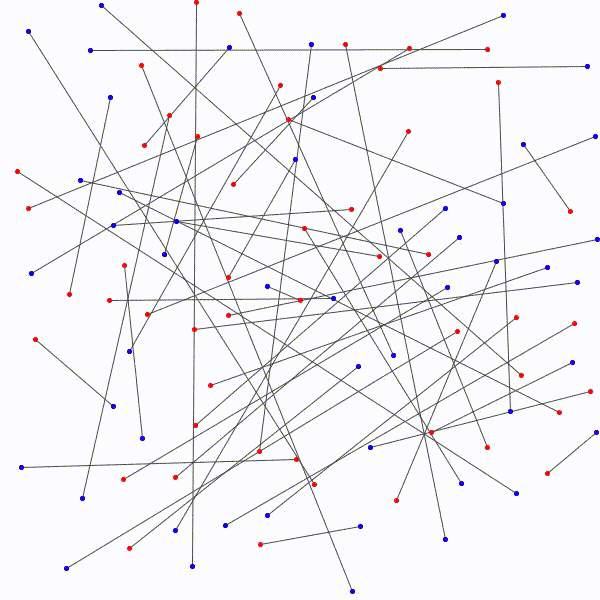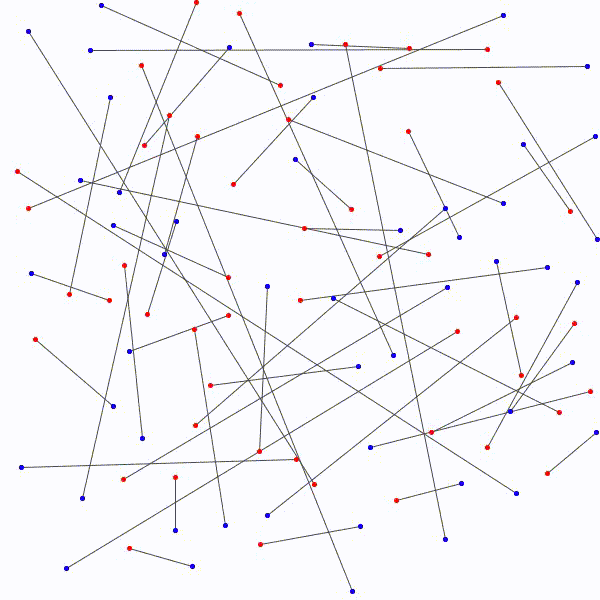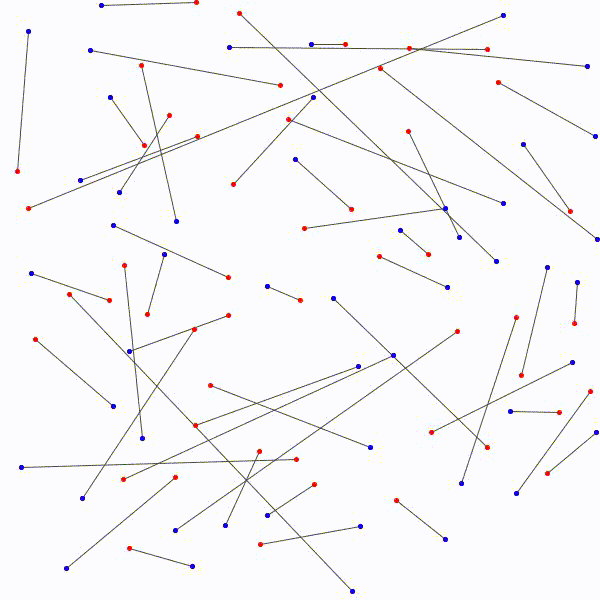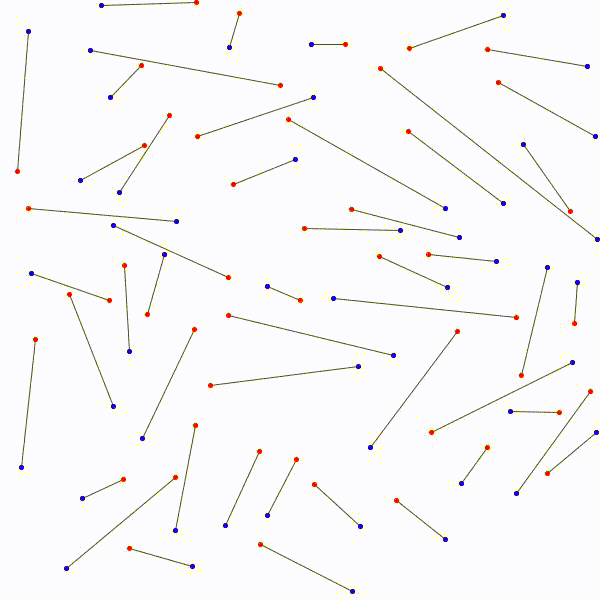
Il est donc toujours possible…
de relier les \(n\) points rouges…
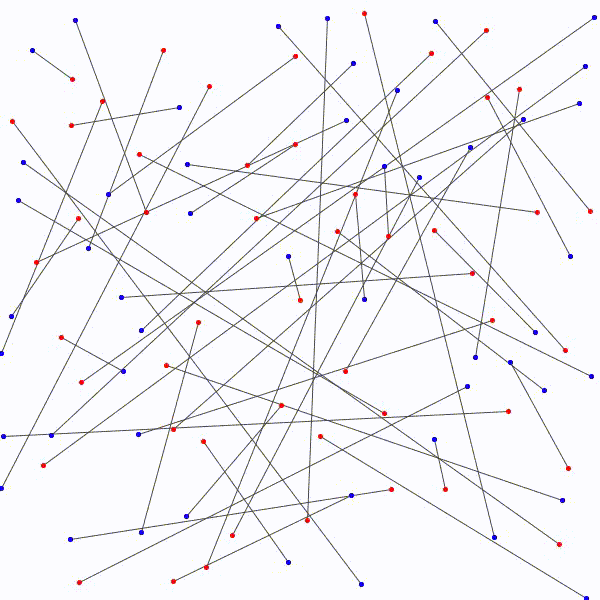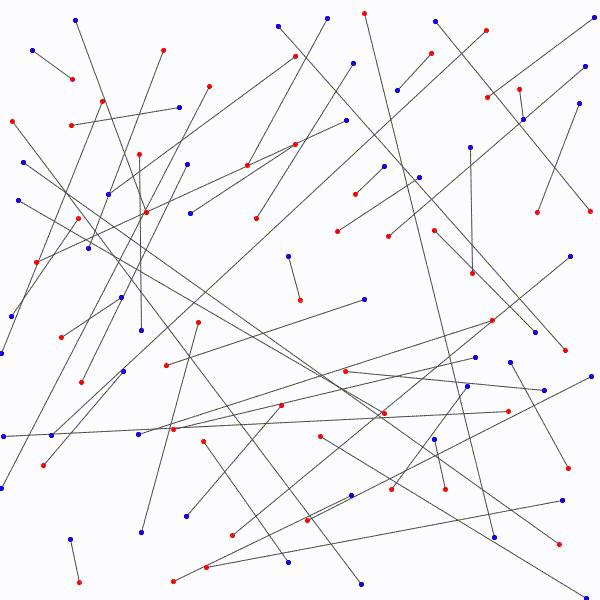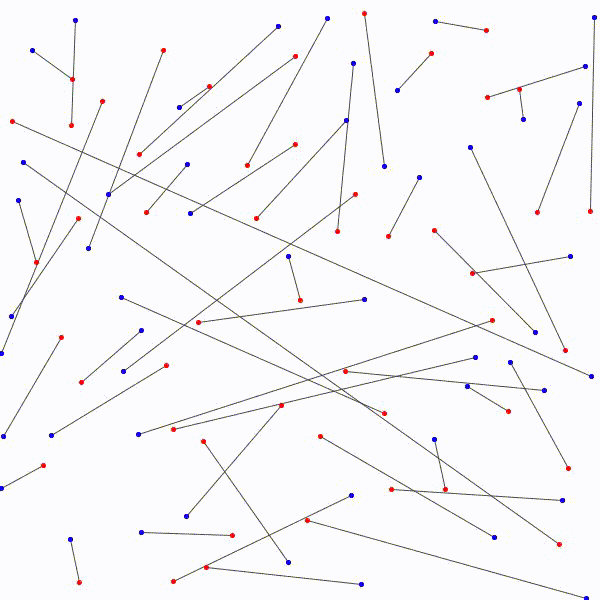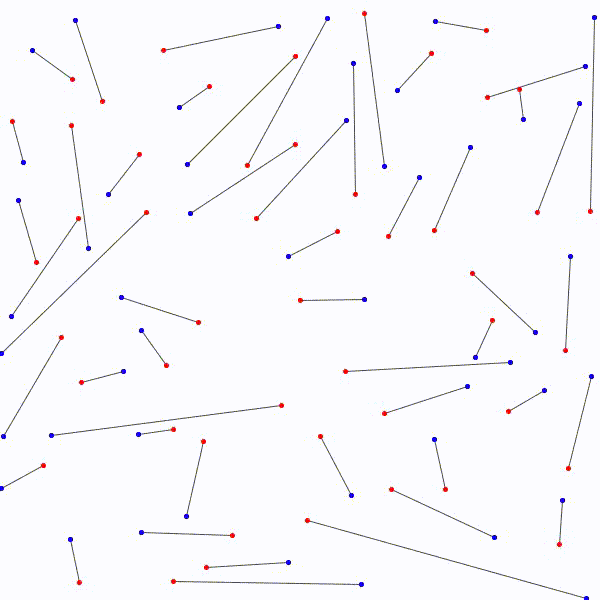
aux \(n\) points bleus…
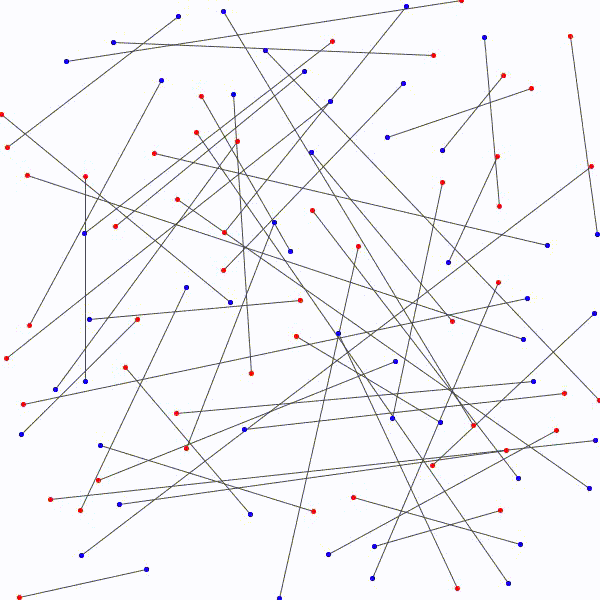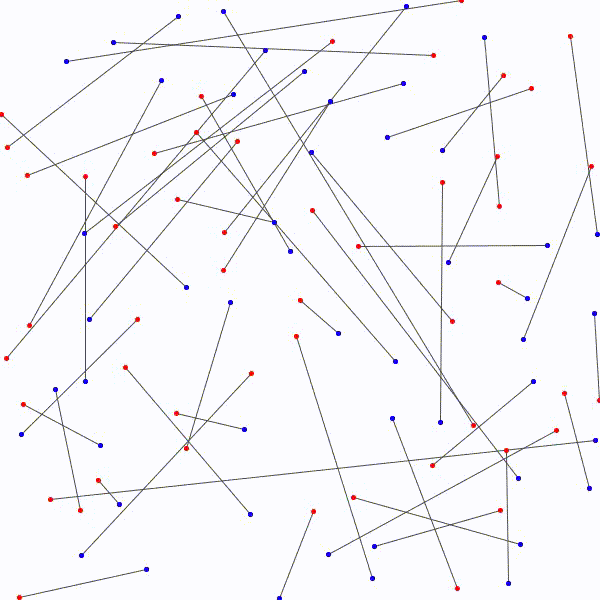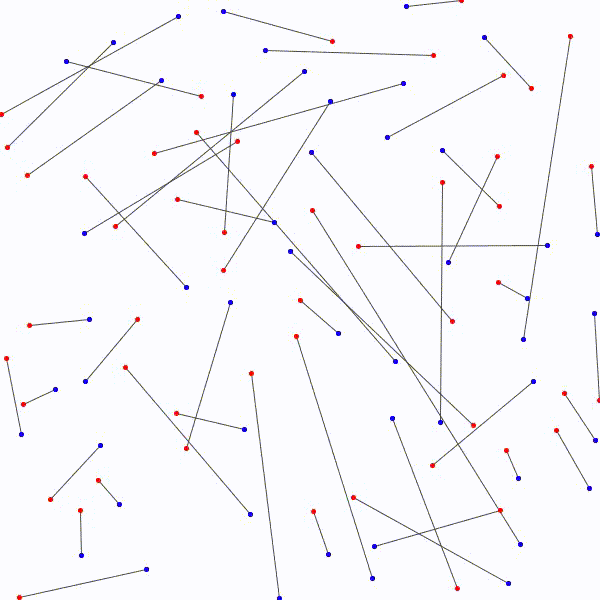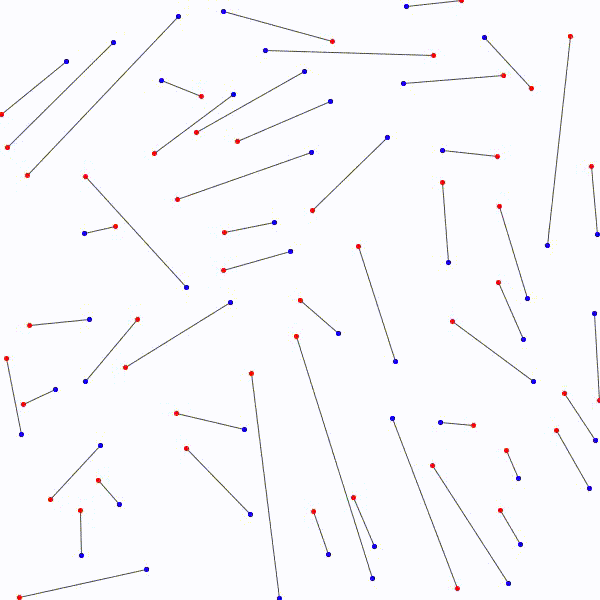
sans que deux segments ne se croisent.
Notons que notre réflexion repose sur le fait qu’il existe (au moins) une façon minimale de relier les points mais elle n’exclut pas qu’il y ait, d’abord, plus qu’une façon minimale (d’ailleurs, est-ce possible ?) et ensuite plusieurs autres façons valides de relier les points (donc sans aucun croisement) mais dans lesquelles la longueur totale des segments n’est pas minimale.