Les enseignants de quatrième secondaire débutent souvent l’année avec le chapitre sur la factorisation. Voici une question sur laquelle je suis tombé en parcourant /r/learnmath :
Factorisez \[x^{4} + 4x^{2} + 16\]
Le polynôme a une allure parfaitement inoffensive, on peut le considérer comme un polynôme du deuxième degré en \(x^{2}\). La réponse attendue : on peut effectuer le changement de variable suivant\[y=x^{2}\]et factoriser le trinôme\[y^{2} + 4y + 16\]Or, le discriminant étant négatif \[\Delta=4^{2}-4(1)(16)<0\]ce dernier polynôme ne se factorise pas ! Oups ! Conclusion (erronée) : le polynôme du départ ne se factorise pas.
Le problème est que, dans les réels, il existe des facteurs « premiers » du premier et du deuxième degré. Ainsi, un polynôme de degré \(4\) peut posséder (distincts ou non) quatre facteurs du premier degré, deux facteurs du premier degré et un du deuxième ou deux facteurs du deuxième degré. C’est bien sûr le troisième cas qui nous intéresse ici et qui cause problème. Il est d’ailleurs facile de vérifier que\[x^{4} + 4x^{2} + 16 = (x^{2}-2x + 4)(x^{2} +2x + 4)\]Un produit de deux trinômes irréductibles ! Comment, alors, arriver à une telle conclusion ? Pour ce cas précis, on peut chercher à retrouver une différence de carrés. Et pour ce faire, on commence par « compléter le carré » en ajoutant un terme en \(x^{2}\). On obtient \[x^{4} \textcolor{Blue}{+ 8x^{2}} + 16\textcolor{Blue}{-8x^{2}} + 4x^{2}\]ce qui fait en factorisant le trinôme carré parfait\[\left(x^{2}+ 4\right)^{2}-\,4x^{2}\]Et voilà ! Le deuxième terme étant lui-même un carré \[\left(x^{2}+4\right)^{2}-\,\left(2x\right)^{2}\]on obtient une expression qui se factorise facilement\[\left(x^{2}-2x+4\right)\left(x^{2}+2x+4\right)\]À ce moment, le lecteur reste peut-être sur sa faim : ça semble trop beau, les coefficients ont dû être choisis exprès ! En partant de \[x^{4} + bx^{2} + c\]on peut vérifier les étapes suivantes \begin{align*}x^{4}+bx^{2}+c &=x^{4}+2\sqrt{c}\,x^{2}+c-2\sqrt{c}\,x^{2}+bx^{2} \\ \\ &=\left(x^{2} + \sqrt{c}\,\right)^{2}-\left(2\sqrt{c}-b\right)\,x^{2} \\ \\ &=\left(x^{2} + \sqrt{c}\,\right)^{2}-\left(\sqrt{2\sqrt{c}-b}\,x\right)^{2} \\ \\ &=\left(x^{2}-\sqrt{2\sqrt{c}-b}\,x+\sqrt{c}\,\right)\left(x^{2}+\sqrt{2\sqrt{c}-b}\,x+\sqrt{c}\,\right) \end{align*}qui mènent, toujours dans ce cas-ci, à la bonne factorisation.
En continuant la démarche de l’enseignant, et en prenant un petit détour par les complexes, il est aussi possible d’arriver à la factorisation demandée. Trouver les racines complexes d’un polynôme du quatrième degré est en général une tâche fort fastidieuse, mais dans le cas de polynôme du type\[x^{4}+4x^{2}+16\]c’est long mais plutôt facile. En changeant la variable\[y = x^{2}\]on obtient\[y^{2}+4y+16\]ce qui nous donne comme racines\[y=\frac{-4\pm\sqrt{-48}}{2}\]c’est-à-dire\begin{align*}y&=\frac{-4 \pm \sqrt{-48}}{2}\\ \\ &=\frac{-4\pm \sqrt{16 \cdot 3 \cdot -1}}{2} \\ \\ &=\frac{-4\pm 4\sqrt{3}\,i}{2} \\ \\ &=-2 \pm 2\sqrt{3}\, i\end{align*}On obtient donc comme racines du polynôme initial \[x = \pm\sqrt{-2\pm 2\sqrt{3}\, i}\]En considérant la première de ces quatre racines\[x_{1}=\sqrt{-2 + 2\sqrt{3}\, i}\]et en posant\[x_{1}=\alpha+\beta i\]on obtient\[\alpha + \beta i = \sqrt{-2 + 2\sqrt{3}\, i}\]En élevant au carré on a \[\alpha^{2}\ – \ \beta^{2} + 2\alpha \beta i = -2 + \sqrt{3}\, i\]duquel on tire un système d’équations \begin{align*}\alpha^{2}-\beta^{2}&=-2 \\ \\ 2\alpha \beta &= 2\sqrt{3}\end{align*}qu’on peut réécrire comme\begin{align*}\alpha^{2}-\beta^{2}&=-2 \\ \\ \alpha^{2}\beta^{2}&=3\end{align*}et qui nous donne\begin{align*}\alpha^{2}&=1 \\ \\ \beta^{3}&=3\end{align*}On peut donc réécrire la première racine comme \[x_{1} = \sqrt{-2+2\sqrt{3}\, i} = 1 + \sqrt{3}\, i\]et de manière analogue, les trois autres racines \begin{align*}x_{2}&=\sqrt{-2-2\sqrt{3}\,i} = 1-\sqrt{3}\,i \\ \\ x_{3}&=-\sqrt{-2+2\sqrt{3}\,i}=-1-\sqrt{3}\,i \\ \\ x_{4}&=-\sqrt{-2-2\sqrt{3}\,i}=-1+\sqrt{3}\,i\end{align*}Ainsi, lorsqu’on factorise (dans les complexes) : \[x^{4}+4x^{2}+16 = (x-x_{1})(x-x_{2})(x-x_{3})(x-x_{4})\]et qu’on remarque que\begin{align*}x_{1}+x_{2}&=\left(1+\sqrt{3}\,i\right) + \left(1-\sqrt{3}\,i\right) =2 \\ \\ x_{1}x_{2}&= \left(1+\sqrt{3}\,i\right)\left(1-\sqrt{3}\,i\right) = 4 \\ \\ x_{3}+x_{4}&=\left(-1-\sqrt{3}\,i\right)+\left(-1+\sqrt{3}\,i\right)=-2 \\ \\ x_{3}x_{4} &= \left(-1-\sqrt{3}\,i\right)\left(-1+\sqrt{3}\,i\right) = 4\end{align*}on obtient, en réunissant les facteurs du premier degré deux à deux,\[(x-x_{1})(x-x_{2})(x-x_{3})(x-x_{4}) = \left(x^{2}-\left(x_{1}+x_{2}\right)x + x_{1}x_{2}\right)\left(x^{2}-\left(x_{3}+x_{4}\right)x+x_{3}x_{4}\right)\]c’est-à-dire le résultat recherché\[x^{4} + 4x^{2}+16 = \left(x^{2}-2x+4\right)\left(x^{2}+2x+4\right)\]

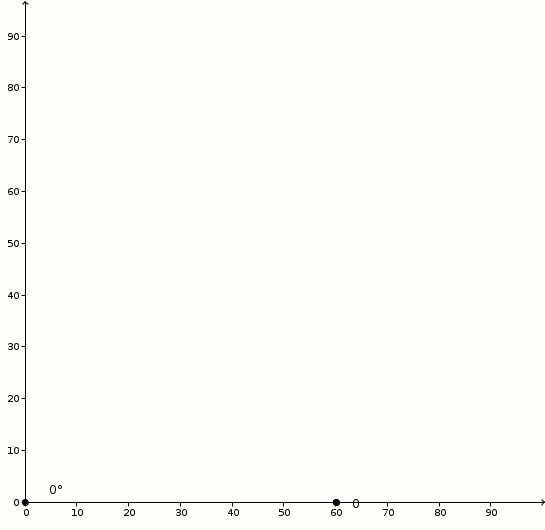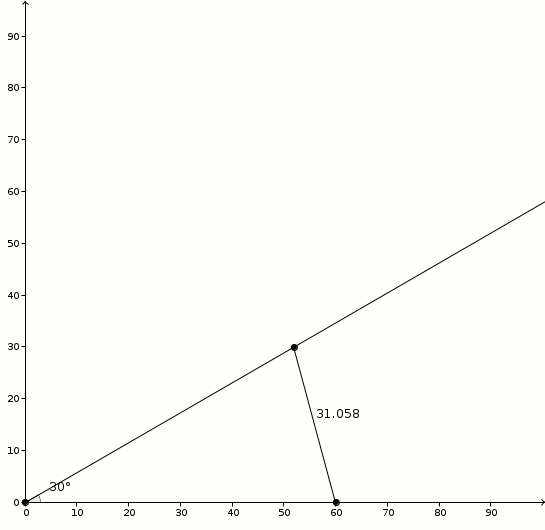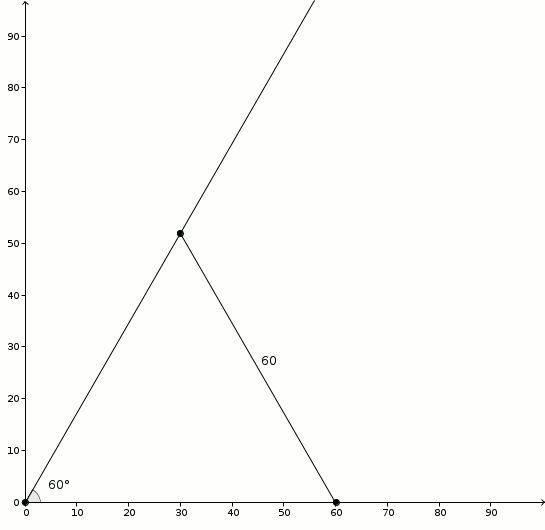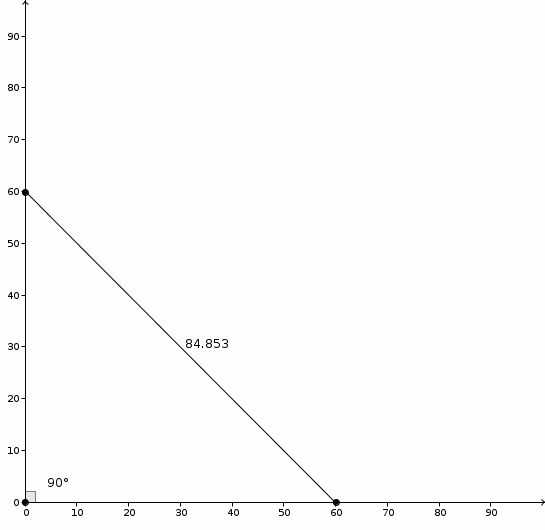 Pourquoi est-ce que ça fonctionne ? On considère un angle \(\alpha\) et on procède tel qu’indiqué. En marquant les côtés de l’angle à la même distance (ici, \(60\) millimètres), on dessine un triangle isocèle. Et comme c’est un triangle isocèle, la bissectrice de l’angle \(\alpha\) sera aussi une médiatrice.
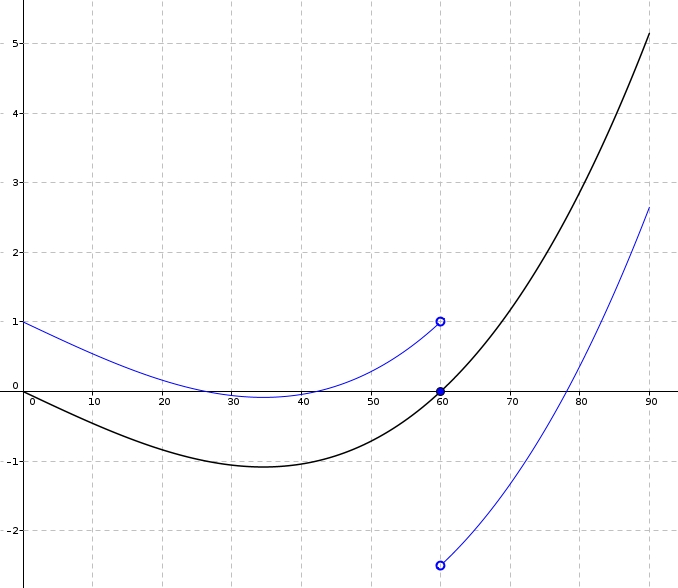
Pourquoi est-ce que ça fonctionne ? On considère un angle \(\alpha\) et on procède tel qu’indiqué. En marquant les côtés de l’angle à la même distance (ici, \(60\) millimètres), on dessine un triangle isocèle. Et comme c’est un triangle isocèle, la bissectrice de l’angle \(\alpha\) sera aussi une médiatrice.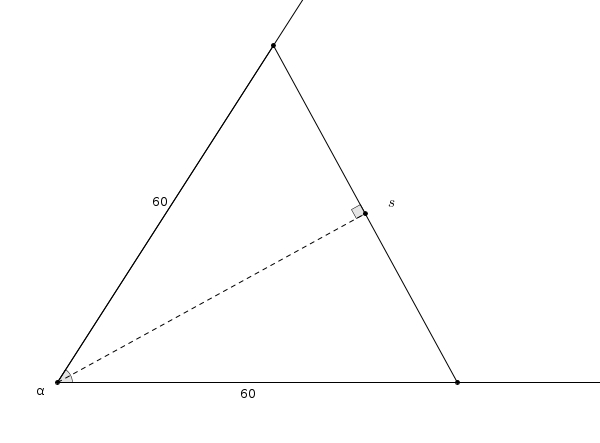 Ainsi, en n’oubliant pas que \[1^{\circ} = \frac{\pi}{180}\]on observe la relation suivante dans les triangles rectangles formés par la bissectrice/médiatrice \[\sin\left(\frac{\pi}{180}\cdot \frac{\alpha}{2}\right) = \frac{\frac{s}{2}}{60}\]et dans laquelle \(\alpha\) est exprimé en degrés. De \[\sin\left(\frac{\pi}{360}\alpha\right) = \frac{s}{120}\]on utilise maintenant deux approximations si grossières qu’elles vous feront perdre, peut-être, tout espoir d’obtenir une expression utile au final. Et pourtant ! D’abord, pour de petits angles (exprimés en radian), on a \[\sin\left(\theta\right) \approx \theta\]ce qui donne comme première approximation \[\frac{\pi}{360} \approx \frac{s}{120}\]et en utilisant (ma parole !) \[\pi \approx 3\]on obtient ensuite \[\frac{3}{360} \alpha \approx \frac{s}{120}\]C’est donc avec un certain scepticisme qu’on retrouve effectivement \[\alpha \approx s\]Est-ce que l’approximation est fiable ? Le graphique suivant montre la relation entre \(\alpha\) (abscisses) et \(\alpha-s\) (ordonnées).
Ainsi, en n’oubliant pas que \[1^{\circ} = \frac{\pi}{180}\]on observe la relation suivante dans les triangles rectangles formés par la bissectrice/médiatrice \[\sin\left(\frac{\pi}{180}\cdot \frac{\alpha}{2}\right) = \frac{\frac{s}{2}}{60}\]et dans laquelle \(\alpha\) est exprimé en degrés. De \[\sin\left(\frac{\pi}{360}\alpha\right) = \frac{s}{120}\]on utilise maintenant deux approximations si grossières qu’elles vous feront perdre, peut-être, tout espoir d’obtenir une expression utile au final. Et pourtant ! D’abord, pour de petits angles (exprimés en radian), on a \[\sin\left(\theta\right) \approx \theta\]ce qui donne comme première approximation \[\frac{\pi}{360} \approx \frac{s}{120}\]et en utilisant (ma parole !) \[\pi \approx 3\]on obtient ensuite \[\frac{3}{360} \alpha \approx \frac{s}{120}\]C’est donc avec un certain scepticisme qu’on retrouve effectivement \[\alpha \approx s\]Est-ce que l’approximation est fiable ? Le graphique suivant montre la relation entre \(\alpha\) (abscisses) et \(\alpha-s\) (ordonnées).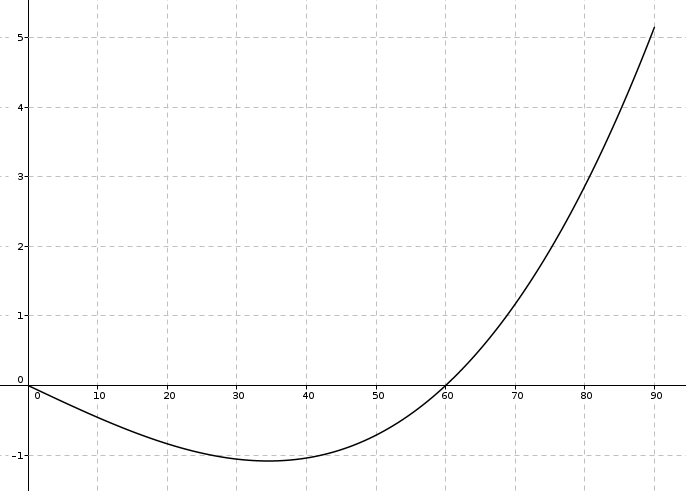 On remarque que pour des angles entre \(0^{\circ}\) et (environ) \(75^{\circ}\), l’erreur est de moins de \(2^{\circ}\). Pas mal ! Après \(75^{\circ}\), ça se gâte un peu, et l’erreur culmine avec un maximum d’environ \(5^{\circ}\) lorsque l’angle est près d’un angle droit. Cependant, toutes proportions gardées, l’erreur de \(5^{\circ}\) reste quand même relativement petite pour cette approximation très économique.
On remarque que pour des angles entre \(0^{\circ}\) et (environ) \(75^{\circ}\), l’erreur est de moins de \(2^{\circ}\). Pas mal ! Après \(75^{\circ}\), ça se gâte un peu, et l’erreur culmine avec un maximum d’environ \(5^{\circ}\) lorsque l’angle est près d’un angle droit. Cependant, toutes proportions gardées, l’erreur de \(5^{\circ}\) reste quand même relativement petite pour cette approximation très économique.