La dénombrabilité de \(\mathbb{N}\times \mathbb{N}\) fait souvent l’objet de jolies preuves, comme celle-ci, une « preuve sans mot »,
En voici une autre plus explicite. On considère la fonction \(g : \mathbb{N} \times \mathbb{N}\to \mathbb{N}\) telle que \[g(x, y)\ =\ 2^x\, \cdot \, 3^y\]
On note que \(g\) n’est pas surjective, parce qu’il existe des nombres \(n\in \mathbb{N}\) dont la décomposition en facteurs premiers incluent des facteurs autres que \(2\) ou \(3\). Mais la fonction \(g\) est néanmoins injective car le Théorème fondamental de l’arithmétique (coucou Euclide !) nous assure que chaque couple \((x, \, y)\) est associé par la fonction \(g\) à un unique nombre naturel \(2^x\, \cdot\, 3^y\). C’est suffisant pour montrer la dénombrabilité de \(\mathbb{N} \times \mathbb{N}\) puisque \(\mathbb{N} \times \mathbb{N}\) est en bijection avec un sous-ensemble de \(\mathbb{N}\). Et comme un sous-ensemble d’un ensemble dénombrable est lui même dénombrable, \(\mathbb{N} \times \mathbb{N}\) est dénombrable.
Références : Wikipedia : The Cantor pairing function assigns one natural number to each pair of natural numbers, image par Cronholm144
Croom, Fred H., Principles of Topology, 2016
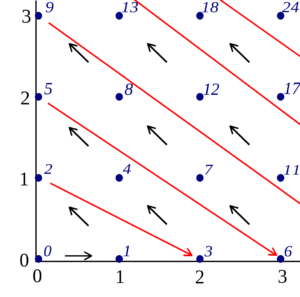
Les trois flèches, en se repliant, forment un ruban de Möbius (un ruban avec un demi-tour), un objet mathématique fascinant ! Le pictogramme soumis par Anderson, à l’époque, tenait le triangle formé par les trois flèches en équilibre sur un de ses sommets. Aujourd’hui, le triangle repose plus souvent sur sa base (rotation de 60° par rapport à l’original), tel que dans le pictogramme ci-dessus.
