Lewis Carrol was the pen name for mathematician C. L. Dodgson. He wrote mathematics books under his own name, but invented his pseudonym by translating his first two names, Charles Lutwidge, into Latin, producing Carolus Lodovicus, which he then Anglicised and reversed in order.
Siobhan Roberts (2006), King of Infinite Space : Donald Coxeter, the Man Who Saved Geometry
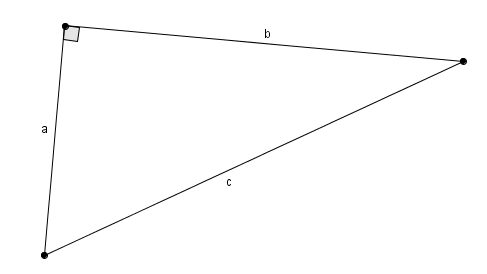
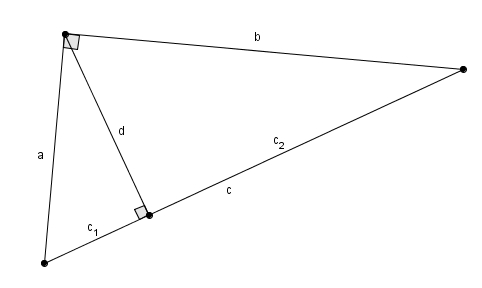
Grâce notamment aux logiciels de géométrie dynamique, il est tout à fait remarquable de faire découvrir aux élèves que dans n’importe quel triangle, le plus grand côté est toujours opposé au plus grand angle et le plus petit côté au plus petit angle.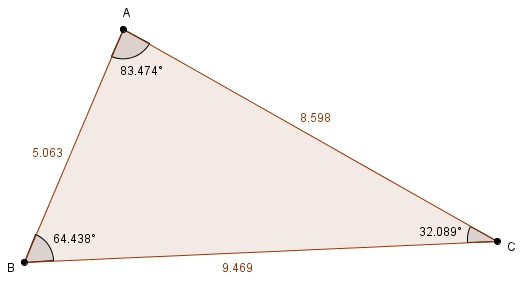
Il est intéressant, à ce moment, de se demander si les côtés opposés et leurs angles respectifs sont dans le même rapport : en d’autres mots, est-ce qu’on \[\frac{a}{\angle A} \overset{?}{=} \frac{b}{\angle B} \overset{?}{=} \frac{c}{\angle C}\]La réponse est bien entendue négative. En réalité, les côtés opposés sont proportionnels non pas aux angles mais aux sinus des angles. C’est la loi des sinus \[\frac{a}{\sin\left(\angle A\right)} = \frac{b}{\sin\left(\angle B\right)} = \frac{c}{\sin\left(\angle C\right)}\]La question est :
Que représente ce rapport entre les côtés opposés et les sinus des angles ?
Avant d’y répondre, et à des fins de complétude pour ce blogue, voici la preuve « cassique » de la loi des sinus telle que vue généralement en quatrième secondaire. Dans un triangle \(ABC\), on trace la hauteur \(CD\) que l’on nomme \(h\).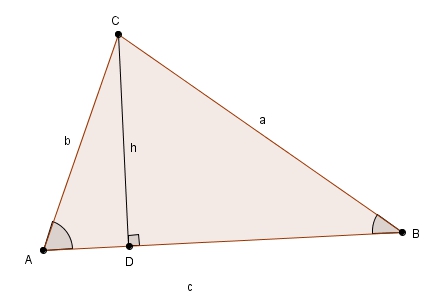
On a d’une part, dans le triangle \(ACD\),\[\sin\left(\angle A\right) = \frac{h}{b} \quad \Rightarrow \quad h = b\sin\left(\angle A\right)\]et, d’autre part, dans le triangle \(BCD\), \[\sin\left(\angle B\right) = \frac{h}{a} \quad \Rightarrow \quad h = a\sin\left(\angle B\right)\]En comparant les expressions obtenues pour la hauteur, on a \[a \sin\left(\angle B\right) = b\sin\left(\angle A\right)\]ou de manière équivalente \[\frac{a}{\sin\left(\angle A\right)} = \frac{b}{\sin\left(\angle B\right)}\]et la preuve est essentiellement complète puisqu’il est possible de répéter la manœuvre avec la hauteur relative au côté \(c\) et par transitivité, on obtient le résultat attendu. La démarche est la même si l’angle est obtus
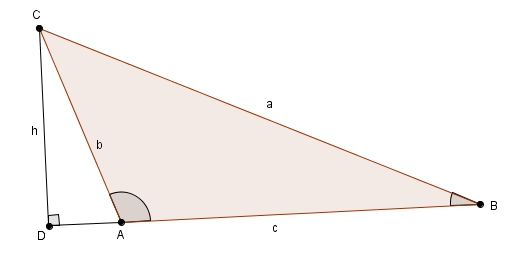puisque dans ce cas, les angles \(CAD\) et \(CAB\) sont supplémentaires et les sinus d’angles supplémentaires sont égaux \[\sin\left(\angle CAD\right) = \sin\left(180^{\circ}-\angle CAD\right)\]Ainsi on a \[\sin\left(\angle CAD\right) = \sin\left(\angle CAB\right)\]
Maintenant, pour répondre à la question, on considère un triangle \(ABC\) et son cercle circonscrit de centre \(O\). On trace le diamètre \(CD\).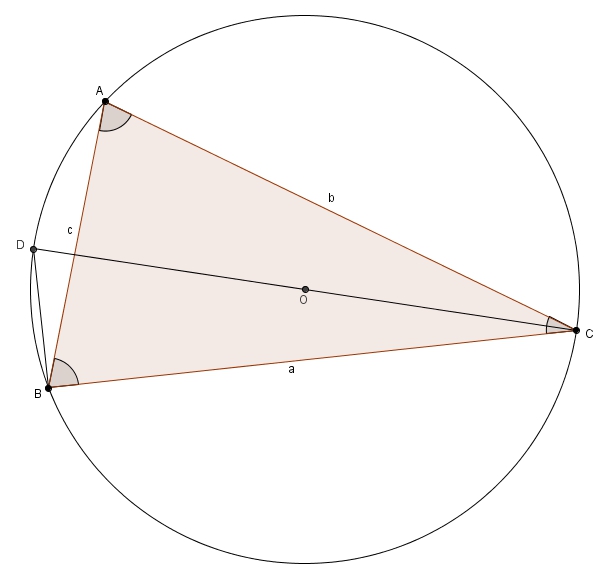
On pose le rayon égal à \(r\). En d’autres mots, m\[m\overline{CD} =2r\]L’angle \(CBD\) est droit puisque le triangle \(CBD\) est inscrit dans un cercle et l’un de ses côtés est un diamètre. On a donc \[\sin\left(\angle D\right) = \frac{a}{m\overline{CD}} = \frac{a}{2r}\]Or, les angles \(D\) et \(A\) sont isométriques puisqu’ils interceptent le même arc. En substituant, on obtient \[\sin\left(\angle A\right) = \frac{a}{2r}\]ou de manière équivalente \[2r = \frac{a}{\sin\left(\angle A\right)}\]En procédant de façon analogue, en considérant les autres angles, on obtient (le cercle circonscrit au triangle étant unique) \[2r = \frac{b}{\sin\left(\angle B\right)}\]et \[2r = \frac{c}{\sin\left(\angle C\right)}\]et donc \[2r = \frac{a}{\sin\left(\angle A\right)} = \frac{b}{\sin\left(\angle B\right)} = \frac{c}{\sin\left(\angle C\right)}\]ce qui complète la preuve. On sait maintenant que le rapport constant entre les côtés opposés et les sinus des angles dans la loi des sinus est égal au diamètre du cercle circonscrit ! Et encore une fois, si le triangle est obtusangle, comme dans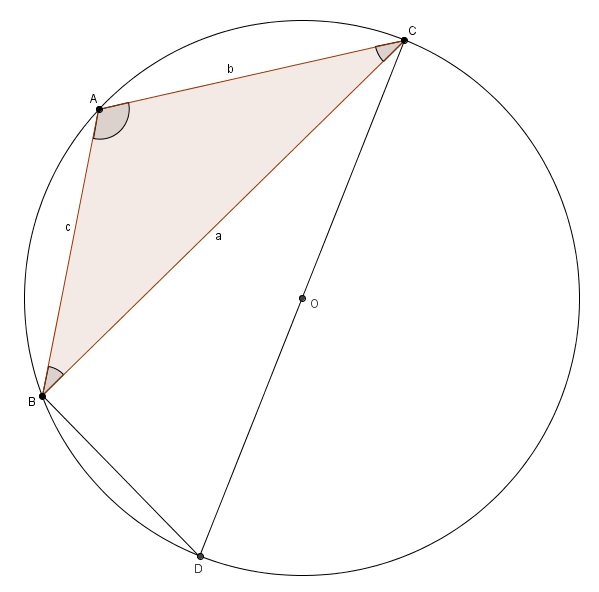
alors pas de problème ! Les angles \(A\) et \(D\) sont supplémentaires puisqu’ils sont des angles opposés dans un quadrilatère inscrit dans un cercle (Proposition III.22 des Éléments d’Euclide). Et comme les sinus d’angles supplémentaires sont égaux, on a bien \[\sin\left(\angle D\right) = \sin\left(\angle A\right)\]
La relation de Pythagore nous dit que dans un triangle rectangle
on a \[a^{2}+ b^{2} = c^{2}\]Les résultats du dernier billet, celui sur l’équation de Fermat, nous permet donc de trouver les dimensions de triangles rectangles dont les trois côtés sont des nombres entiers. Il est possible d’établir un autre lien fort intéressant de la même nature.
En traçant la hauteur issue de l’angle droit (ou relative à l’hypoténuse), le segment \(d\) sur la figure, on crée des triangles semblables. En considérant le grand triangle rectangle initial et un des deux plus petits triangles rectangles semblables, il nous est possible d’établir cette proportion \[\frac{c}{d} = \frac{b}{d}\]ou de manière équivalente \[c = \frac{ab}{d}\]En élevant au carré on obtient \[c^{2} = \frac{a^{2}b^{2}}{d^{2}}\]ce qui nous permet de remplacer dans l’équation initiale\[a^{2} + b^{2} = \frac{a^{2}b^{2}}{d^{2}}\]En divisant par \(a^{2}b^{2}\) on obtient \[\frac{a^{2}}{a^{2}b^{2}} + \frac{b^{2}}{a^{2}b^{2}}=\frac{1}{d^{2}}\]ce qui fait après simplifications \[\frac{1}{a^{2}} + \frac{1}{b^{2}} = \frac{1}{d^{2}}\]C’est l’équation du dernier billet lorsque l’exposant vaut \(-2\). On pose donc \[a = 2pq\left(p^{2}+q^{2}\right), \quad b=\left(p^{2}+q^{2}\right)\left(p^{2}-q^{2}\right), \quad d = 2pq\left(p^{2}-q^{2}\right)\]avec \(p\) et \(q\) deux entiers premiers entre eux et de parité différente, et \(p>q\). Comme\[c = \frac{ab}{d}\]on a bien \[c=\frac{2pq\left(p^{2}+q^{2}\right) \cdot \left(p^{2}+q^{2}\right)\left(p^{2}-q^{2}\right)}{2pq\left(p^{2}-q^{2}\right)} = \left(p^{2}+q^{2}\right)^{2}\]et \(c\) est un entier ! On peut même trouver que la mesure des segments sur l’hypoténuse déterminés par la hauteur (\(c_1\) et \(c_2\) sur la figure) sont elles aussi entières. Par Pythagore, on a \begin{align*}\left(c_{1}\right)^{2}+d^{2} &= a^{2} \\ \\ \left(c_{1}\right)^{2} + \left(2pq\left(p^{2}-q^{2}\right)\right)^{2} &=\left(2pq\left(p^{2}+q^{2}\right)\right)^{2} \\ \\ \left(c_{1}\right)^{2} &= \left(2pq\left(p^{2}+q^{2}\right)\right)^{2}-\left(2pq\left(p^{2}-q^{2}\right)\right)^{2}\end{align*}et en effectuant une mise en évidence simple puis en factorisant la différence de carrés, on trouve\begin{align*}\left(c_{1}\right)^{2} &=\left(2pq\left(p^{2}+q^{2}\right)\right)^{2}-\left(2pq\left(p^{2}-q^{2}\right)\right)^{2} \\ \\ &=4p^{2}q^{2}\left(\left(p^{2}+q^{2}\right)^{2}-\left(p^{2}-q^{2}\right)^{2}\right) \\ \\ &= 4p^{2}q^{2}\left(p^{2}+q^{2}+\left(p^{2}-q^{2}\right)\right)\left(p^{2}+q^{2}-\left(p^{2}-q^{2}\right)\right) \\ \\ &= 4p^{2}q^{2}\left(2p^{2}\right)\left(2q^{2}\right) \\ \\ &= \left(4p^{2}q^{2}\right)^{2}\end{align*}c’est-à-dire\[c_{1}=4p^{2}q^{2}\]un nombre entier ! Puis la même chose avec \begin{align*}\left(c_{2}\right)^{2} + d^{2} &=b^{2} \\ \\ \left(c_{2}\right)^{2} + \left(2pq\left(p^{2}-q^{2}\right)\right)^{2}&=\left(\left(p^{2}+q^{2}\right)\left(p^{2}-q^{2}\right)\right)^{2} \\ \\ \left(c_{2}\right)^{2}&=\left(\left(p^{2}+q^{2}\right)\left(p^{2}-q^{2}\right)\right)^{2}-\left(2pq\left(p^{2}-q^{2}\right)\right)^{2}\end{align*}et encore une fois après une mise en évidence simple et une factorisation d’une différence de carrés, on a \begin{align*}\left(c_{2}\right)^{2}&=\left(\left(p^{2}+q^{2}\right)\left(p^{2}-q^{2}\right)\right)^{2}-\left(2pq\left(p^{2}-q^{2}\right)\right)^{2} \\ \\ &=\left(p^{2}-q^{2}\right)^{2}\left(\left(p^{2}+q^{2}\right)^{2}-\left(2pq\right)^{2}\right) \\ \\ &=\left(p^{2}-q^{2}\right)^{2}\left(p^{2}+q^{2}+2pq\right)\left(p^{2}+q^{2}-2pq\right) \\ \\ &=\left(p^{2}-q^{2}\right)^{2}\left(p+q\right)^{2}\left(p-q\right)^{2}\end{align*}c’est-à-dire \begin{align*}c_{2}&=\left(p^{2}-q^{2}\right)\left(p+q\right)\left(p-q\right) \\ \\ &=\left(p^{2}-q^{2}\right)\left(p^{2}-q^{2}\right)\end{align*}encore un nombre entier ! Pourquoi arrêter le plaisir ? On peut même vérifier que \begin{align*}c_{1}+c_{2} &= 4p^{2}q^{2}+\left(p^{2}-q^{2}\right)^{2} \\ \\ &=4p^{2}q^{2}+p^{4}-2p^{2}q^{2}+q^{4} \\ \\ &=p^{4}+2p^{2}q^{2}+q^{4} \\ \\ &= \left(p^{2}+q^{2}\right)^{2} \\ \\ &=c\end{align*}Tout fonctionne ! C’est un truc pratique pour tout enseignant voulant que les solutions à son exercice sur les relations métriques dans le triangle rectangle soient « arrangées avec le gars des vues ».
