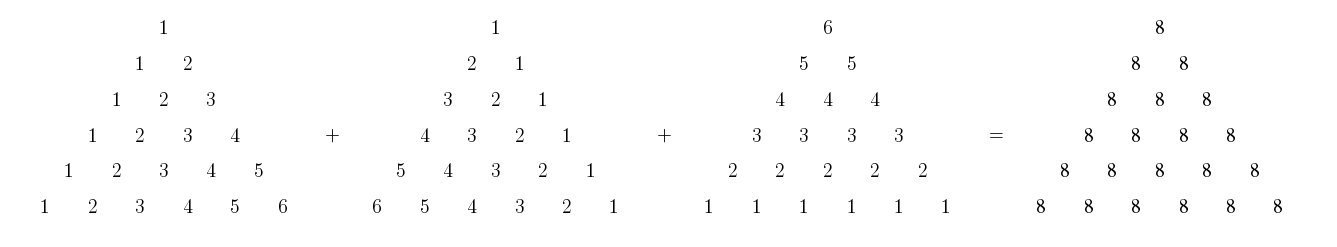
On a vu dans ce billet que le \(n^{\text{e}}\) nombre triangulaire \(t_{n}\) correspond à la somme des \(n\) premiers entiers. \[t_{n}= \frac{n(n+1)}{2}\]

Les premiers nombres triangulaires
Qu’obtient-on si on renchérit et qu’on s’intéresse à la somme des \(n\) premiers nombres triangulaires \[ t_{1}+t_{2} + t_{3} \, + \, \dots \, + \, t_{n} = 1 + 3 + 6\, + \, \dots \, +\, \frac{n(n+1)}{2}\] Géométriquement, on obtient un nombre tétraédrique (ou nombre pyramidal triangulaire). On note le \(n^{\text{e}}\) nombre tétraédrique \(P^{(3)}_{n}\).
Les nombres tétraédriques
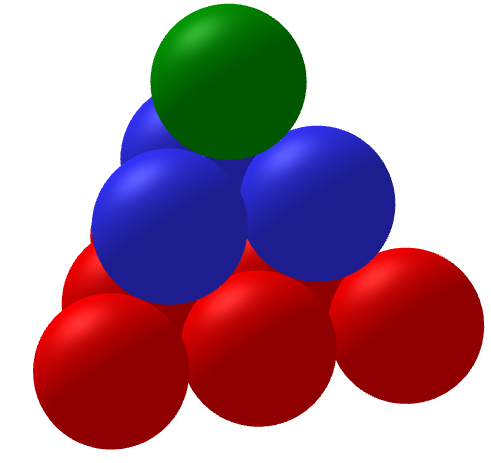
Le troisième nombre tétraédrique, \(P^{(3)}_{3} = 10\)
La table de valeurs suivante présente les premiers nombres tétraédriques.
| \[n\] | \[P^{(3)}_{n}\] |
|---|---|
| \[1\] | \[1\] |
| \[2\] | \[4\] |
| \[3\] | \[10\] |
| \[4\] | \[20\] |
| \[5\] | \[35\] |
| \[6\] | \[56\] |
| \[7\] | \[84\] |
| \[8\] | \[120\] |
| \[9\] | \[165\] |
| \[10\] | \[220\] |
| \[\dots\] | \[\dots\] |
Dans l’image ci-dessous, on le fait pour \(n = 6\).
Considérons un des termes de l’égalité. On appelle \(a_{(i,j)}\) le \(j^{\text{e}}\) nombre (en partant de la gauche) du \(i^{\text{e}}\) étage (en partant du haut) d’un des termes.
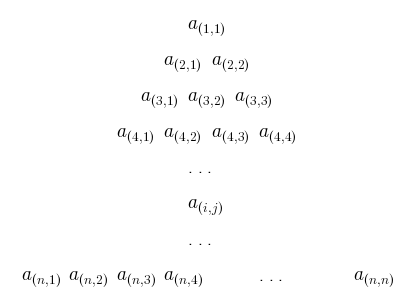
Dans le premier triangle du membre de gauche, \(a_{(i,j)}\) est simplement \(j\). Dans le deuxième triangle, c’est \(i+1-j\), et dans le troisième triangle, c’est \(n+1-i\).
Puisque\[j + i + 1-j + n+1-i = n+2\]en additionnant les nombres \(a_{(i,j)}\) des trois triangles terme à terme, on obtient le \(n^{\text{e}}\) nombre triangulaire de fois le nombre \(n+2\) (le membre de droite de l’égalité). Dans l’exemple, \(n + 2 = 6+2 = 8\). Ainsi, \begin{align*}3\cdot P^{(3)}_{n} &= 3\left(t_{1}+t_{2} + t_{3}+ \, \dots \, + t_{n}\right) \\ \\ &=t_{n} \cdot (n+2) \\ \\ &= \frac{n(n+1)}{2} \cdot (n+2)\end{align*}En divisant par \(3\), on obtient l’expression recherchée \[P^{(3)}_{n} = \frac{n(n+1)(n+2)}{6}\]
[1] The Book of Numbers, Conway, John H. and Richard Guy, 1996, Copernicus New York.