Le titre de ce billet est-il trompeur ? Car on ne commence ni avec une sphère, ni avec du grec, mais plutôt avec un cylindre. La surface courbe (latérale) d’un cylindre est une surface développable : on peut la découper et l’étendre à plat sur un plan. On obtient un rectangle.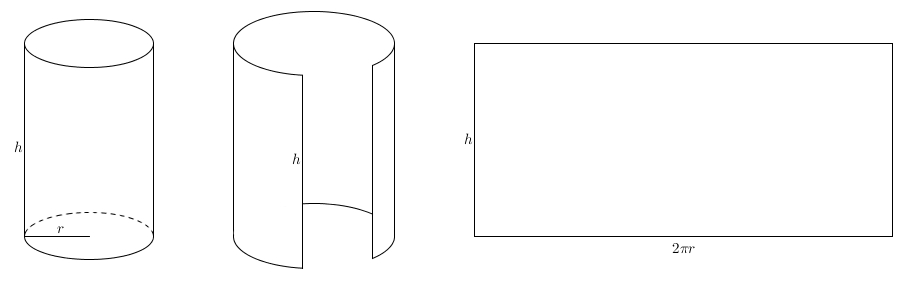 La hauteur du rectangle correspond à la hauteur du cylindre et sa base, à la circonférence du cercle. Ainsi, un cylindre de hauteur \(h\) et dont le rayon de la base est \(r\) aura une aire latérale de \(2\pi rh\). On considère aussi un cône de rayon \(r\) et d’apothème \(a\)
La hauteur du rectangle correspond à la hauteur du cylindre et sa base, à la circonférence du cercle. Ainsi, un cylindre de hauteur \(h\) et dont le rayon de la base est \(r\) aura une aire latérale de \(2\pi rh\). On considère aussi un cône de rayon \(r\) et d’apothème \(a\)
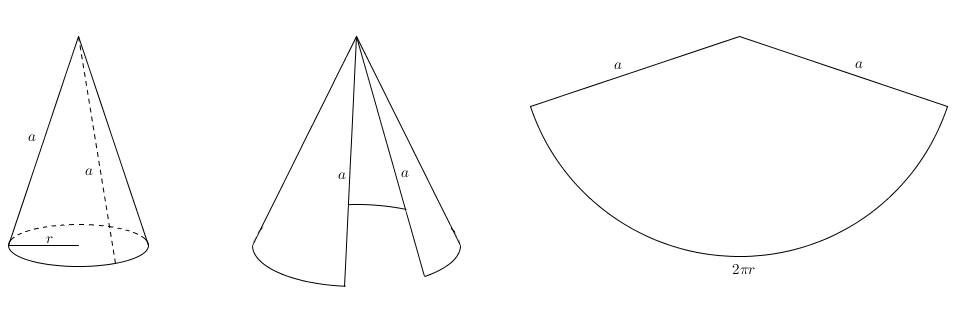
On peut aussi découper le cône et le mettre à plat : on obtient un secteur de disque. On remarque que l’apothème du cône devient le rayon du grand disque et la circonférence de la base du cône devient l’arc de cercle du secteur. L’aire de ce secteur est proportionnel à la mesure de l’arc. Comme l’aire totale du disque complet est \(\pi a^{2}\), la circonférence est \(2\pi a\) et la mesure de l’arc est \(2\pi r\), on obtient\[\frac{\text{Aire du secteur}}{\pi a^{2}}=\frac{2\pi r}{2\pi a}\]ce qui fait après une simplification à droite \[\frac{\text{Aire du secteur}}{\pi a^{2}} = \frac{r}{a}\]puis en multipliant chaque côté par \(\pi a^{2}\) \[\text{Aire du secteur} = \pi a r\]Mais comme ce secteur correspond exactement à la surface latérale du cône, on a en réalité trouvé quelque chose d’assez extraordinaire \[\text{Aire latérale du cône} = \pi a r\]On s’intéresse enfin à un autre solide apparenté : le cône tronqué (et où est la σφαίρα dans tout ça ? Patience…)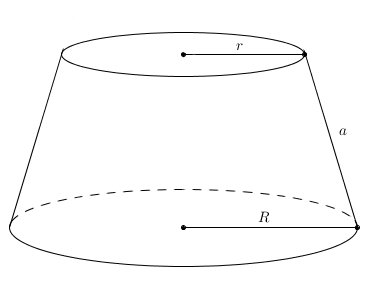 Voilà un cône tronqué dont la petite base a pour rayon \(r\) et la grande, \(R\). On notera \(a\) l’apothème du cône tronqué. Le meilleur moyen de retrouver une expression qui représente l’aire latérale d’un cône tronqué est de restituer le grand cône original.
Voilà un cône tronqué dont la petite base a pour rayon \(r\) et la grande, \(R\). On notera \(a\) l’apothème du cône tronqué. Le meilleur moyen de retrouver une expression qui représente l’aire latérale d’un cône tronqué est de restituer le grand cône original.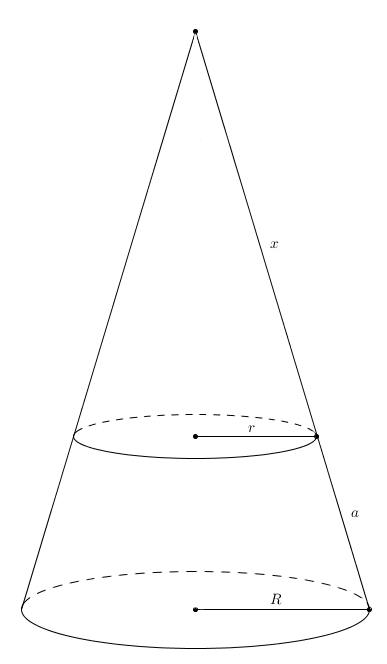 L’apothème de ce grand cône est \(x+a\) et on sait donc que l’aire latérale du grand cône est \[\pi R(x+a)\]Il suffit de soustraire l’aire latérale du cône d’apothème \(x\), celui qu’on enlève pour obtenir le cône tronqué. Son aire latérale étant \(\pi r x\), on obtient comme aire latérale du cône tronqué \begin{align*}\pi R (x+a)-\pi r x &=\pi R x + \pi R a-\pi r x \\ \\ &=\pi\left(Ra + (Rx-rx)\right)\end{align*}Le problème un peu gênant avec cette expression est qu’elle fait intervenir cette quantité fantôme, \(x\), qui ne fait pas partie du cône tronqué du départ. Est-il possible d’exprimer l’aire latérale du cône tronqué avec seulement les quantités du départ, à savoir \(r\), \(R\), et \(a\) ? C’est possible à l’aide de deux triangles semblables qu’on fait apparaître dans le grand cône restitué. Il suffit de tracer la hauteur du grand cône
L’apothème de ce grand cône est \(x+a\) et on sait donc que l’aire latérale du grand cône est \[\pi R(x+a)\]Il suffit de soustraire l’aire latérale du cône d’apothème \(x\), celui qu’on enlève pour obtenir le cône tronqué. Son aire latérale étant \(\pi r x\), on obtient comme aire latérale du cône tronqué \begin{align*}\pi R (x+a)-\pi r x &=\pi R x + \pi R a-\pi r x \\ \\ &=\pi\left(Ra + (Rx-rx)\right)\end{align*}Le problème un peu gênant avec cette expression est qu’elle fait intervenir cette quantité fantôme, \(x\), qui ne fait pas partie du cône tronqué du départ. Est-il possible d’exprimer l’aire latérale du cône tronqué avec seulement les quantités du départ, à savoir \(r\), \(R\), et \(a\) ? C’est possible à l’aide de deux triangles semblables qu’on fait apparaître dans le grand cône restitué. Il suffit de tracer la hauteur du grand cône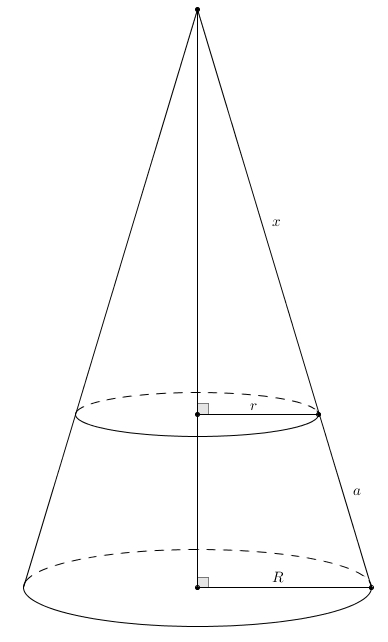 et on se retrouve avec lesdits triangles semblables (par AA, puisqu’ils sont rectangles et partagent l’angle aigu dont le sommet est l’apex du cône). Ainsi, on obtient la proportion \[\frac{x}{r} = \frac{x+a}{R}\]qui donne en effectuant le produit croisé \[Rx = rx + ra\]ou de manière équivalente \[Rx-rx = ra\]Ainsi il est possible de remplacer le \((Rx-rx)\) dans l’expression précédente afin d’obtenir une expression pour l’aire latérale du cône tronqué qui ne fait intervenir que les quantités \(r\), \(R\) et \(a\). On obtient \begin{align*}\pi\left(Ra+(Rx-rx)\right)&=\pi(Ra+ra) \\ \\ &=\pi a(R+r)\end{align*}Entre en scène l’incomparable mathématicien grec Archimède. Il s’attaque à la sphère. Or, contrairement au cône, tronqué ou non, ou au cylindre, la sphère n’est pas une surface développable. Archimède fera preuve d’une astuce magistrale pour calculer l’aire de la sphère.
et on se retrouve avec lesdits triangles semblables (par AA, puisqu’ils sont rectangles et partagent l’angle aigu dont le sommet est l’apex du cône). Ainsi, on obtient la proportion \[\frac{x}{r} = \frac{x+a}{R}\]qui donne en effectuant le produit croisé \[Rx = rx + ra\]ou de manière équivalente \[Rx-rx = ra\]Ainsi il est possible de remplacer le \((Rx-rx)\) dans l’expression précédente afin d’obtenir une expression pour l’aire latérale du cône tronqué qui ne fait intervenir que les quantités \(r\), \(R\) et \(a\). On obtient \begin{align*}\pi\left(Ra+(Rx-rx)\right)&=\pi(Ra+ra) \\ \\ &=\pi a(R+r)\end{align*}Entre en scène l’incomparable mathématicien grec Archimède. Il s’attaque à la sphère. Or, contrairement au cône, tronqué ou non, ou au cylindre, la sphère n’est pas une surface développable. Archimède fera preuve d’une astuce magistrale pour calculer l’aire de la sphère.

Il considère un cercle de rayon \(r\), de diamètre \(AA’\) et il y inscrit un polygone régulier de côté \(x\) possédant un nombre pair de côtés. Pour les besoins de la cause, on trace ici un octogone régulier \(ABCDA’D’C’B’\) mais le même raisonnement s’applique à n’importe quel polygone régulier possédant un nombre pair de côtés. Archimède trace ensuite les segment \(BB’\), \(CC’\) et \(DD’\), coupant le diamètre \(AA’\) respectivement en \(F\), \(G\) et \(H\). Il trace aussi les segments \(B’C\) et \(C’D\), coupant respectivement le diamètre \(AA’\) en \(K\) et \(L\). Enfin, il trace le (curieux) segment \(BA’\), dont on note pour l’instant la mesure par \(y\).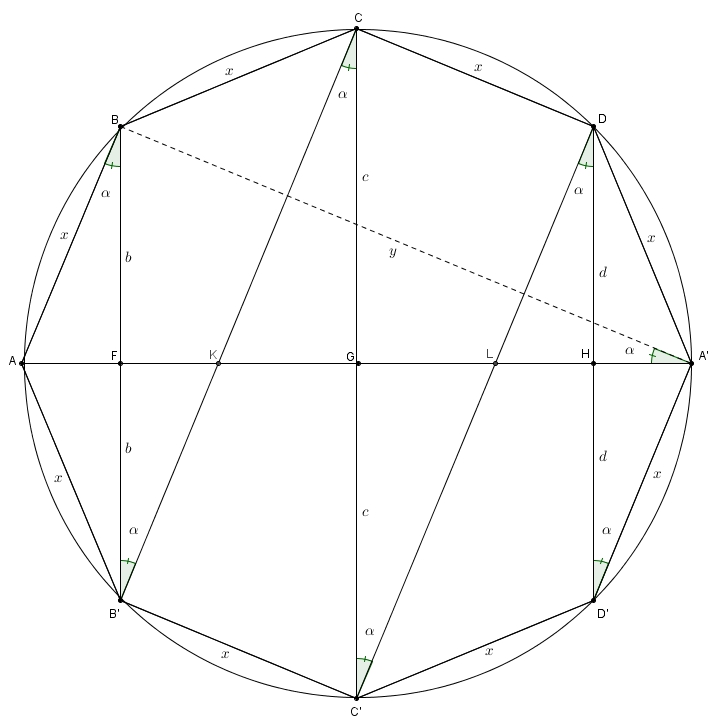 On a plusieurs segments isométriques : \(BF\) et \(B’F\), de longueur \(b\), \(CG\) et \(C’G\), de longueur \(c\) et \(DH\) et \(D’H\), de longueur \(d\). Par ailleurs, comme le polygone est régulier, les cordes \(AB\), \(BC\), \(CD\), etc. sont toutes isométriques et, incidemment, les arcs \(AB\), \(BC\), \(CD\), etc. sont tous isométriques. Plusieurs angles inscrit interceptent donc des arcs isométriques. C’est le cas notamment des angles \(BA’A\), \(ABB’\), \(BB’C\), \(B’CC’\), etc. Tous ces angles sont dénotés sur le schéma par \(\alpha\).
On a plusieurs segments isométriques : \(BF\) et \(B’F\), de longueur \(b\), \(CG\) et \(C’G\), de longueur \(c\) et \(DH\) et \(D’H\), de longueur \(d\). Par ailleurs, comme le polygone est régulier, les cordes \(AB\), \(BC\), \(CD\), etc. sont toutes isométriques et, incidemment, les arcs \(AB\), \(BC\), \(CD\), etc. sont tous isométriques. Plusieurs angles inscrit interceptent donc des arcs isométriques. C’est le cas notamment des angles \(BA’A\), \(ABB’\), \(BB’C\), \(B’CC’\), etc. Tous ces angles sont dénotés sur le schéma par \(\alpha\).
À l’instar de notre démarche avec Héron, on suit Archimède dans une galère de triangles semblables et de proportions. Les triangles \(ABA’\) et \(AFB\) sont semblables par AA : il possèdent tous les deux l’angle \(BAF\) et un angle \(\alpha\). On obtient donc \[\frac{m\overline{AF}}{b} = \frac{x}{y}\]ou \[\left(m\overline{AF}\right)y=xb\]Le triangle \(AFB\) est aussi semblable au triangle \(KFB’\) par AA : une paire d’angles isométriques opposés par le sommet et une paire d’angles \(\alpha\). On a \[\frac{m\overline{FK}}{b} = \frac{m\overline{AF}}{b} = \frac{x}{y}\]dans laquelle la dernière égalité provient de la proportion précédente, et avec le produit croisé on obtient \[\left(m\overline{FK}\right)y=xb\]La prochaine paire de triangles isométriques est celle-ci : les triangles \(KFB’\) et \(KGC\) par AA (une paire d’angles isométriques opposés par le sommet et une paire d’angles \(\alpha\)). On obtient comme proportion \[\frac{m\overline{KG}}{c} = \frac{m\overline{FK}}{b} = \frac{x}{y}\]dans laquelle la dernière égalité provient aussi de la proportion précédente. Avec le produit croisé on obtient cette fois-ci \[\left(m\overline{KG}\right)y=xc\]et on continue de la même manière à trouver des paires de triangles semblables. Le triangle \(KGC\) est à son tour semblable au triangle \(LGC’\), ce qui nous donne \[\left(m\overline{GL}\right)y=xc\]Le triangle \(LGC’\) est lui-même semblable au triangle \(LHD\) desquels on tire \[\left(m\overline{LH}\right)y=xd\]Enfin, la paire de triangles semblables \(LHD\) et \(A’HD’\) nous donne \[\left(m\overline{HA’}\right)y=xd\]Archimède additionne ensuite toutes ces équations\begin{align*}xb&=\left(m\overline{AF}\right)y \\ +\ xb &= \left(m\overline{FK}\right)y \\ + \ xc &=\left(m\overline{KG}\right)y \\ + \ xc &= \left(m\overline{GL}\right)y \\ + \ xd &=\left(m\overline{LH}\right)y \\ + \ xd &= \left(m\overline{HA’}\right)y\end{align*}afin d’obtenir \[2xb+2xc+2xd = \left(m\overline{AF}+m\overline{FK}+m\overline{KG}+m\overline{GL}+m\overline{LH}+m\overline{HA’}\right)y\]L’égalité précédente se simplifie de belle manière : \[x(2b + 2c+2d) = \left(m\overline{AA’}\right)y\]Qui plus est, le rayon du cercle étant \(r\), et \(AA’\) un diamètre, on a\[x(2b+2c+2d)=2ry\]Cette dernière équation joue un rôle primordial dans sa démarche. Archimède fait enfin apparaître une sphère. Il fait faire à toute la figure une rotation autour de l’axe \(AA’\). Alors que le cercle décrit une sphère, le polygone régulier, lui, décrit une série de cônes tronqués flanqués de deux cônes complets aux deux extrémités [1].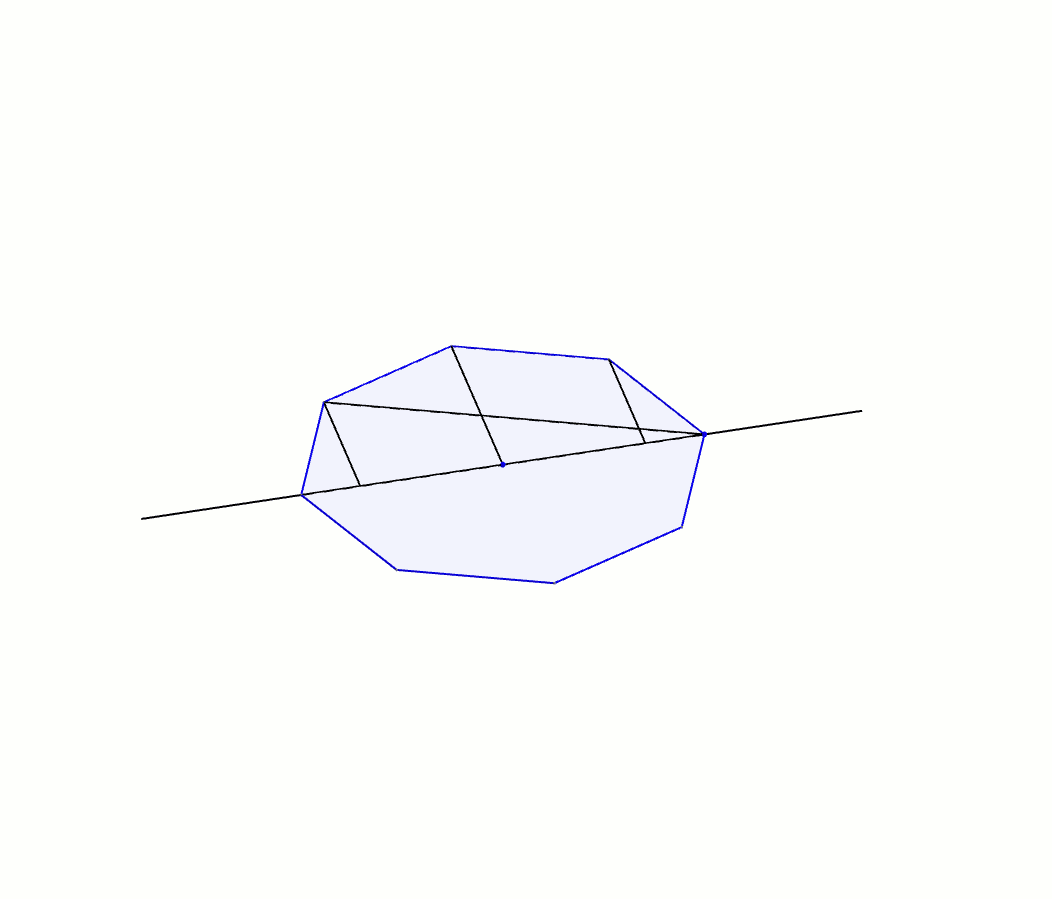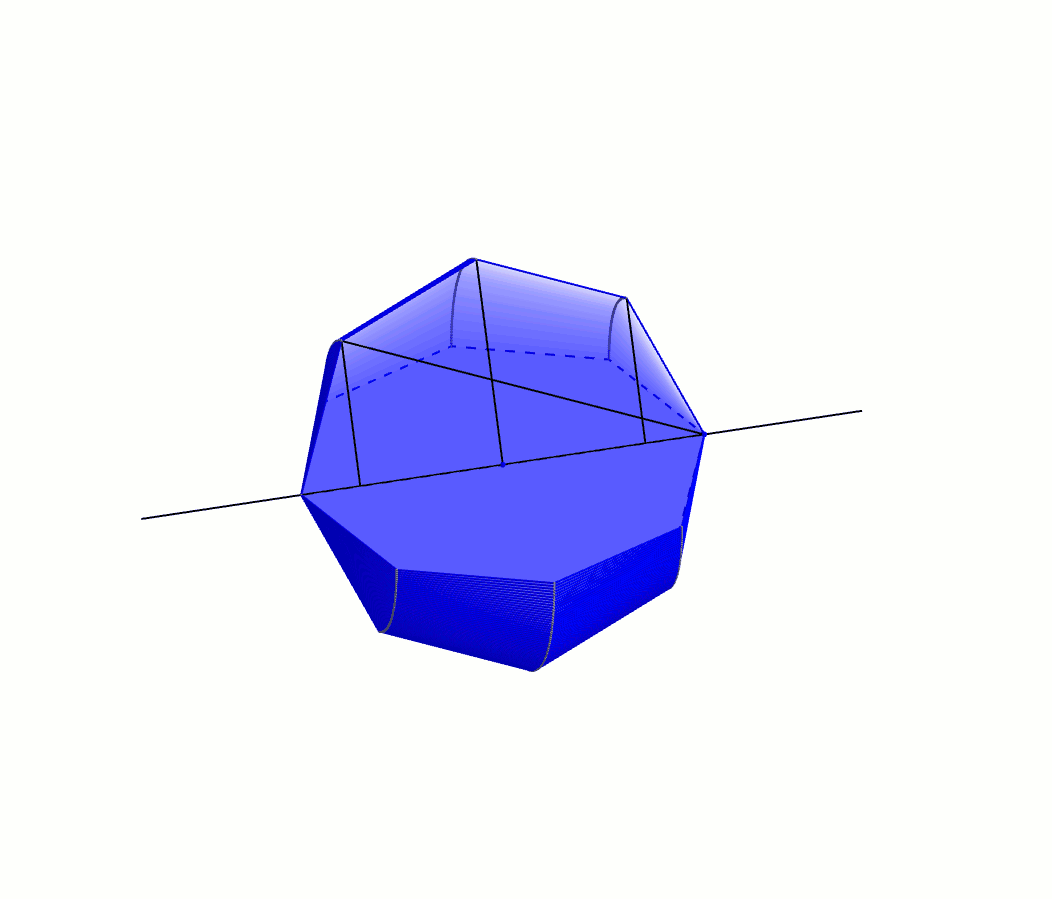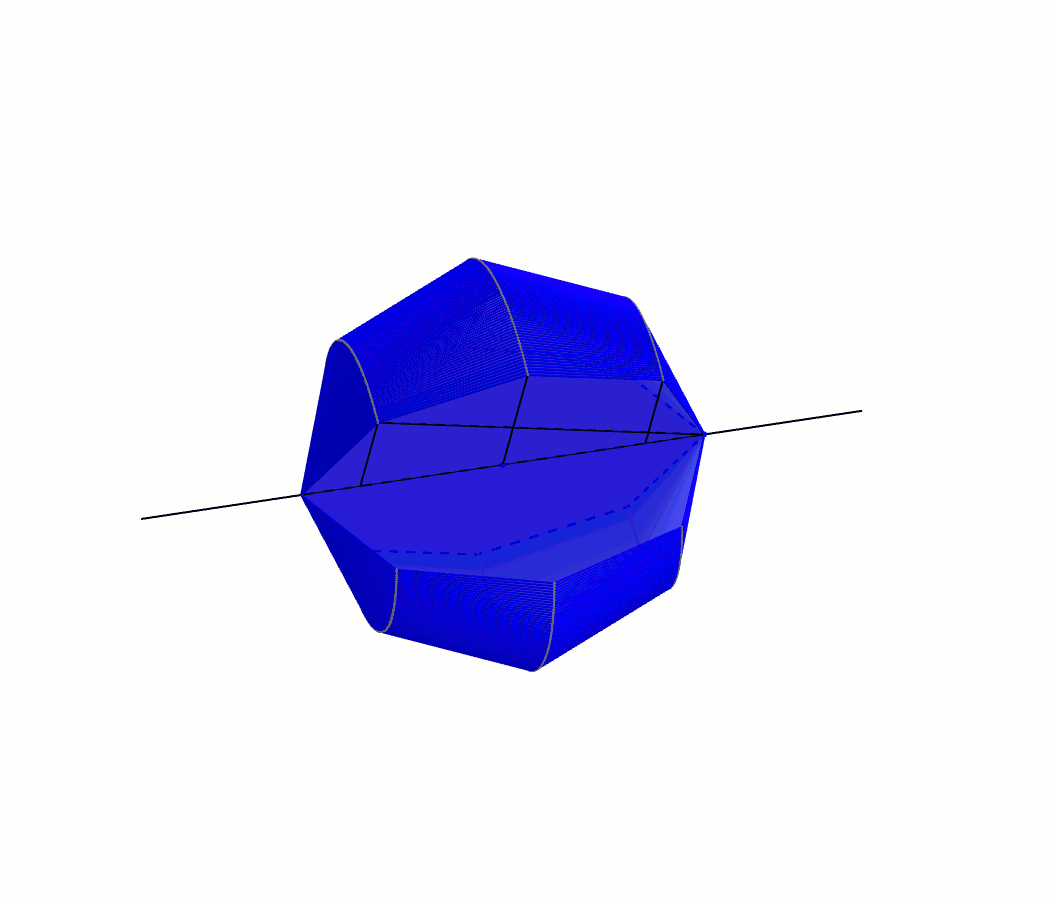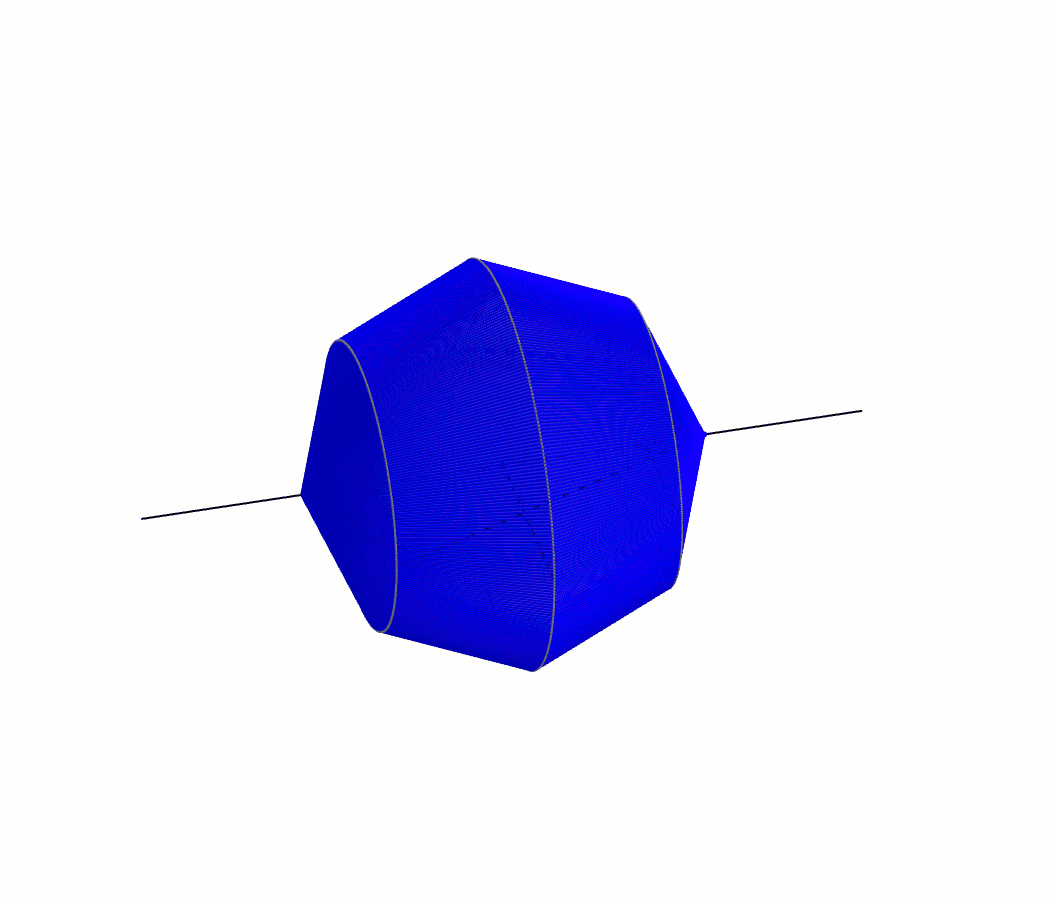
On note que les apothèmes des deux cônes et des cônes tronquées ont tous la même mesure : \(x\). Archimède peut donc maintenant déterminer l’aire totale de ce solide de révolution. Le rayon de la base du cône de gauche est \(b\) et donc son aire latérale est \(\pi x b\). Le cône tronqué adjacent possède un rayon de \(b\) pour la petite base, un rayon de \(c\) pour la grande base. Son aire latérale est donc \(\pi x (b+c)\). De la même manière, le cône tronqué à droite a pour aire latérale \(\pi x (c+d)\) et le cône à l’extrémité droite, \(\pi x d\). En combinant ces résultats, on obtient l’aire du solide \[\pi x b + \pi x (b+c) + \pi x (c + d) + \pi x d\]expression de laquelle on obtient\begin{align*}\pi x b + \pi x (b+c) + \pi x (c + d) + \pi x d &= \pi x b + \pi x b + \pi x c + \pi x c + \pi x d + \pi x d \\ \\ &= \pi x (2b + 2c + 2d)\end{align*}Ah ! Il devient à ce moment évident pourquoi Archimède avait introduit le segment mystérieux \(A’B\). On comprend aussi pourquoi il avait besoin d’un polygone régulier possédant un nombre pair de côtés. Cela lui permet de remplacer le membre de droite de l’expression. L’aire du solide est donc \[\pi x(2b + 2c + 2d) = \pi (2ry)\]Bien sûr, cette expression ne correspond pas à l’aire de la sphère, mais bien à l’aire d’un solide qui prétend être une approximation de la sphère. Or, l’approximation est d’autant meilleure que le polygone régulier du départ comporte un grand nombre de côtés. Archimède utilise donc 2000 ans avant son temps la notion de limite à travers sa technique du reductio ad absurdum. En langage moderne [2], il explique que lorsque le nombre de côtés du polygone régulier tend vers l’infini, l’aire du solide tend vers celui de la sphère !
En augmentant le nombre de côtés, il est clair que le rayon du cercle \(r\) ne change pas : cependant, la mesure \(y\), elle, change ! En effet, en augmentant le nombre de côtés, le point \(B\) se rapproche de \(A\) sur l’arc \(AB\), et de cette manière le segment \(A’B\) tend vers le diamètre (de mesure \(2r\)) du cercle. En d’autres mots lorsque le nombre de côtés du polygone régulier tend vers l’infini, \[m\overline{A’B} = y \to 2r\]Ainsi, lorsque le nombre de côtés du polygone régulier tend vers l’infini, l’aire du solide, qui tend vers celui de la sphère, est \[\pi (2ry) \to \pi (2r(2r)) = 4\pi r^{2}\]On voit souvent le nom d’Archimède nommé avec ceux de Gauss, Euler ou Newton comme étant les plus grands mathématiciens de tous les temps. J’espère que le présent billet ainsi que le précédent vous ont mieux fait apprécier (ou simplement découvrir) une toute petite parcelle de son œuvre.
[1]En utilisant un décagone, par exemple, ou un autre polygone dont le nombre de côtés ne se divise qu’une seule fois par \(2\), on obtiendrait un cylindre « central ». Le lecteur peut vérifier que la démarche fonctionne tout aussi bien en se rappelant le facteur \(2\) dans la formule de l’aire latérale du cylindre.
[2]En réalité, Archimède montre que lorsqu’on augmente le nombre de côtés du polygone, le solide ne peut avoir une aire totale plus grande que celle de la sphère. Il montre ensuite que lorsqu’on augmente le nombre de côtés du polygone, le solide ne peut avoir une aire plus petite que celle de la sphère (en considérant le cercle inscrit). Conclusion : le résultat obtenu correspond à l’aire de la sphère. Et il ne faut pas oublier, bien sûr, qu’il n’y a pas que le reductio ad absurdum qui diffère. Archimède ne réfléchie qu’en termes géométriques : il parle de grands cercles (l’aire de la sphère correspond à quatre fois l’aire d’un de ses grands cercles). On n’y voit aucune trace d’algèbre. La description de ses travaux ci-dessus est adaptée, traduite dans un langage et un style moderne.
Référence : William Dunham (1994), The Mathematical Universe


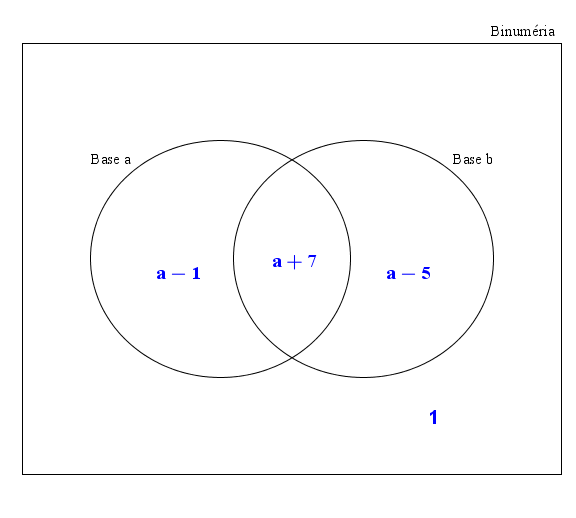 On peut donc trouver la valeur de \(a\) en faisant la somme des habitants de Binuméria à partir des différentes régions du diagramme de Venn ci-dessus\[(a-1)+(a+7)+(a-5)+1=3a+2\]Cette expression représente le même nombre que le total déjà annoncé par Bob \[3a + 2 = 2a + 13\]ce qui nous donne la base d’Alice \[a = 11\]et aussi la base de Bob\begin{align*}b&=a+4 \\ \\ &=11+4 \\ \\ &=15\end{align*}On peut enfin répondre à la question ! Il y a \[2(11)+13=2(15)+5 =35\]personnes qui vivent à Binuméria !
On peut donc trouver la valeur de \(a\) en faisant la somme des habitants de Binuméria à partir des différentes régions du diagramme de Venn ci-dessus\[(a-1)+(a+7)+(a-5)+1=3a+2\]Cette expression représente le même nombre que le total déjà annoncé par Bob \[3a + 2 = 2a + 13\]ce qui nous donne la base d’Alice \[a = 11\]et aussi la base de Bob\begin{align*}b&=a+4 \\ \\ &=11+4 \\ \\ &=15\end{align*}On peut enfin répondre à la question ! Il y a \[2(11)+13=2(15)+5 =35\]personnes qui vivent à Binuméria ! La hauteur du rectangle correspond à la hauteur du cylindre et sa base, à la circonférence du cercle. Ainsi, un cylindre de hauteur \(h\) et dont le rayon de la base est \(r\) aura une aire latérale de \(2\pi rh\). On considère aussi un cône de rayon \(r\) et d’apothème \(a\)
La hauteur du rectangle correspond à la hauteur du cylindre et sa base, à la circonférence du cercle. Ainsi, un cylindre de hauteur \(h\) et dont le rayon de la base est \(r\) aura une aire latérale de \(2\pi rh\). On considère aussi un cône de rayon \(r\) et d’apothème \(a\)
 Voilà un cône tronqué dont la petite base a pour rayon \(r\) et la grande, \(R\). On notera \(a\) l’apothème du cône tronqué. Le meilleur moyen de retrouver une expression qui représente l’aire latérale d’un cône tronqué est de restituer le grand cône original.
Voilà un cône tronqué dont la petite base a pour rayon \(r\) et la grande, \(R\). On notera \(a\) l’apothème du cône tronqué. Le meilleur moyen de retrouver une expression qui représente l’aire latérale d’un cône tronqué est de restituer le grand cône original. L’apothème de ce grand cône est \(x+a\) et on sait donc que l’aire latérale du grand cône est \[\pi R(x+a)\]Il suffit de soustraire l’aire latérale du cône d’apothème \(x\), celui qu’on enlève pour obtenir le cône tronqué. Son aire latérale étant \(\pi r x\), on obtient comme aire latérale du cône tronqué \begin{align*}\pi R (x+a)-\pi r x &=\pi R x + \pi R a-\pi r x \\ \\ &=\pi\left(Ra + (Rx-rx)\right)\end{align*}Le problème un peu gênant avec cette expression est qu’elle fait intervenir cette quantité fantôme, \(x\), qui ne fait pas partie du cône tronqué du départ. Est-il possible d’exprimer l’aire latérale du cône tronqué avec seulement les quantités du départ, à savoir \(r\), \(R\), et \(a\) ? C’est possible à l’aide de deux triangles semblables qu’on fait apparaître dans le grand cône restitué. Il suffit de tracer la hauteur du grand cône
L’apothème de ce grand cône est \(x+a\) et on sait donc que l’aire latérale du grand cône est \[\pi R(x+a)\]Il suffit de soustraire l’aire latérale du cône d’apothème \(x\), celui qu’on enlève pour obtenir le cône tronqué. Son aire latérale étant \(\pi r x\), on obtient comme aire latérale du cône tronqué \begin{align*}\pi R (x+a)-\pi r x &=\pi R x + \pi R a-\pi r x \\ \\ &=\pi\left(Ra + (Rx-rx)\right)\end{align*}Le problème un peu gênant avec cette expression est qu’elle fait intervenir cette quantité fantôme, \(x\), qui ne fait pas partie du cône tronqué du départ. Est-il possible d’exprimer l’aire latérale du cône tronqué avec seulement les quantités du départ, à savoir \(r\), \(R\), et \(a\) ? C’est possible à l’aide de deux triangles semblables qu’on fait apparaître dans le grand cône restitué. Il suffit de tracer la hauteur du grand cône et on se retrouve avec lesdits triangles semblables (par AA, puisqu’ils sont rectangles et partagent l’angle aigu dont le sommet est l’apex du cône). Ainsi, on obtient la proportion \[\frac{x}{r} = \frac{x+a}{R}\]qui donne en effectuant le produit croisé \[Rx = rx + ra\]ou de manière équivalente \[Rx-rx = ra\]Ainsi il est possible de remplacer le \((Rx-rx)\) dans l’expression précédente afin d’obtenir une expression pour l’aire latérale du cône tronqué qui ne fait intervenir que les quantités \(r\), \(R\) et \(a\). On obtient \begin{align*}\pi\left(Ra+(Rx-rx)\right)&=\pi(Ra+ra) \\ \\ &=\pi a(R+r)\end{align*}Entre en scène l’incomparable mathématicien grec Archimède. Il s’attaque à la sphère. Or, contrairement au cône, tronqué ou non, ou au cylindre, la sphère n’est pas une surface développable. Archimède fera preuve d’une astuce magistrale pour calculer l’aire de la sphère.
et on se retrouve avec lesdits triangles semblables (par AA, puisqu’ils sont rectangles et partagent l’angle aigu dont le sommet est l’apex du cône). Ainsi, on obtient la proportion \[\frac{x}{r} = \frac{x+a}{R}\]qui donne en effectuant le produit croisé \[Rx = rx + ra\]ou de manière équivalente \[Rx-rx = ra\]Ainsi il est possible de remplacer le \((Rx-rx)\) dans l’expression précédente afin d’obtenir une expression pour l’aire latérale du cône tronqué qui ne fait intervenir que les quantités \(r\), \(R\) et \(a\). On obtient \begin{align*}\pi\left(Ra+(Rx-rx)\right)&=\pi(Ra+ra) \\ \\ &=\pi a(R+r)\end{align*}Entre en scène l’incomparable mathématicien grec Archimède. Il s’attaque à la sphère. Or, contrairement au cône, tronqué ou non, ou au cylindre, la sphère n’est pas une surface développable. Archimède fera preuve d’une astuce magistrale pour calculer l’aire de la sphère.


