S’il s’est écoulé pas mal de temps avant que j’écrive un nouveau billet, c’est qu’un petit problème génial a occupé une grande partie de mon temps libre. En effet, il se trouve qu’un de mes collègues a une passion pour les mathématiques toute aussi forte que la mienne. Voici le problème qu’il m’a envoyé la semaine dernière. Un problème simple (et connu) mais dont la solution s’avère, on s’en doute, plutôt ardue. Il s’agit de compter le nombre de triangles équilatéraux que l’on retrouve dans un grand triangle équilatéral de côté \(n\).
Pour \(n=1\)
\(n=2\)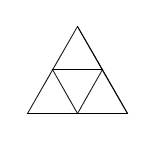 \(n=3\)
\(n=3\)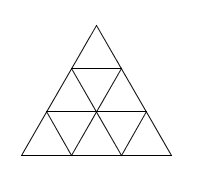 \(n=4\)
\(n=4\)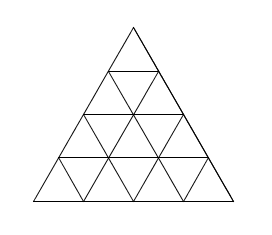 \(n=5\)
\(n=5\)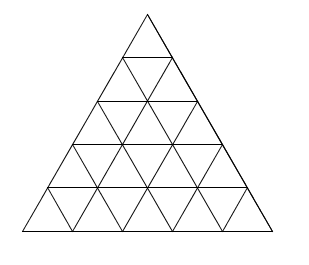 \(n=6\)
\(n=6\)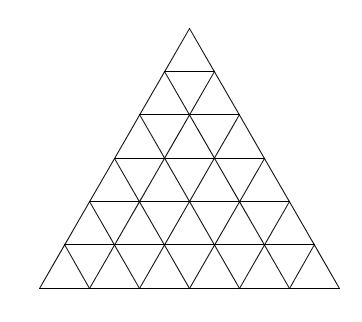 Et comme je n’ai trouvé nulle part sur Internet les images des triangles pour les valeurs de \(n\) subséquentes, et que de tracer ces triangles à la main est une tâche plutôt ingrate, et que si vous êtes comme moi vous voudrez sûrement dénombrer vous aussi, on a pour \(n=7\)
Et comme je n’ai trouvé nulle part sur Internet les images des triangles pour les valeurs de \(n\) subséquentes, et que de tracer ces triangles à la main est une tâche plutôt ingrate, et que si vous êtes comme moi vous voudrez sûrement dénombrer vous aussi, on a pour \(n=7\)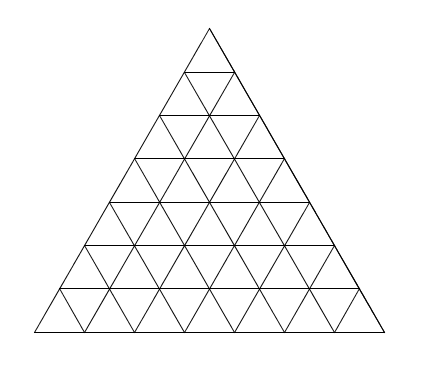 \(n=8\)
\(n=8\)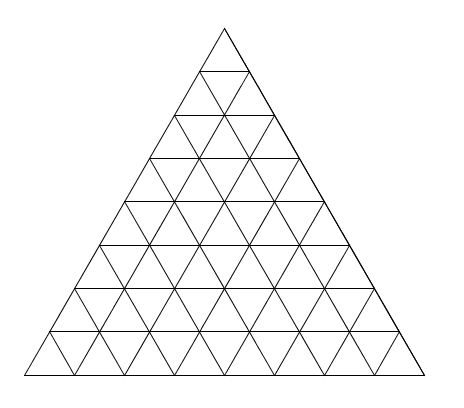 \(n=9\)
\(n=9\)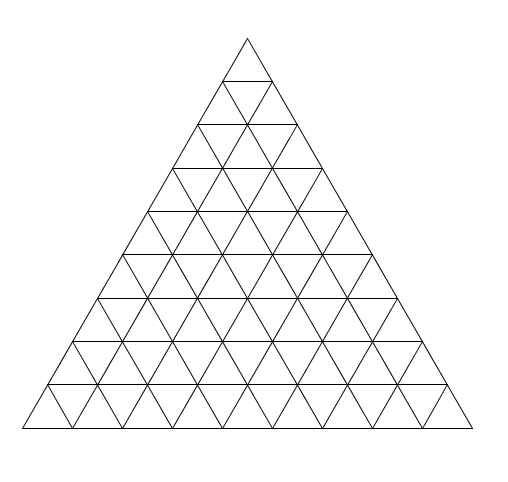 et enfin \(n=10\)
et enfin \(n=10\) Non sans effort, vous trouverez peut-être ces résultats :
Non sans effort, vous trouverez peut-être ces résultats :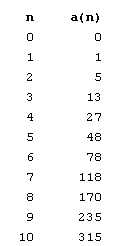
où \(a(n)\) est le nombre de triangles dans chaque figure. Ce qui me frappe d’abord et avant tout c’est… qu’il n’y a effectivement rien de frappant dans les nombres de la colonne de droite. On ne semble déceler aucune régularité évidente (outre que le nombre de petits triangles d’une unité de côté est toujours égal à \(n^{2}\)). Il faut donc chercher plus loin. On remarque, lors du dénombrement, qu’il y a quelque chose qui s’avère différent si le nombre \(n\) est pair ou impair. Mais il ne s’agit, à cette étape-ci, que d’une conjecture. D’ailleurs, en ne considérant dans le tableau précédent que les valeurs de \(n\) paires (ou impaires), on peut constater que les accroissements entre les accroissements entre les accroissements sont constants (vous trouverez que les accroissements entre les accroissements entre les accroissements valent tous \(12\)). On peut donc espérer pour l’instant que la ou les règles recherchées soient des polynômes du troisième degré.
Lorsqu’on compte le nombre de triangles, on tient compte du nombre de triangles des différentes grosseurs. Par exemple, en considérant \(n=5\)
 on s’aperçoit qu’il contient \(25\) petits triangles de une unité de côté. Il contient aussi \(13\) plus grands triangles de \(2\) unités de côté (ou composés de \(4\) petits triangles). Il contient \(6\) triangles encore plus grands de \(3\) unités de côté (ou composés de \(9\) petits triangles). Il contient \(3\) grands triangles de quatre unités de côté (ou composés de \(16\) petits triangles) et finalement \(1\) triangle de \(5\) unités de côté (ou composé de \(25\) petits triangles). On obtient bien \[25 + 13 + 6 + 3 + 1 = 48\]Non sans effort, vous pourrez construire le tableau suivant pour les premières valeurs de \(n\) (en comptant séparément les plus petits triangles de côté \(k\)) :
on s’aperçoit qu’il contient \(25\) petits triangles de une unité de côté. Il contient aussi \(13\) plus grands triangles de \(2\) unités de côté (ou composés de \(4\) petits triangles). Il contient \(6\) triangles encore plus grands de \(3\) unités de côté (ou composés de \(9\) petits triangles). Il contient \(3\) grands triangles de quatre unités de côté (ou composés de \(16\) petits triangles) et finalement \(1\) triangle de \(5\) unités de côté (ou composé de \(25\) petits triangles). On obtient bien \[25 + 13 + 6 + 3 + 1 = 48\]Non sans effort, vous pourrez construire le tableau suivant pour les premières valeurs de \(n\) (en comptant séparément les plus petits triangles de côté \(k\)) :

Et pourtant, encore une fois, aucune régularité ne semble transparaître (enfin pour moi…) J’ai soumis ce problème à mes élèves (pour leur montrer qu’un problème simple peut avoir une solution loin d’être triviale) et un de ceux-ci est venu me voir avec ses calculs. Il avait fait un tableau semblable au miens mais n’avait compté (par mégarde) que les triangles « à l’endroit », c’est-à-dire ceux qui pointent vers le haut. Ah! Erreur d’un élève ? Nouvelle piste ? Il s’avère que décomposer le problème en un problème de « nombre triangles pointant vers le haut » et « nombre triangles pointant vers le bas » (plutôt que « nombre de triangles de \(k\) unités de côté ») s’avère drôlement fructueux.
Le tableau précédant devient plutôt

Nous allons définir la fonction a comme suit : \[a(n) = u(n) + v(n)\]dans laquelle \(u\) donne le nombre de triangles pointant vers le haut et \(v\) le nombre de triangles pointant vers le bas.
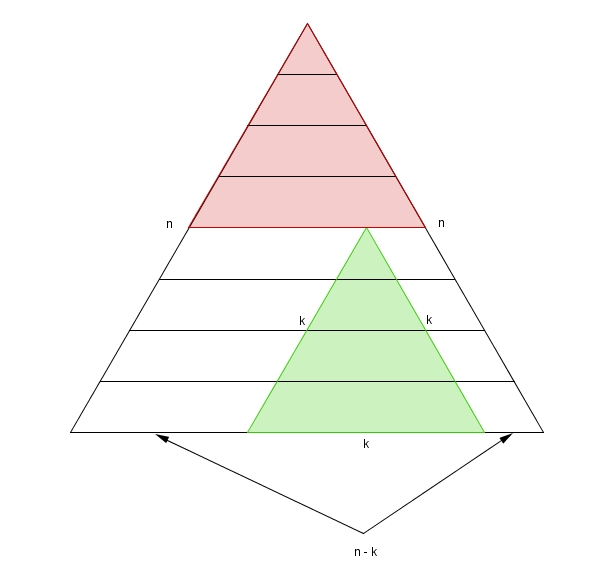
Considérons le petit triangle de côté \(k\) pointant vers le haut dans ce triangle de côté \(n\).
Le sommet du triangle de côté \(k\) doit obligatoirement être dans la région rougeâtre sur le schéma. Il y a donc un seul triangle à partir du haut, deux sur l’étage immédiatement inférieur, trois sur le suivant et ce jusqu’à au dernier étage. Mais, justement, combien y a-t-il de ces triangles au dernier étage ? En comptant bien, on trouve \[n-k+1\]triangles possibles. Pour un \(k\) et un \(n\) donnés, il y a donc \[1 + 2 + 3 + 4 + 5+ \ \dots \ + (n-k+1)\]triangles, ce qui se somme à \[\frac{(n-k+1)(n-k+1+1)}{2}\]ou plus simplement \[\frac{(n-k+1)(n-k+2)}{2}\]Maintenant, quelle est la valeur maximale de \(k\) ? Bien sûr, c’est \(n\). On obtient donc \[u(n) = \sum_{k=1}^{n}\frac{(n-k+1)(n-k+2)}{2}\]ce qui fait en développant \[u(n) = \sum_{k=1}^{n}\frac{n^{2}+3n + 2 + k^{2}-2kn -3k}{2}\]puis en sortant le facteur \(\frac{1}{2}\) de la sommation \[u(n) = \frac{1}{2}\sum_{k=1}^{n}n^{2}+3n + 2 + k^{2}-2kn-3k\]On obtient dans un premier temps \[u(n) = \frac{1}{2}\left(n^{3}+3n^{2}+2n + \sum_{k=1}^{n}k^{2}-2n\sum_{k=1}^{n}k-3\sum_{k=1}^{n}k\right)\]puis, en se rappelant ceci, on obtient dans un deuxième temps \[u(n) = \frac{1}{2}\left(n^{3}+3n^{2}+2n + \frac{n(n+1)(2n+1)}{6}-2n\left(\frac{n(n+1)}{2}\right)-3\left(\frac{n(n+1)}{2}\right)\right)\]Suivent ces quelques étapes dans lesquelles on simplifie le tout. D’abord \[u(n) = \frac{1}{2}\left(n^{3}+3n^{2}+2n +\frac{n(n+1)(2n+1)}{6}-n^{3}-n^{2}-\frac{3n^{2}}{2}-\frac{3n}{2}\right)\]puis \[u(n) = n^{2}+n + \frac{n(n+1)(2n+1)}{12}-\frac{3n^{2}}{4}-\frac{3n}{4}\]En mettant sur dénominateur commun \[u(n) = \frac{12n^{2}}{12}+\frac{12n}{12} + \frac{n(n+1)(2n+1)}{12}-\frac{9n^{2}}{12}-\frac{9n}{12}\]et en développant \[u(n) = \frac{12n^{2}+12n + 2n^{3}+3n^{2}+n-9n^{2}-9n}{12}\]on obtient \[u(n)=\frac{2n^{3}+6n^{4}+4n}{12}\]et finalement en divisant les numérateur et dénominateur par \(2\) \[u(n) = \frac{n^{3}+3n^{2}+2n}{6}\]Voilà donc l’expression qui nous donne le nombre de triangle pointant vers le haut. Il reste à trouver \(v(n)\) On considère le petit triangle de côté \(k\) pointant vers le bas dans ce triangle de côté \(n\).
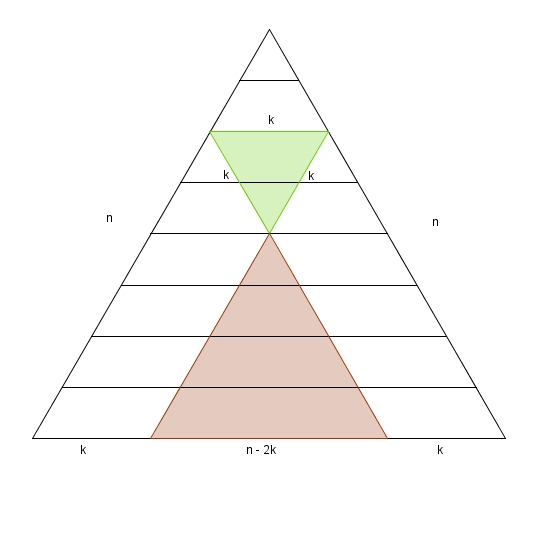 Encore une fois, le sommet du triangle de k unités de côté doit obligatoirement se trouver dans la région rougeâtre sur le schéma. Et, encore une fois, il y a un triangle possible à partir du haut, deux sur l’étage suivant, trois sur celui qui suit, et ce jusqu’au dernier étage. Ici, au dernier étage, il y aura toujours \[n-2k+1\]triangles possibles. Cela signifie que pour un \(k\) et un \(n\) donnés, il y aura donc \[1+2+3+4+ \ \dots \ +(n-2k+1)\]triangles, ce qui se somme à \[\frac{(n-2k+1)(n-2k+1+1)}{2}\]ou plus simplement\[\frac{(n-2k+1)(n-2k+2)}{2}\]Maintenant, quelle est la valeur maximale de \(k\) ? Dans le cas d’un \(n\) pair, il est facile de voir que ce sera \(\frac{n}{2}\). Dans le cas d’un \(n\) impair, ce sera plutôt \(\frac{n-1}{2}\). Voilà où se trouvait la différence entre les \(n\) pairs et impairs pressentie à l’étape préliminaire du dénombrement.
Encore une fois, le sommet du triangle de k unités de côté doit obligatoirement se trouver dans la région rougeâtre sur le schéma. Et, encore une fois, il y a un triangle possible à partir du haut, deux sur l’étage suivant, trois sur celui qui suit, et ce jusqu’au dernier étage. Ici, au dernier étage, il y aura toujours \[n-2k+1\]triangles possibles. Cela signifie que pour un \(k\) et un \(n\) donnés, il y aura donc \[1+2+3+4+ \ \dots \ +(n-2k+1)\]triangles, ce qui se somme à \[\frac{(n-2k+1)(n-2k+1+1)}{2}\]ou plus simplement\[\frac{(n-2k+1)(n-2k+2)}{2}\]Maintenant, quelle est la valeur maximale de \(k\) ? Dans le cas d’un \(n\) pair, il est facile de voir que ce sera \(\frac{n}{2}\). Dans le cas d’un \(n\) impair, ce sera plutôt \(\frac{n-1}{2}\). Voilà où se trouvait la différence entre les \(n\) pairs et impairs pressentie à l’étape préliminaire du dénombrement.
Pour une valeur de \(n\) paire
On trouve : \[v(n) = \sum_{k=1}^{\frac{n}{2}}\frac{(n-2k+1)(n-2k+2)}{2}\]ce qui fait en sortant le facteur \(\frac{1}{2}\) de la sommation \[v(u) = \frac{1}{2}\sum_{k=1}^{\frac{n}{2}}(n-2k+1)(n-2k+2)\]et en développant \[v(n) = \frac{1}{2}\sum_{k=1}^{\frac{n}{2}}n^{2}+3n+2+4k^{2}-4kn-6k\]On obtient alors dans un premier temps \[u(n) = \frac{1}{2}\left(\frac{n^{3}}{2}+\frac{3n^{2}}{2}+\frac{2n}{2}+4\sum_{k=1}^{\frac{n}{2}}k^{2}-4n\sum_{k=1}^{\frac{n}{2}}k-6\sum_{k=1}^{\frac{n}{2}}k\right)\] puis \[v(n) = \frac{1}{2}\left(\frac{n^{3}}{2}+\frac{3n^{2}}{2}+\frac{2n}{2}+4\cdot \frac{\frac{n}{2}\left(\frac{n}{2}+1\right)\left(2 \cdot \frac{n}{2} + 1\right)}{6}-4n\cdot \frac{\frac{n}{2}\left(\frac{n}{2}+1\right)}{2}-6\cdot\frac{\frac{n}{2}\left(\frac{n}{2}+1\right)}{2}\right)\]En développant davantage et simplifiant un peu on obtient \[v(n) = \frac{n^{3}}{4}+\frac{3n^{2}}{4}+\frac{2n}{4}+\frac{n^{3}+3n^{2}+2n}{12}-\frac{n^{3}+2n^{2}}{4}-\frac{3n^{2}+6n}{8}\]ce qui fait \[v(n) = \frac{n^{3}}{4}+\frac{3n^{2}}{4}+\frac{2n}{4}+\frac{n^{3}}{12}+\frac{3n^{2}}{12}+\frac{2n}{12}-\frac{n^{3}}{4}-\frac{2n^{2}}{4}-\frac{3n^{2}}{8}-\frac{6n}{8}\]En mettant sur dénominateur commun \[v(n) = \frac{6n^{3}}{24}+\frac{18n^{2}}{24}+\frac{12n}{24}+\frac{2n^{3}}{24}+\frac{6n^{2}}{24}+\frac{4n}{24}-\frac{6n^{3}}{24}-\frac{12n^{2}}{24}-\frac{9n^{2}}{24}-\frac{18n}{24}\]et en regroupant les termes semblables on trouve finalement \[v(n) = \frac{2n^{3}+3n^{2}-2n}{24}\]Cette expression nous donne le nombre de triangles pointant vers le bas pour un \(n\) pair.
Pour une valeur de \(n\) impaire
Dans ce cas, on aurait plutôt \[v(n) = \sum_{k=1}^{\frac{n-1}{2}}\frac{(n-2k+1)(n-2k+2)}{2}\]ce qui fait en sortant le facteur \(\frac{1}{2}\) de la sommation \[v(n) = \frac{1}{2}\sum_{k=1}^{\frac{n-1}{2}}(n-2k+1)(n-2k+2)\]et en développant \[v(n) = \frac{1}{2}\sum_{k=1}^{\frac{n-1}{2}}n^{2}+3n+2+4k^{2}-4kn-6k\]Dans un premier temps, on a \[v(n) = \frac{1}{2}\left(\frac{(n-1)(n^{2})}{2}+\frac{(n-1)(3n)}{2}+\frac{(n-1)(2)}{2}+4\sum_{k=1}^{\frac{n-1}{2}}k^{2}-4n\sum_{k=1}^{\frac{n-1}{2}}k-6\sum_{k=1}^{\frac{n-1}{2}}k\right)\]et dans un deuxième \[v(n) = \frac{1}{2}\left(\frac{n^{3}-n^{2}}{2}+\frac{3n^{2}-3n}{2}+\frac{2n-2}{2}+4\cdot \frac{\frac{n-1}{2}\left(\frac{n-1}{2}+1\right)\left(2\cdot \frac{n-1}{2}+1\right)}{6}-4n\cdot \frac{\frac{n-1}{2}\left(\frac{n-1}{2}+1\right)}{2}-6\cdot \frac{\frac{n-1}{2}\left(\frac{n-1}{2}+1\right)}{2}\right)\]En développant davantage et simplifiant un peu, on obtient \[v(n) = \frac{n^{3}-n^{2}}{4}+\frac{3n^{2}-3n}{4}+\frac{2n-2}{4}+\frac{n^{3}-n}{12}-\frac{n^{3}-n}{4}-\frac{3n^{2}-3}{8}\]puis \[v(n) = \frac{n^{3}}{4}-\frac{n^{2}}{4}+\frac{3n^{2}}{4}-\frac{3n}{4}+\frac{2n}{4}-\frac{2}{4}+\frac{n^{3}}{12}-\frac{n}{12}-\frac{n^{3}}{4}+\frac{n}{4}-\frac{3n^{2}}{8}+\frac{3}{8}\]en mettant sur dénominateur commun \[v(n) = \frac{6n^{3}}{24}-\frac{6n^{2}}{24}+\frac{18n^{2}}{24}-\frac{18n}{24}+\frac{12n}{24}-\frac{12}{24}+\frac{2n^{3}}{24}-\frac{2n}{24}-\frac{6n^{3}}{24}+\frac{6n}{24}-\frac{9n^{2}}{24}+\frac{9}{24}\]et en regroupant les termes semblables \[v(n) = \frac{2n^{3}+3n^{2}-2n-3}{24}\]Voilà ! Cette expression nous donne le nombre de triangles pointant vers le bas pour un \(n\) impair.
Le nombre de triangles au total
Il suffit maintenant de combiner ces résultats afin d’obtenir \(a(n)\). On a \[a(n) = u(n) + v(n)\]Dans le cas d’un \(n\) pair, on obtient \[a(n) = \frac{n^{3}+3n^{2}+2n}{6}+\frac{2n^{3}+3n^{2}-2n}{24}\]ce qui fait, en mettant sur dénominateur commun \[a(n) = \frac{4n^{3}+12n^{2}+8n}{24}+\frac{2n^{3}+3n^{2}-2n}{24}\]puis en regroupant les termes semblables \[a(n) = \frac{6n^{3}+15n^{2}+6n}{24}\]Finalement en divisant par \(3\) en haut et en bas, on obtient \[a(n) = \frac{2n^{3}+5n^{2}+2n}{8}\]toujours pour un \(n\) pair. Pour un \(n\) impair on a plutôt \[a(n) = \frac{n^{3}+3n^{2}+2n}{6} + \frac{2n^{3}+3n^{2}-2n-3}{24}\]ce qui fait, en mettant sur dénominateur commun \[a(n) = \frac{4n^{3}+12n^{2}+8n}{24}+\frac{2n^{3}+3n^{2}-2n-3}{24}\]puis en regroupant les termes semblables \[a(n) = \frac{6n^{3}+15n^{2}+6n-3}{24}\]Finalement, en divisant par \(3\) en haut et en bas, on obtient \[a(n) = \frac{2n^{3}+5n^{2}+2n-1}{8}\]pour un \(n\) impair.
Référence : http://mathforum.org/library/drmath/view/54369.html (En résolution de problèmes, il faut parfois étudier un problème connexe moins complexe pour avancer).
Juste .. Bravo.
Vraiment impressionnant, les maths me passionne mais je ne serai arrivé jusque là. Félicitation et chapeau quoi voilà
Bonjour,
C’est toujours excitant de se confronter à des problèmes en apparence simples. Bravo pour le courage et la patience.
J’ai trouvé une formule en utilisant 6 triangles pour différencier pair et impair. Elle regroupe toutes tailles et je la trouve esthétique.
Etude intéressante.
Mais au final plus simple de retenir que pour tout n on prend la partie entière de
n(n+1)(2n+1)/8
Erratum ! c’est [n(n+2)(2n+1)/8]
J’ai aussi résolu le probleme mais avec une autre méthoe plus simple (je crois) basé sur la recurence N(2k+3) – N(2k+1). J’ai donc écrit une formule un peut plus unifié
(4n^3+10n^2+4n+(-1)^n – 1)/16
N(n) étant bien sur le nombre totale de triangles
Ta dernière proposition pour l’unification ne marche pas pour les n impair, tu devrais dire l’arrondi entier et non partie entiere, (je crois)
Donc c’est E(n(n+2)(2n+1)/8)+1, tu a oublié le +1, ou tu devrait dire arrondi a l’entier sup
Haannn ! Ok ! Excuse, c’est moi qui ai mal calculé. Merci
Lire le thème 84, pages 172 et 173 du livre “Des Olympiades à l’Agrégation” Editions Ellipses (France) 1997 de Maurice Protat.