Voici une méthode pour trisecter un segment. Il en existe plusieurs, et même des méthodes requérant moins d’étapes mais voici probablement la plus connue. Ce qui nous est donné : le segment \(AB\).
On trace le cercle de centre \(A\) et de rayon \(\overline{AB}\). On trace ensuite le cercle de centre \(B\) et et de rayon \(\overline{AB}\). Ces deux cercles se croisent à deux endroits : appelons-les \(C\) et \(D\). Traçons le cercle de centre \(C\) et de rayon \(\overline{AC}\). Notons au passage que ce cercle passe aussi par \(B\) et que\[m\overline{AC}=m\overline{AB}\](c”est la méthode de construction d’un triangle équilatéral, Proposition 1 du Livre 1 des Éléments d’Euclide). On trace ensuite la droite \(AC\) qui coupe le cercle de centre \(C\) en \(A\) (évidemment) mais aussi en \(E\). On trace la droite \(DE\). Cette dernière coupe \(\overline{AB}\) en \(F\). Voilà ! On a \[m\overline{BF}=\frac{1}{3}m\overline{AF}\]
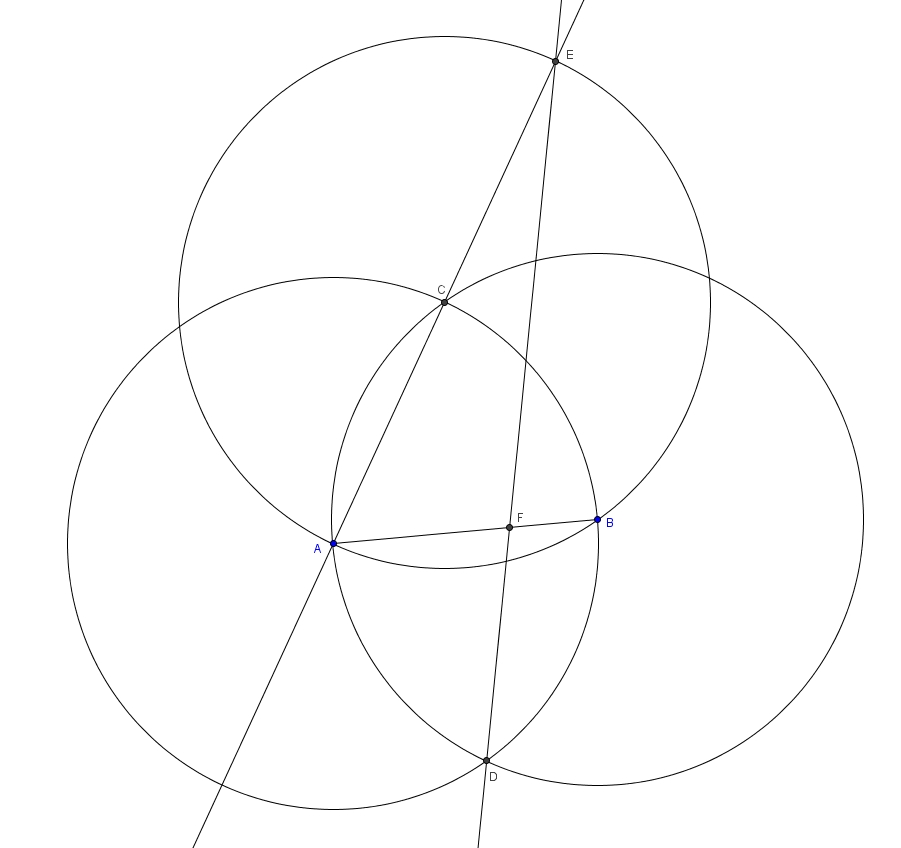 Notons d’abord que les trois cercles sont isométriques puisque la mesure de leur rayon est égale à la mesure du segment \(AB\). Considérons les triangles \(ABC\) et \(ABD\). Ce sont des triangles équilatéraux (chacun de leurs côtés est, justement, un rayon des trois cercles congrus). Les angles intérieurs d’un triangle équilatéral sont tous de \(60^{\circ}\). En particulier, les angles \(BAC\) et \(ABD\) valent tous les deux \(60^{\circ}\). \[m\angle BAC = m\angle ABD = 60^{\circ}\]
Notons d’abord que les trois cercles sont isométriques puisque la mesure de leur rayon est égale à la mesure du segment \(AB\). Considérons les triangles \(ABC\) et \(ABD\). Ce sont des triangles équilatéraux (chacun de leurs côtés est, justement, un rayon des trois cercles congrus). Les angles intérieurs d’un triangle équilatéral sont tous de \(60^{\circ}\). En particulier, les angles \(BAC\) et \(ABD\) valent tous les deux \(60^{\circ}\). \[m\angle BAC = m\angle ABD = 60^{\circ}\]
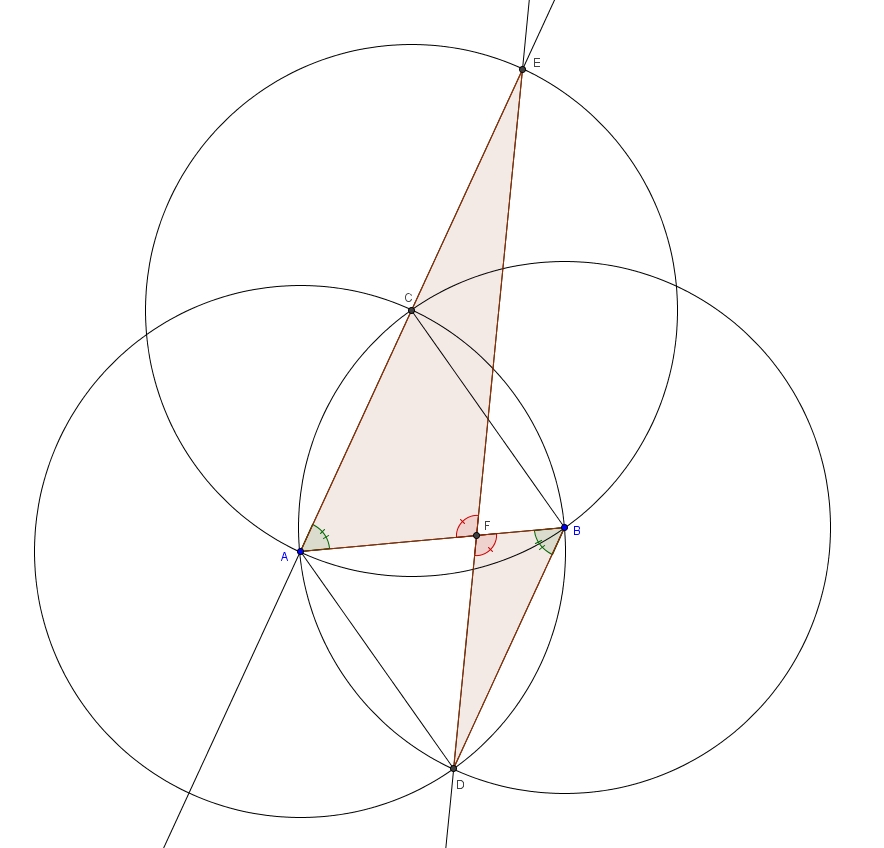
***Ici, Grasyop remarque qu’il existe une façon plus élégante d’établir la congruence des angles \(BAC\) et \(BAD\). On considère le losange \(ACBD\) (tous ses côtés ont pour mesure le rayon \(AB\)). Les côtés opposés d’un losange étant parallèles, on trouve que les angles \(BAC\) et \(ABD\) sont des angles alternes-internes isométriques. *** Les angles \(AFE\) et \(BFD\) sont eux aussi isométriques puisqu’ils sont opposés par le sommet. Les triangles \(AEF\) et \(BDF\) sont donc semblables par le cas de similitude AA.
Et comme dans des triangles semblables les côtés homologues sont dans le même rapport, on déduit ceci : la mesure de \(\overline{AE}\) étant égale à deux rayons et la mesure de \(\overline{BD}\) à un rayon, le rapport de similitude est \(2\). Et comme ce rapport est \(2\), cela implique que la mesure de \(\overline{AF}\) vaut deux fois celle de \(\overline{FB}\). Et si \(\overline{AF}\) est effectivement deux fois plus grand que \(\overline{FB}\), alors on trouve que la mesure de \(\overline{AB}\) est vaut trois fois celle de \(\overline{FB}\). C’est la trisection recherchée.
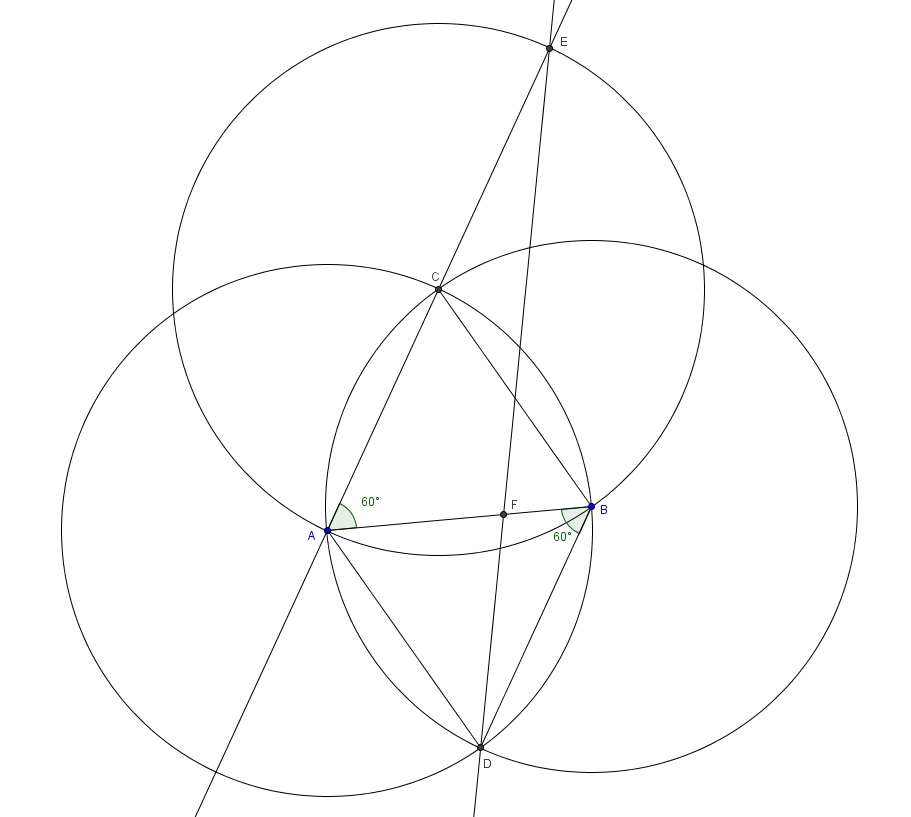
C’est Thalès : les parallèles (AE) et (BD) découpent sur les sécantes (AB) et (ED) des segments proportionnels.
Salut Graysop,
Thalès est bien en évidence en effet. Mais il faut d’abord montrer que les droites sont parallèles à partir de la construction (ce qui est fait avec les alternes-internes isométriques de 60°). Si tu as une autre façon, je suis bien à l’écoute !
Bonne journée !
Là où vous dites que ABC et ABD sont des triangles équilatéraux, on pourrait aussi bien dire à la place que ACBD est un losange (de côté 1 rayon), et que les côtés d’un losange sont parallèles.
C’est vrai que je n’apporte pas grand chose en nommant Thalès, qui n’est en fait qu’un cas particulier de triangles semblables. Et en plus, il paraît que le théorème n’est même pas dû à Thalès. Mais j’ai quand même trouvé éclairant le moment où j’ai reconnu Thalès sur cette figure, c’est pour ça que je l’ai écrit.
De même que j’ai trouvé éclairant le moment où j’ai reconnu F comme le centre de gravité du triangle AEE’ (E’ étant le symétrique de E par rapport à (AB)). Si l’on sait que le centre de gravité F est situé aux deux tiers de la médiane [AB]… Mais là, c’est sans doute moi qui prend un bazooka pour tuer une mouche.
Salut Grasyop !
C’est effectivement beaucoup plus élégant d’utiliser le losange.
Merci pour cet apport !
En espérant encore avoir réponse 5 ans après le dernier message…
La démonstration amène effectivement à l’évident, mais je pensais que la trisection d’un angle avait été considérée comme un problème impossible à résoudre à l’instar de la quadrature du cercle et de la duplication du cube.
Alors soit je n’ai pas bien compris ce qu’était la trisection d’un angle, soit ce n’est plus un problème insoluble ; en effet, il est facile de tracer une sécante aux deux demi-droites d’un angle de telle sorte que l’on forme un triangle équilatéral. De là, on obtient un segment dont la trisection est possible comme expliqué plus haut, puis il suffit de tracer les droites passant par l’angle et par les points nouvellement créés…
Qu’ais-je loupé? ^^’
Haaaaa… Fausse alerte, j’ai trouvé tout seul ce que j’ai loupé. La trisection du segment ne me donnera pas trois angles identiques. Il faudrait une trisection de segment courbe :-(