Suite à une discussion en classe, un élève est tombé, naviguant sur la toile, sur la Trompette de Gabriel. Comme il avait un peu de difficulté à saisir le concept, je lui ai proposé cet exemple d’une étonnante simplicité.
Traçons un rectangle de \(1 \times 1\). Au dessus du rectangle, traçons-en un deuxième de \(1 \times \frac{1}{2}\). Au dessus de ce dernier, au autre rectangle : celui là de \(1 \times \frac{1}{4}\). Et puis après, un autre rectangle de \(1 \times \frac{1}{8}\). Et ainsi de suite. On prétend continuer ce processus sans jamais s’arrêter (pour ce que cela peut bien vouloir dire).
On obtient une figure qui ressemble à celle-ci (justement baptisée gratte-ciel par l’élève en question), après \(8\) itérations
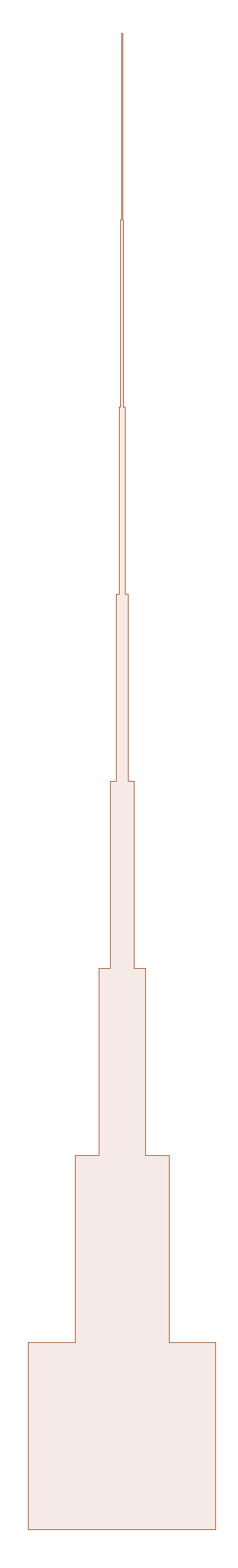 Pour ce qui est du périmètre, aucun doute, celui-là augmente de \(2\) unités à chaque itération. Le seul fait qu’on puisse ajouter deux à chaque itération est suffisant pour dire qu’on peut obtenir un périmètre aussi grand que l’on veut. Il suffit de continuer d’ajouter des étages au gratte-ciel. En d’autres mots, si le nombre d’itérations tend vers l’infini, le périmètre lui aussi tendra vers l’infini.
Pour ce qui est du périmètre, aucun doute, celui-là augmente de \(2\) unités à chaque itération. Le seul fait qu’on puisse ajouter deux à chaque itération est suffisant pour dire qu’on peut obtenir un périmètre aussi grand que l’on veut. Il suffit de continuer d’ajouter des étages au gratte-ciel. En d’autres mots, si le nombre d’itérations tend vers l’infini, le périmètre lui aussi tendra vers l’infini.
Qu’en est-il de l’aire ? L’aire du premier rectangle est égal à\[1 \times 1 = 1\]L’aire du deuxième\[1 \times \frac{1}{2} = \frac{1}{2}\]L’aire du troisième\[1 \times \frac{1}{4} = \frac{1}{4}\]et ainsi de suite. L’aire de la figure complète sera égale à la somme des aires des rectangles. Quelle est cette somme ? C’est nul autre que la somme des inverses des puissances de deux ! Et cette somme est bien connue ! C’est \(2\) ! \begin{align*}\text{Aire} &= 1 + \frac{1}{2} +\frac{1}{4} + \frac{1}{8}\ + \ \dots \\ \\ &= \sum_{k=0}^{\infty} \frac{1}{2^{k}}\\ \\ &=2 \end{align*}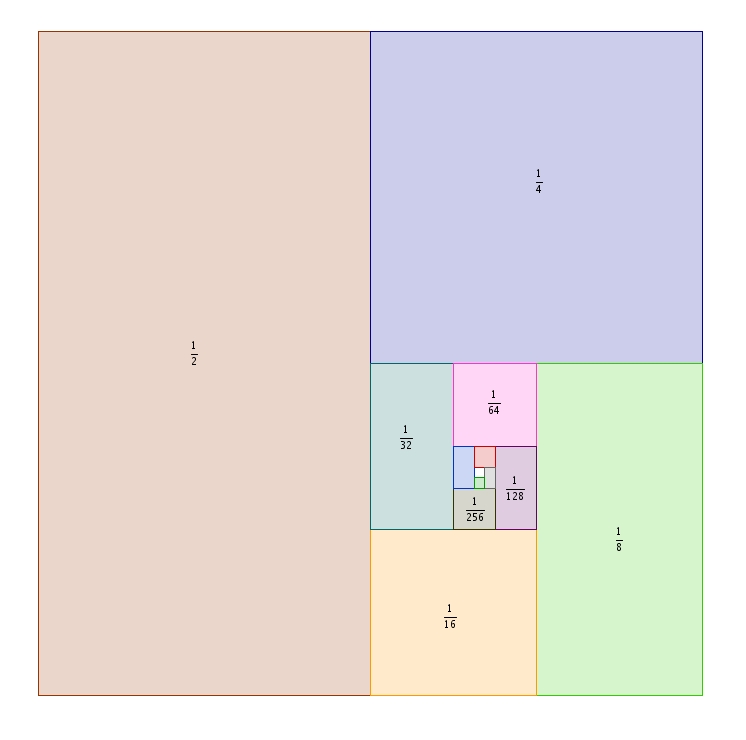 Le périmètre de ce gratte-ciel (infini) bien particulier est donc infini mais son aire, elle, est finie.
Le périmètre de ce gratte-ciel (infini) bien particulier est donc infini mais son aire, elle, est finie.
Bonjour,
le flocon de Koch est bien aussi, d’autant que son aire peut simplement être majorée par celle d’un même cercle, quel que soit le niveau d’itération. :)
Bonjour nonos,
tu as visé dans le mille puisque c’est justement en étudiant le flocon de Koch que nous en sommes venus à la trompette de Grabriel et au sujet du périmètre infini et aire finie. Le flocon fera l’objet d’un billet sous peu.
Merci de ton commentaire !