La trisectrice de Ceva

La trisection de l’angle est un problème classique de géométrie.  On sait aujourd’hui que la trisection ne peut être réalisée à la règle (non-marquée) et au compas.  Par contre, la trisection peut être réalisée avec d’autres instruments, quelques mécanismes produisant des courbes (que l’on appelle, vous l’aurez deviné, des courbes trisectrices !) Le mathématicien grec Nicomède (env. -280 – env. -210) en a découvert une, la conchoïde qui porte son nom, et qui permet de réaliser la trisection d’un angle.  La conchoïde de Nicomède est probablement la plus connue des courbes trisectrices.  En voici une autre…

La trisectrice de Ceva

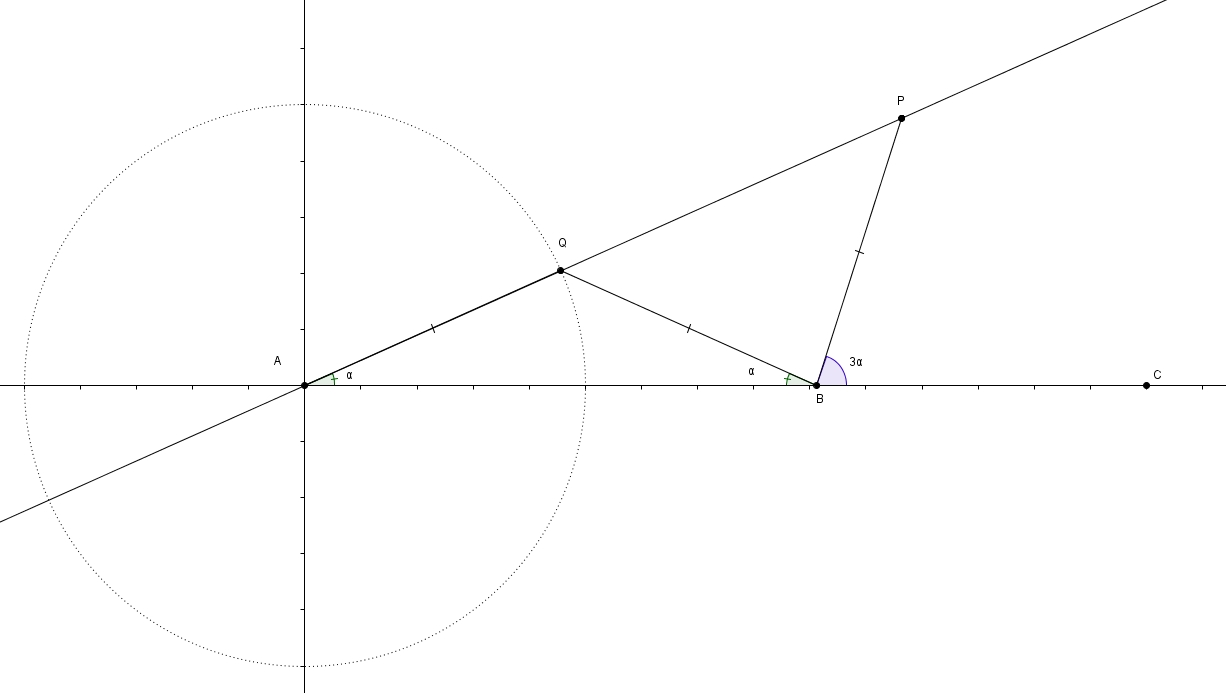
On construit la trisectrice de Ceva de telle manière.  On considère le cercle de centre $A$ et de rayon $\overline{AQ}$.  On considère aussi la droite $AC$.  La trisectrice est le lieu du point $P$, en déplaçant $Q$ sur le cercle, tels que $A$, $Q$ et $P$ soient colinéaires (alignés sur une même droite), que $B$ soit sur $AC$ et que $$m\overline{AQ}=m\overline{BQ}=m\overline{PQ}$$Voyons d’abord pourquoi cette courbe porte le nom de trisectrice.  Appelons $\alpha$ la mesure de l’angle $QAB$.  Comme le triangle $AQB$ est isocèle, la mesure de l’angle $ABQ$ est aussi $\alpha$ puisque les angles opposés aux côtés isométriques dans les triangles isocèles sont isométriques.  Comme la somme des angles intérieurs d’un triangle est toujours ${180}^{\circ }$, la mesure de l’angle $AQB$ est ${180}^{\circ }-2\alpha$.  La mesure de l’angle $PQB$ est de $2\alpha$ puisque ces deux angles sont adjacents supplémentaires.  Le triangle $QBP$ étant à son tour isocèle, on trouve que la mesure de l’angle $BPQ$ est donc elle aussi de $2\alpha$.  On trouve, dans le triangle $BPQ$, $$m\mathrm{\angle }PBQ+2\alpha +2\alpha ={180}^{\circ }$$Ce que l’on peut réécrire de la façon suivante $$m\mathrm{\angle }PBQ={180}^{\circ }-4\alpha$$Les angles $PBQ$, $ABQ$ et $PBC$ étant adjacents supplémentaires, on peut aussi écrire$$\alpha +m\mathrm{\angle }PBQ+m\mathrm{\angle }PBC={180}^{\circ }$$En substituant la mesure de l’angle $PBQ$ on obtient $$\alpha +{180}^{\circ }-4\alpha +m\mathrm{\angle }PBC={180}^{\circ }$$ce qui fait, bien entendu, $$m\mathrm{\angle }PBC=3\alpha$$

Les équations paramétriques

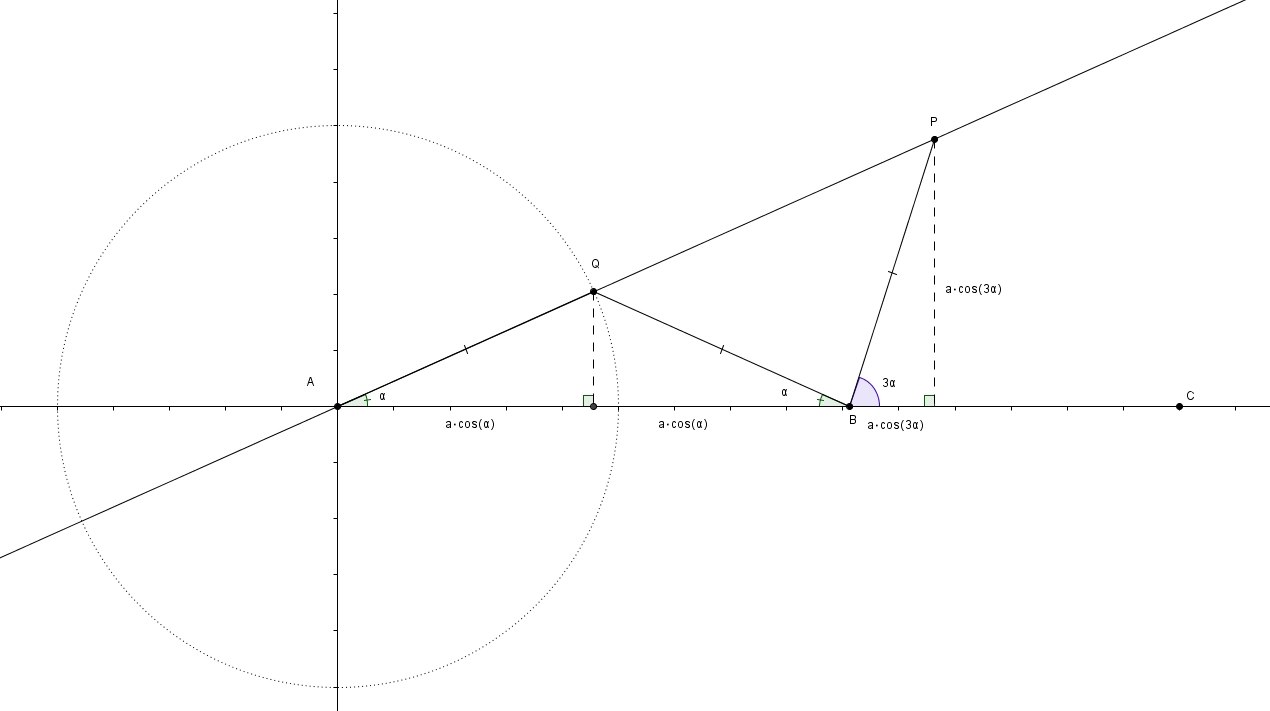
Trouvons maintenant les équations paramétriques de la courbe.  Plaçons $A$ à l’origine du plan cartésien.  Plaçons $C$ sur l’axe des abscisses.   Posons enfin $$m\overline{AQ}=a$$Les coordonnées de $Q$ sont $$(a\cos \left(\alpha \right),a\sin \left(\alpha \right))$$celles de $B$ sont$$(2\alpha \cos \left(\alpha \right),0)$$et donc celles de $P$ sont $$(2a\cos \left(\alpha \right)+a\cos \left(3\alpha \right),a\sin \left(3\alpha \right))$$

Mais sachant que $$\cos \left(3\alpha \right)=4{\cos }^3\left(\alpha \right)-3\cos \left(\alpha \right)$$On peut réécrire l’abscisse de $P$ $$x=2a\cos \left(\alpha \right)+a\cos \left(3\alpha \right)$$comme $$x=2a\cos \left(\alpha \right)+a(4{\cos }^3\left(\alpha \right)-3\cos \left(\alpha \right))$$ce qui fait d’abord $$x=2a\cos \left(\alpha \right)+4a{\cos }^3\left(\alpha \right)-3a\cos \left(\alpha \right)$$puis ensuite $$x=4a{\cos }^3\left(\alpha \right)-a\cos \left(\alpha \right)$$et enfin $$x=a(4{\cos }^3\left(\alpha \right)-\cos \left(\alpha \right))$$Sachant aussi que $$\sin \left(3\alpha \right)=3\sin \left(\alpha \right)-4{\sin }^3\left(\alpha \right)$$On peut réécrire l’ordonnée de $P$ $$y=a\sin \left(3\alpha \right)$$comme $$y=a(3\sin \left(\alpha \right)-4{\sin }^3\left(\alpha \right))$$En posant $$a=1$$on obtient les équations $$x=4{\cos }^3\left(\alpha \right)-\cos \left(\alpha \right),y=3\sin \left(\alpha \right)-4{\sin }^3\left(\alpha \right)$$dont voici la représentation graphique

Et avec les coordonnées polaires…

Pour les coordonnées polaires, elles peuvent prendre différentes formes.  En posant $$m\overline{AP}=r$$et en considérant le triangle rectangle d’hypoténuse $\overline{AP}$, on trouve l’une de ces formes avec $$\cos \left(\alpha \right)=\frac{a(4\cos \left(\alpha \right)-\cos \left(\alpha \right))}{r}$$(nul autre que le cosinus, rapport du côté opposé et de l’hypoténuse dans le triangle rectangle). Cela fait, en isolant $r$, $$r=\frac{a(4{\cos }^3\left(\alpha \right)-\cos \left(\alpha \right))}{\cos \left(\alpha \right)}$$et en simplifiant, $$r=a(4{\cos }^2\left(\alpha \right)-1)$$Voilà !