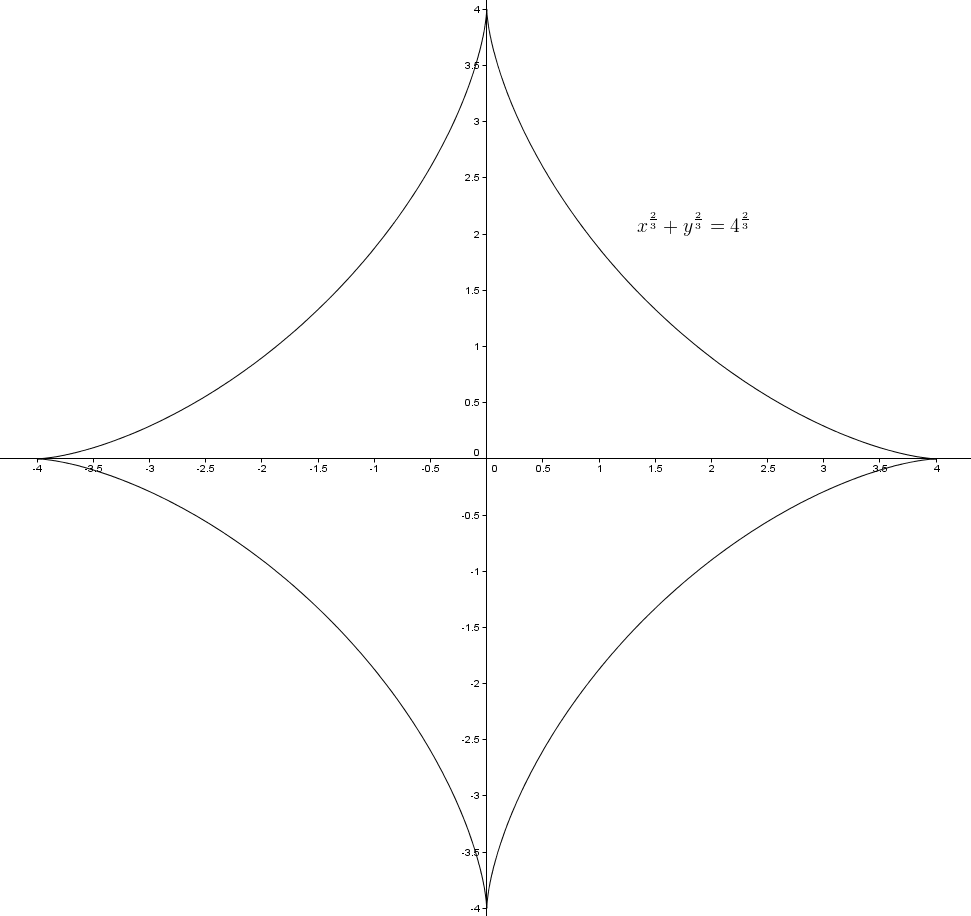
L’astroïde est la trace du point \(P\) d’un cercle de rayon \(\dfrac{R}{4}\) qui roule sans glisser à l’intérieur d’un cercle de rayon \(R\).
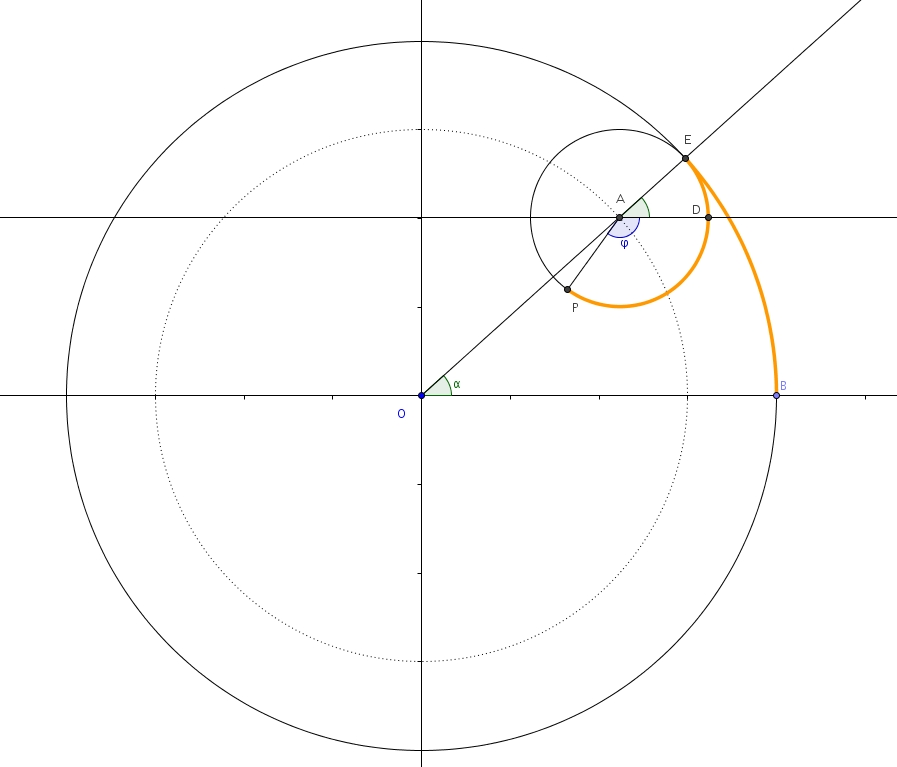
Sur la figure : le grand cercle rayon \(OB\), de centre \(O\), le petit cercle rayon \(AP\), de centre \(A\), avec \[m\overline{AP} = \frac{1}{4}m\overline{OB}\]qui roule sans glisser à l’intérieur du grand cercle. On considère la trace du point \(P\). On remarque que le centre \(A\) du petit cercle décriera une trajectoire telle qu’un cercle de rayon \[r = \frac{3}{4}m\overline{OB}\]et de centre \(O\) (en pointillé sur la figure). Le point \(E\) est le point de tangence entre les petit et grand cercles.
L’angle \(\alpha\) est l’angle que forme le centre \(A\) du petit cercle, le centre \(O\) du grand cercle et l’axe des abscisses (en vert sur la figure, l’angle \(AOB\), calculé dans le sens habituel, anti-horaire). En traçant la droite \(AD\) parallèle à l’axe, on obtient des angles correspondants isométriques. L’angle \(EAD\) a donc lui aussi pour mesure \(\alpha\). En posant \[\varphi = m\angle DAP\]calculé dans le sens horaire, on obtient \[m\angle EAP = \alpha + \varphi\]Enfin, avec \[m\overline{OB} = R\]on peut trouver les coordonnées du point \(A\) \[\left(\frac{3}{4}R\cos(\alpha), \ \frac{3}{4}R\sin(\alpha)\right)\]et celles de \(P\) \[\left(\frac{3}{4}R\cos(\alpha) + \frac{1}{4}\cos(\varphi), \ \frac{3}{4}R\sin(\alpha)-\frac{1}{4}R\sin(\varphi)\right)\]ou en effectuant la mise en évidence : \[\left(\frac{R}{4}\left(3\cos(\alpha)+\cos(\varphi)\right), \ \frac{R}{4}\left(3\sin(\alpha)-\sin(\varphi)\right)\right)\](Remarquez que, les angles étant orientés, \(\alpha\) dans le sens anti-horaire et \(\varphi\) dans le sens horaire, on additionne \(\frac{R}{4}\cos(\varphi)\) à l’abscisse et on soustrait \(\frac{R}{4}\sin(\varphi)\) à l’ordonnée.)
Comme le cercle roule sans glisser, on trouve aussi que les mesures des arcs \(EB\) et \(EDP\) sont égales. On a \[m\overset{\large\frown}{EDP} = \frac{R}{4}\left(\alpha + \varphi\right)\]et \[m\overset{\large\frown}{EB} = R\alpha\]Cela nous permet d’écrire \[\frac{R}{4}\left(\alpha + \varphi\right)= R\alpha\]ce qui fait \[\alpha + \varphi = 4\alpha\]et donc \[\varphi = 3\alpha\]Il nous est donc possible de réécrire l’expression pour les abscisses \[x = \frac{R}{4}\left(3\cos(\alpha)+\cos(\varphi)\right)\]et les ordonnées\[y=\frac{R}{4}\left(3\sin(\alpha)-\sin(\varphi)\right)\]du point point \(P\) de l’astroïde en fonction de l’angle \(\alpha\) seulement. On obtient \[x = \frac{R}{4}\left(3\cos(\alpha)+\cos(3\alpha)\right)\]et \[y = \frac{R}{4}\left(3\sin(\alpha)-\sin(3\alpha)\right)\]Or, comme \[\cos(3x)=4\cos^{3}(x)-3\cos(x)\]et \[\sin(3x)=3\sin(x)-4\sin^{3}(x)\]on peut substituer les expressions \(\cos(3\alpha)\) et \(\sin(3\alpha)\) dans les équations précédentes. On obtient pour les abscisses \[x = \frac{R}{4}\left(3\cos(\alpha)+4\cos^{3}(\alpha)-3\cos(\alpha)\right)\]ce qui se simplifie d’abord à\[x = \frac{R}{4}\left(4\cos^{3}(\alpha)\right)\]puis à\[x = R\cos^{3}(\alpha)\]On obtient pour les ordonnées \[y = \frac{R}{4}\left(3\sin(\alpha)-\left(3\sin(\alpha)-4\sin^{3}(\alpha)\right)\right)\]ce qui fait d’abord\[y = \frac{R}{4}\left(3\sin(\alpha)-3\sin(\alpha)+4\sin^{4}(\alpha)\right)\]puis \[y = \frac{R}{4}\left(4\sin^{3}(\alpha)\right)\]et enfin tout simplement \[y = R\sin^{3}(\alpha)\]Les équations \[x=R\cos^{3}(\alpha)\]et \[y = R\sin^{3}(\alpha)\]sont les équations paramétriques de l’astroïde. On peut trouver la forme cartésienne générale comme suit. Dans l’équation des abscisses, on divise les deux côtés par \(R\) \[\frac{x}{R} = \cos^{3}(\alpha)\]puis on prend la racine cubique \[\sqrt[3]{\frac{x}{R}} = \cos(\alpha)\]que l’on peut aussi écrire \[\frac{x^{\frac{1}{3}}}{R^{\frac{1}{3}}}=\cos(\alpha)\]On élève au carré \[\left(\frac{x^{\frac{1}{3}}}{R^{\frac{1}{3}}}\right)^{2} = \cos^{2}(\alpha)\]ce qui fait\[\frac{x^{\frac{2}{3}}}{R^{\frac{2}{3}}}=\cos^{2}(\alpha)\]On procède ensuite avec les ordonnées, en divisant par \(R\) \[\frac{y}{R} = \sin^{3}(\alpha)\]puis en prenant la racine cubique \[\sqrt[3]{\frac{y}{R}}=\sin(\alpha)\]ce qui fait \[\frac{y^{\frac{1}{3}}}{R^{\frac{1}{3}}}=\sin(\alpha)\]On élève au carré \[\left(\frac{y^{\frac{1}{3}}}{R^{\frac{1}{3}}}\right)^{2}=\sin^{2}(\alpha)\]que l’on peut aussi réécrire comme\[\frac{y^{\frac{2}{3}}}{R^{\frac{2}{3}}} = \sin^{2}(\alpha)\]Il suffit enfin de ressortir notre bonne vieille identité trigonométrique \[\cos^{2}(\alpha)+\sin^{2}(\alpha)=1\]et de judicieusement remplacer \(\cos^{2}(\alpha)\) et \(\sin^{2}(\alpha)\) et obtenir \[\frac{x^{\frac{2}{3}}}{R^{\frac{2}{3}}}+\frac{y^{\frac{2}{3}}}{R^{\frac{2}{3}}}=1\]En multipliant chaque terme par \(R^{\frac{2}{3}}\), on obtient l’équation cartésienne générale \[x^{\frac{2}{3}}+y^{\frac{2}{3}}=R^{\frac{2}{3}}\]dont voici la représentation graphique