Je partage cette petite trouvaille rencontrée en élaborant un exercice pour mes élèves sur la droite d’Euler : il s’agit d’un triangle scalène, non rectangle, dans lequel les trois sommets (A, B, C), les trois pieds des hauteurs (H1, H2, H3), les trois points milieux des côtés (M1, M2, M3) et les points d’intersection des médianes (M0), médiatrices (R0) et hauteurs (H0) ont tous des coordonnées entières et dont les côtés ne sont pas parallèles aux axes. Qui plus est, les pieds des hauteurs tombent sur les côtés (et non sur leurs prolongements) et les trois points d’intersection se trouvent à l’intérieur du triangle.
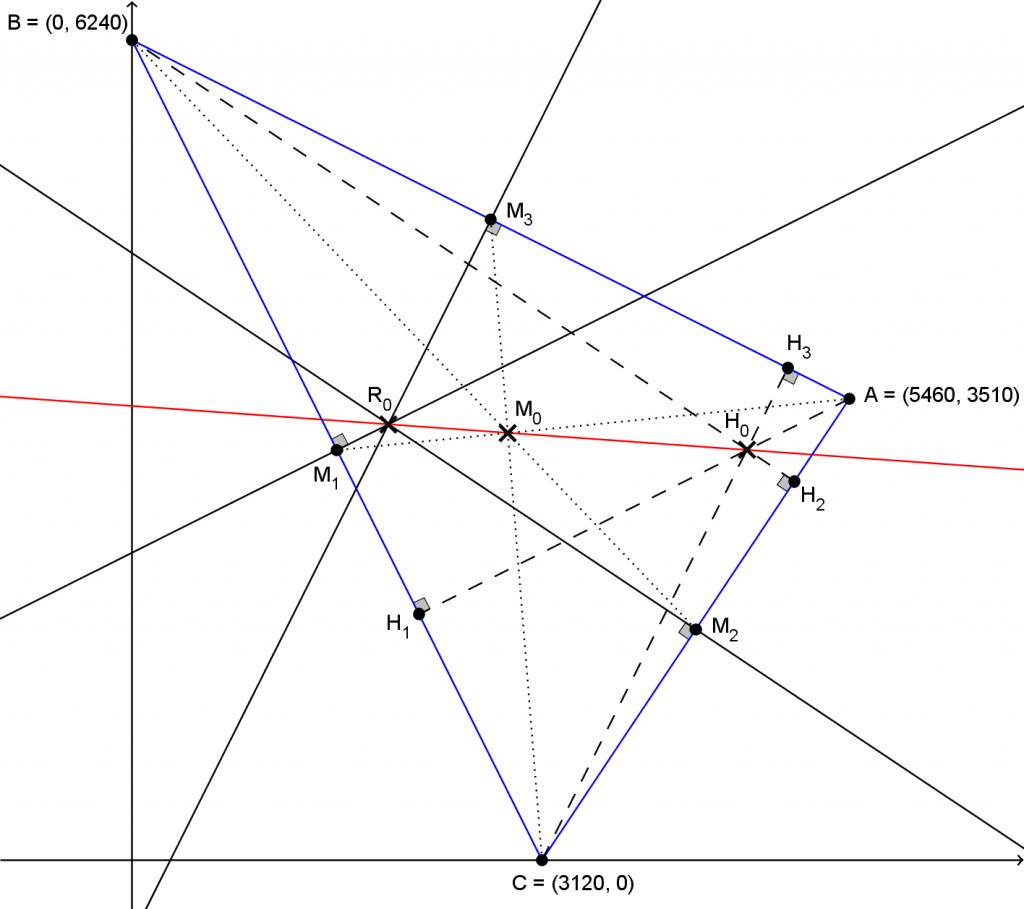Sur la figure, le triangle, en bleu, les médianes tracées avec des traits pointillés fins, les hauteurs avec des traits pointillés longs, et les médiatrices avec des traits continus. La droite d’Euler est en rouge.
Si on laisse tomber la condition que les points d’intersections H0, R0 et M0 soient à l’intérieur du triangle, on peut trouver facilement des triangles beaucoup plus petits (il en existe beaucoup), par exemple celui-ci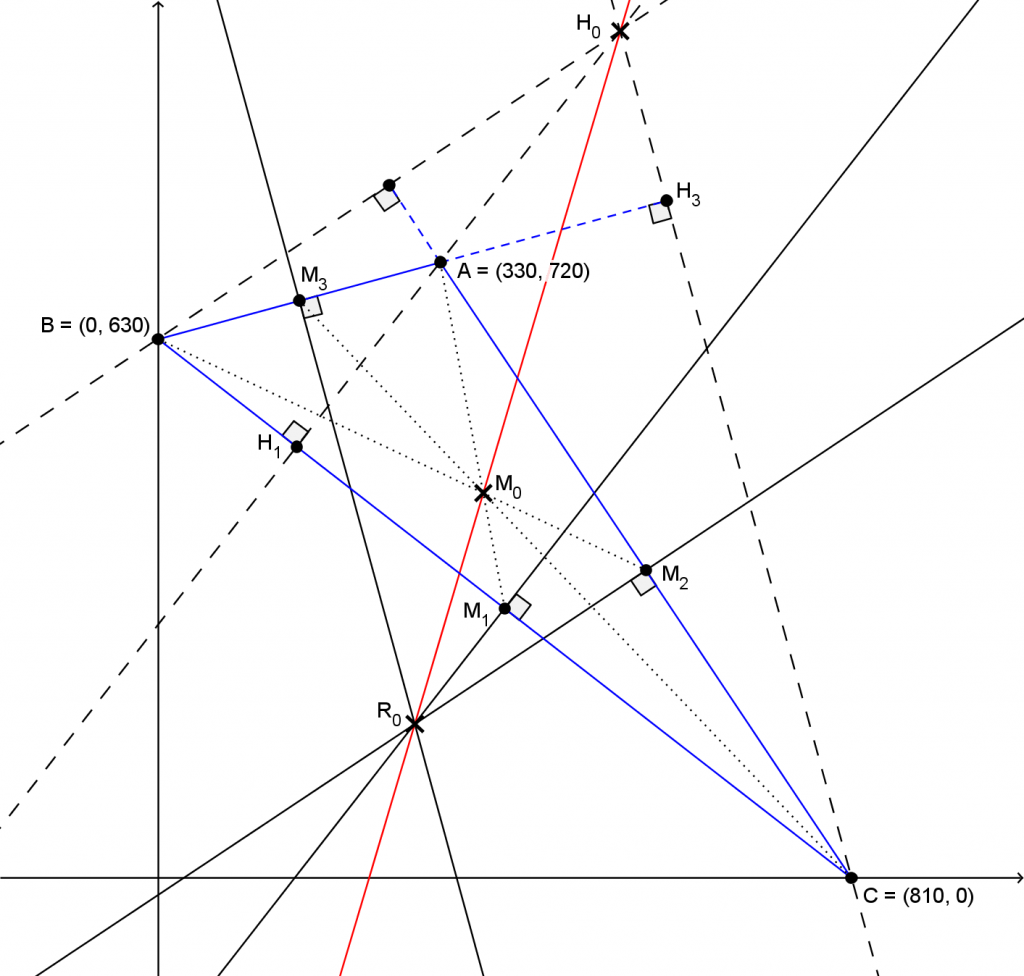
Bon. Je suis loin d’avoir fait une recherche exhaustive, mais voilà : je doute qu’il existe des triangles beaucoup plus petits que celui ci-dessus. Si vous en trouvez, s’il vous plait, faites-moi en part !
En ce qui me concerne, après tâtonnements dans Géogébra, j’ai cru bon partir du point d’intersection des médiatrices, équidistant des trois sommets, et de reconstruire les sommets du triangle à partir de là. Pour éviter d’obtenir des triangles rectangles (R0 tombe sur l’hypoténuse) ou isocèles, ou des côtés parallèles aux axes, j’ai utilisé pour les accroissements le plus petit nombre exprimable comme somme de deux carrés de trois façons différentes : \[325 = 1^{2}+18^{2}=66^{2}+17^{2}=10^{2}+15^{2}\]Après un peu de jonglerie avec les combinaisons possibles de ces nombres, j’ai ensuite redimensionné le triangle afin que tous les points mentionnés ci-haut soient à coordonnées entières (en multipliant les accroissements par le PPCM des dénominateurs des coordonnées rationnelles). Je n’ai aucune idée cependant si cette démarche est la meilleure !