Multiplication de logarithmes

Chers lecteurs aguerris,

Vous pouvez passer au point 4 immédiatement. Les premiers points sont là sur ce blogue pour fin de complétude.

4. Le produit de logarithmes

Le résultat qui suit provient de la solution (erronée) mais néanmoins amusante au problème :

Que vaut l’expression suivante (sans tables et sans calculatrice):

\[\log_{13}\left(243\right)\log_{3}\left(169\right)\]

En posant\[a=\log_{13}\left(243\right),\quad b = \log_{3}\left(169\right)\]on peut passer à la forme exponentielle équivalente \[13^{a} = 243, \quad 3^{b} = 169\]soustraire respectivement \(243\) et \(169\) de chaque côté et faire la somme des deux équations \[13^{a}-243 = 0, \quad 3^{b}-169 = 0\] \[13^{a}-243 + 3^{b}-169 = 0\]On peut réarranger les termes\[13^{a}-169 + 3^{b}-243=0\]et là, certainement, on trouve les solutions « évidentes » \[a = 2, \quad b = 5\]c’est-à-dire qu’on peut répondre à la question \begin{align*}\log_{13}\left(243\right) \log_{3}\left(169\right)&= ab\\ \\ &=2\cdot 5 \\ \\ &=10\end{align*}La réponse au problème, \(10\), est bonne, mais la démarche est fausse : il est évident que \(a\) et \(b\) ne peuvent prendre respectivement les valeurs \(2\) et \(5\) car \[2 \neq \log_{13}\left(243\right)\]et \[5\neq \log_{3}\left(169\right)\]Pourtant le produit est bien \(10\) ! Hasard ? Oh!  Je ne pense pas.

On considère le produit \[\log_{c}\left(x\right)\log_{d}\left(y\right)\]Avec la loi du changement de bases (voir point 3), \[\log_{c}\left(x\right)\log_{d}\left(y\right) = \frac{\log_{d}\left(x\right)}{\log_{d}\left(c\right)} \cdot \frac{\log_{c}\left(y\right)}{\log_{c}\left(d\right)}\]et quelques manipulations algébriques\begin{align*}\frac{\log_{d}\left(x\right)}{\log_{d}\left(c\right)} \cdot \frac{\log_{c}\left(y\right)}{\log_{c}\left(d\right)} &= \log_{d}\left(x\right)\log_{c}\left(y\right) \cdot \frac{1}{\log_{d}\left(c\right)\log_{c}\left(d\right)} \\ \\ &=\log_{d}\left(x\right)\log_{c}\left(y\right) \cdot \frac{1}{\log_{d}\left(c\right)\frac{\log_{d}\left(d\right)}{\log_{d}\left(c\right)}} \\ \\ &= \log_{d}\left(x\right)\log_{c}\left(y\right) \cdot \frac{1}{\log_{d}\left(c\right)\frac{1}{\log_{d}\left(c\right)}} \\ \\ &=\log_{d}\left(x\right)\log_{c}\left(y\right) \cdot \frac{1}{1} \\ \\ &= \log_{d}\left(x\right) \log_{c}\left(y\right) \end{align*}on trouve la jolie égalité suivante \[\log_{c}\left(x\right)\log_{d}\left(y\right) = \log_{d}\left(x\right)\log_{c}\left(y\right)\]Ainsi, on a effectivement \begin{align*}\log_{13}\left(243\right)\log_{3}\left(169\right) &= \log_{3}\left(243\right)\log_{13}\left(169\right) \\ \\ &= 5 \cdot 2 \\ \\ &= 10\end{align*}Dans son livre, Edward J. Barbeau [1] fait remarquer que la courbe strictement décroissante et concave d’équation \[13^{x} + 3^{y} = 412\] intercepte l’hyperbole équilatère d’équation\[xy=10\]en deux endroits : \(\left(2, \ 5\right)\) et \(\big(\log_{13}\left(243\right), \ \log_{3}\left(169\right)\big) \).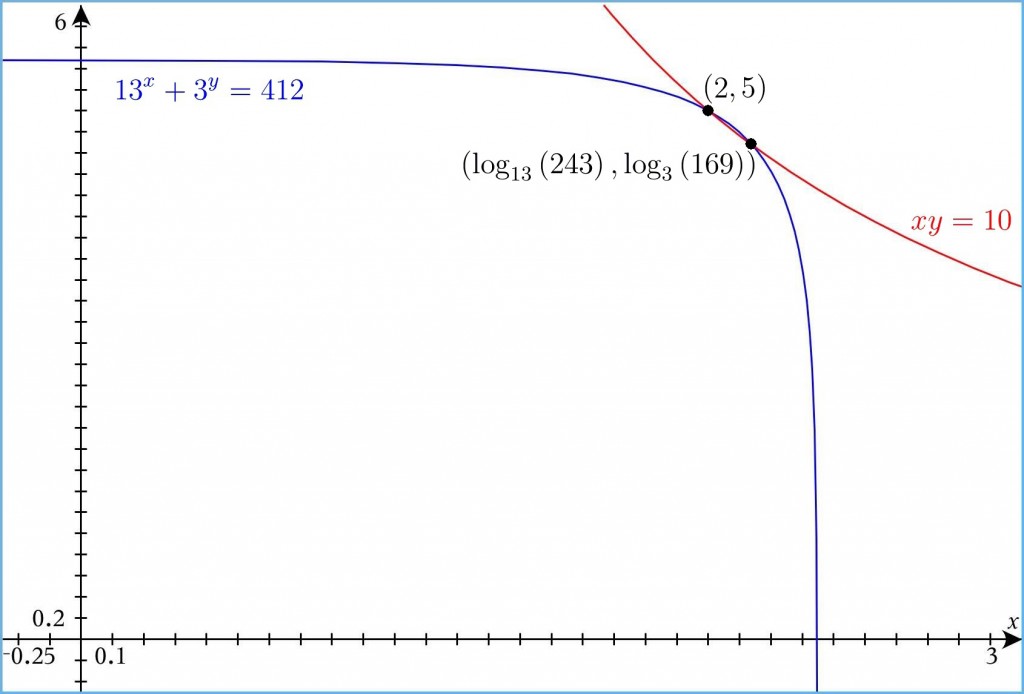

Merci TI Nspire CAS pour le joli implicitplot.

1. Le logarithme d’un produit

En partant de la définition,\[c^{\log_{c}\left(x\right)}=x\]on considère, d’une part, le produit \(xy\)\[x \cdot y = c^{\log_c\left(x\right)} \cdot c^{\log_{c}\left(y\right)}\]Avec un produit de deux puissances de même base, on additionne les exposants. \[x \cdot y = c^{\log_{c}\left(x\right) + \log_c\left(y\right)}\]D’autre part, toujours en partant de la définition du logarithme, on considère \[x \cdot y = c^{\log_{c}\left(x \cdot y\right)}\]Ainsi, on trouve\[c^{\log_{c}\left(x\cdot y\right)} = c^{\log_{c}\left(x\right)+\log_{c}\left(y\right)}\]et comme les bases sont égales, les exposants sont égaux ! On a donc \[\log_{c}\left(x \cdot y\right) = \log_{c}\left(x\right) + \log_{c}\left(y\right)\]On procède de la même manière pour le logarithme d’un quotient. On obtient dans ce cas-ci \[\log_{c}\left(\frac{x}{y}\right) = \log_{c}\left(x\right)-\log_{c}\left(y\right)\]

2. Le logarithme d’une puissance

En partant de la définition, on considère, d’une part, la puissance \[a^{x} = \left(c^{\log_{c}\left(a\right)}\right)^{x}\]Avec une puissance elle-même affectée d’un exposant, on multiplie les exposants\[a^{x}= c^{x\cdot \log_{c}\left(a\right)}\]D’autre part, toujours en partant de la définition du logarithme, on considère \[a^{x} = c^{\log_{c}\left(a^{x}\right)}\]Ainsi, on trouve \[c^{\log_{c}\left(a^{x}\right)} = c^{x\cdot \log_{c}\left(a\right)}\]et comme les bases sont égales, les exposants sont égaux ! On a donc \[\log_{c}\left(a^{x}\right) = x \cdot \log_{c}\left(a\right)\]

3. La loi du changement de bases

En partant de la définition, on considère les expressions suivantes \[c^{\log_{c}\left(x\right)}=x\]et \[d^{\log_{d}\left(x\right)} = x\]On substitut \(x\), dans la deuxième expression, à gauche, par l’expression qui lui est égale dans la première. \[d^{\log_{d}\left(c^{\log_{c}\left(x\right)}\right)}=x\]
En utilisant le résultat sur le logarithme d’une puissance, on réécrit l’expression précédente comme\[d^{\log_{c}\left(x\right)\cdot\log_{d}\left(c\right)} = x\]Mais comme on avait aussi précédemment\[d^{\log_{d}\left(x\right)} = x\]on trouve \[d^{\log_{c}\left(x\right)\cdot \log_{d}\left(c\right)} = d^{\log_{d}\left(x\right)}\]
et comme les bases sont égales, les exposants sont égaux ! \[\log_{c}\left(x\right) \cdot \log_{d}\left(c\right) = \log_{d}\left(x\right)\]En divisant chaque côté par \(\log_{d}\left(c\right)\), on obtient \[\log_{c}\left(x\right) = \frac{\log_{d}\left(x\right)}{\log_{d}\left(c\right)}\]On note qu’en divisant, si \(c \neq 1\), alors \(\log_{d}\left(c\right) \neq 0\).

Références : [1] Barbeau,Edward J.  (2000), Mathematical Fallacies, Flaws, and Flimflam

Freiling, Chris, The Change of Base Formula for Logarithms, College Mathematics Journal 17 (1986), p413