L’aire d’un octogone régulier… en deuxième secondaire

Il faut parfois faire attention de ne pas sauter trop rapidement aux conclusions. Trop habitués aux exercices prévisibles des manuels et cahiers, il peut parfois être déroutant de tomber sur quelque chose de rafraîchissant (au fait, ça en dit long sur les exercices qu’on présente aux élèves).

À l’aide aux devoirs la semaine passée :

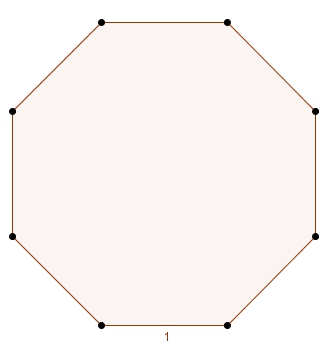
Trouver l’aire d’un octogone régulier de côté \(1\).

Le hic, c’est que la question est posée en deuxième secondaire. La réponse d’un de mes collègues (et la mienne de prime abord, je dois l’avouer) : hummm, il doit y avoir une erreur… c’est un problème de quatrième secondaire, tu as besoin de la trigonométrie (tangente) pour y arriver. En plus, tu n’as pas vu la relation de Pythagore… impossible à faire !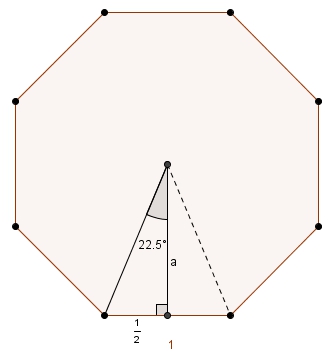

En effet, en utilisant la tangente pour trouver la mesure de l’apothème, c’est facile. Comment faire autrement, avec pour seuls concepts ceux vus en deuxième secondaire ? Ah ! Mais en utilisant un peu de symétrie, on peut se concentrer sur le quart de la figure.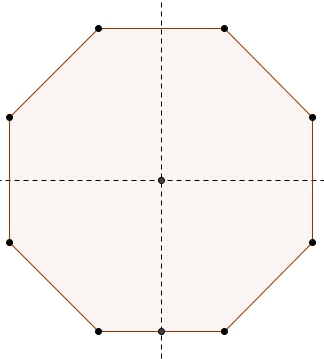
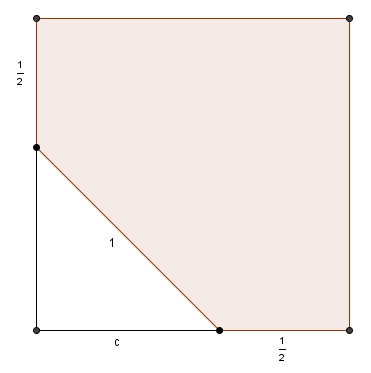On peut compléter la figure pour obtenir un carré. Il suffirait de soustraire l’aire du triangle rectangle blanc au grand carré. Les angles intérieurs et extérieurs sont au programme du premier cycle. L’angle extérieur d’un octogone régulier étant \(45^{\circ}\), ce triangle blanc est un triangle rectangle isocèle (on aurait pu aussi réfléchir davantage à la symétrie de la figure au lieu de passer par les angles extérieurs).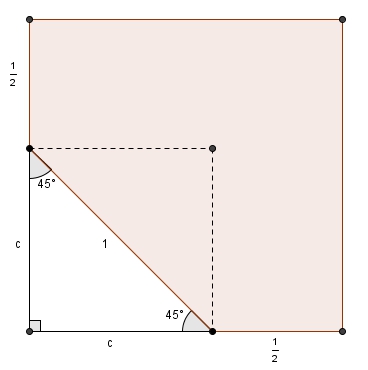

Comment trouver les dimensions du triangle (sans Pythagore) ? On construit un carré en effectuant la réflexion du triangle. Le carré étant un losange, et l’aire des figures étant au programme de deuxième secondaire, on calcule l’aire du carré avec ses diagonales : \[A_{\text{carré}} = \frac{1\times 1}{2} = \frac{1}{2}\]et la mesure du son côté \begin{align*}c^{2}&= \frac{1}{2} \\ \\ \\ c &= \sqrt{\frac{1}{2}} \\ \\ &= \frac{\sqrt{2}}{2}\end{align*}(en deuxième secondaire on utilise la calculatrice ici et on termine avec des valeurs approximatives.) L’aire du grand carré est donc : \[\left(\frac{1+\sqrt{2}}{2}\right)^{2} = \frac{3+2\sqrt{2}}{4}\]On soustrait l’aire du triangle (la moitié de l’aire du carré, c’est-à-dire \(\frac{1}{4}\)) \begin{align*}\frac{3+2\sqrt{2}}{4}-\frac{1}{4} &= \frac{2+2\sqrt{2}}{4} \\ \\ &= \frac{1 + \sqrt{2}}{2}\end{align*}et on multiplie par \(4\) pour obtenir l’aire de l’octogone complet \[\frac{1+\sqrt{2}}{2} \times 4 = 2 + 2\sqrt{2}\]Et voilà !