Cette histoire commence candidement par la recherche d’une expression équivalente pour \(\tan\!\left(\!\frac{1}{2}\theta\right)\), ce qui est tout à fait légitime car on connaît déjà des formules semblables pour le sinus et le cosinus, et se terminera par la résolution d’équations quadratiques avec des méthodes trigonométriques, méthodes inusuelles tombées en désuétude en même temps que les tables et les règles à calculer.
La tangente du demi-angle
En partant des formules pour l’addition des angles, on peut redécouvrir les expressions analogues pour le sinus et le cosinus. On sait que \[\sin(\alpha + \beta) = \sin(\alpha)\cos(\beta) + \sin(\beta)\cos(\alpha)\]d’où on tire \begin{align*}\sin(2 \alpha) &= \sin(\alpha + \alpha) \\ \\ &=\sin(\alpha)\cos(\alpha) + \sin(\alpha)\cos(\alpha) \\ \\ &= 2\sin(\alpha)\cos(\alpha)\end{align*}En posant \(\alpha = \frac{1}{2}\theta\), on obtient \[\sin(2\alpha) = 2\sin(\alpha)\cos(\alpha)\] \[\sin(\theta) = 2\sin\!\left(\frac{1}{2}\theta\right)\cos\!\left(\frac{1}{2}\theta\right)\]ce qui nous permet de tirer \[\sin\!\left(\frac{1}{2}\theta\right) = \frac{\sin(\theta)}{2\cos\!\left(\frac{1}{2}\theta\right)}\]Une démarche semblable pour le cosinus utilisant la formule \[\cos(\alpha + \beta) = \cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)\]nous donne \begin{align*}\cos(2\alpha) &= \cos(\alpha + \alpha) \\ \\ &=\cos(\alpha)\cos(\alpha)-\sin(\alpha)\sin(\alpha) \\ \\ &= \cos^{2}(\alpha)-\sin^{2}(\alpha) \\ \\ &= \cos^{2}(\alpha)-\left(1-\cos^{2}(\alpha)\right) \\ \\ &=2\cos^{2}(\alpha)-1\end{align*}Après la même substitution \(\alpha = \frac{1}{2}\theta\), on a \[\cos\left(2\alpha\right) = 2\cos^{2}\left(\alpha\right) -1\] \[\cos(\theta) = 2\cos^{2}\!\left(\frac{1}{2}\theta\right)-1\]ou, en isolant \(\cos^{2}\!\left(\frac{1}{2}\theta\right)\), \[\cos^{2}\!\left(\frac{1}{2}\theta\right) = \frac{\cos(\theta)+1}{2}\]On a maintenant tous les ingrédients pour trouver une expression pour \(\tan\!\left(\frac{\theta}{2}\right)\).\begin{align*}\tan\!\left(\frac{1}{2}\theta\right) &= \frac{\sin\!\left(\frac{1}{2}\theta\right)}{\cos\!\left(\frac{1}{2}\theta\right)} \\ \\ &= \frac{\frac{\sin(\theta)}{2\cos\left(\frac{1}{2}\theta\right)}}{\cos\!\left(\frac{1}{2}\theta\right)} \\ \\ &= \frac{\sin\left(\theta\right)}{2\cos^{2}\!\left(\frac{1}{2}\theta\right)} \\ \\ &= \frac{\sin\left(\theta\right)}{2\left(\frac{\cos\left(\theta\right)+1}{2}\right)}\\ \\ &= \frac{\sin\left(\theta\right)}{\cos\left(\theta\right) + 1}\end{align*}Joli non ? Déjà armé de notre expression pour \(\cos^{2}\!\left(\frac{1}{2}\theta\right)\), on pourrait être tenté par une expression pour \(\tan^{2}\!\left(\frac{1}{2}\theta\right)\). Après tout, pourquoi pas ? \begin{align*}\tan^{2}\!\left(\frac{1}{2}\theta\right)&=\left(\frac{\sin(\theta)}{\cos(\theta) + 1}\right)^{2} \\ \\ &=\frac{\sin^{2}(\theta)}{\left(\cos(\theta ) + 1\right)^{2}} \\ \\ &=\frac{1-\cos^{2}(\theta)}{\left(\cos(\theta) + 1\right)^{2}} \\ \\ &=\frac{(1-\cos(\theta))(1+\cos(\theta))}{\left(\cos(\theta) + 1\right)^{2}} \\ \\ &= \frac{1-\cos(\theta)}{\cos(\theta) + 1}\end{align*}Ah ! On a le même dénominateur \(\cos(\theta) + 1\) dans les deux expressions, celle pour \(\tan\!\left(\frac{1}{2}\theta\right)\) et celle pour \(\tan^{2}\!\left(\frac{1}{2}\theta\right)\). Il est possible d’exprimer l’une en fonction de l’autre. \begin{align*}\tan^{2}\!\left(\frac{1}{2}\theta\right) &= \frac{1-\cos(\theta)}{\cos(\theta)+1} \\ \\ &= \frac{-2\cos(\theta) + \cos(\theta) + 1}{\cos(\theta) + 1} \\ \\ &= \frac{-2\cos(\theta)}{\cos(\theta) + 1} + \frac{\cos(\theta) + 1}{\cos(\theta) + 1} \\ \\ &= \frac{-2\cos(\theta)}{\cos(\theta) + 1} + 1 \\ \\ &= \frac{-2\cos(\theta)\cdot \sin(\theta)}{\left(\cos(\theta) + 1\right) \cdot \sin(\theta)} + 1 \\ \\ &=\frac{-2\cos(\theta)}{\sin(\theta)} \cdot \frac{\sin(\theta)}{\cos(\theta) + 1} + 1 \\ \\ &= -2\cot(\theta)\cdot \tan\!\left(\frac{1}{2}\theta\right) + 1 \\ \\ &= \frac{-2}{\tan(\theta)}\cdot \tan\!\left(\frac{1}{2}\theta\right) + 1\end{align*}On peut réécrire la dernière ligne comme \[\tan^{2}\!\left(\frac{1}{2}\theta\right) + \frac{2}{\tan\left(\theta\right)}\cdot \tan\!\left(\frac{1}{2}\theta\right)-1 = 0\]ce qui ressemble drôlement à une équation du deuxième degré en \(\tan\!\left(\frac{1}{2}\theta\right)\). Ce n’est pas la seule équation de la sorte qui soit possible d’obtenir. On aurait pu aussi faire quelque chose comme \begin{align*}\tan^{2}\!\left(\frac{1}{2}\theta\right) &= \frac{1-\cos\left(\theta\right)}{\cos\left(\theta\right) + 1} \\ \\ &= \frac{2-\cos(\theta)-1}{\cos(\theta+1)}\\ \\ &=\frac{2-\left(\cos(\theta) + 1\right)}{\cos(\theta) + 1} \\ \\ &= \frac{2}{\cos(\theta) + 1}-\frac{\cos(\theta) + 1}{\cos(\theta) + 1} \\ \\ &= \frac{2}{\cos(\theta) + 1}-1\\ \\ &= \frac{2\cdot \sin(\theta)}{\left(\cos(\theta) + 1\right) \cdot \sin(\theta)}-1 \\ \\ &= \frac{2}{\sin(\theta)} \cdot \frac{\sin(\theta)}{\cos(\theta)+1}-1 \\ \\ &= \frac{2}{\sin(\theta)}\cdot \tan\!\left(\frac{1}{2}\theta\right)-1\end{align*}À l’instar de ce qu’on a fait plus tôt, on réécrit \[\tan^{2}\!\left(\frac{1}{2}\theta\right)-\frac{2}{\sin(\theta)}\cdot \tan\!\left(\frac{1}{2}\theta\right)+1=0\]
Sans autre explication ou motivation, mes choix pour exprimer \(\tan^{2}\!\left(\frac{1}{2}\theta\right)\) en fonction de \(\tan\!\left(\frac{1}{2}\theta\right)\) sont discutables. Après tout, il aurait été beaucoup plus simple d’écrire \begin{align*}\tan^{2}\!\left(\frac{1}{2}\theta\right)&= \frac{1-\cos(\theta)}{\cos(\theta)+1} \\ \\ &= \frac{\sin(\theta)}{\sin(\theta)} \cdot \frac{1-\cos(\theta)}{\cos(\theta) + 1} \\ \\ &= \frac{1-\cos(\theta)}{\sin(\theta)}\cdot \frac{\sin(\theta)}{\cos(\theta)+1} \\ \\ &= \frac{1-\cos(\theta)}{\sin(\theta)}\cdot \tan\!\left(\frac{1}{2}\theta\right)\end{align*}Or, la démarche qui nous a permis d’obtenir des expressions quI s’apparentent à des trinômes du deuxième degré n’est définitivement pas le fruit du hasard. Ces équations nous permettent de résoudre… des équations du deuxième degré !
Résolution d’équations quadratiques
Armé de nos deux équations \[\tan^{2}\!\left(\frac{1}{2}\theta\right) + \frac{2}{\tan\left(\theta\right)}\cdot \tan\!\left(\frac{1}{2}\theta\right)-1 = 0\] \[\tan^{2}\!\left(\frac{1}{2}\theta\right)-\frac{2}{\sin(\theta)}\cdot \tan\!\left(\frac{1}{2}\theta\right)+1=0\]on peut s’attaquer à la résolution d’équations quadratiques. Il y a clairement une ressemblance entre l’équation\[x^2 + bx + c = 0\] et les équations \[\tan^{2}\!\left(\frac{1}{2}\theta\right) + \frac{2}{\tan\left(\theta\right)}\cdot \tan\!\left(\frac{1}{2}\theta\right)-1 = 0\]ou \[\tan^{2}\!\left(\frac{1}{2}\theta\right)-\frac{2}{\sin(\theta)}\cdot \tan\!\left(\frac{1}{2}\theta\right)+1=0\]
Laquelle des équations en \(\tan\!\left(\frac{1}{2}\theta\right)\) on choisit déprend du signe de \(c\). Si \(c<0\), on utilise \[\tan^{2}\!\left(\frac{1}{2}\theta\right) + \frac{2}{\tan\left(\theta\right)}\cdot \tan\!\left(\frac{1}{2}\theta\right)-1 = 0\]alors que si \(c>0\), on utilise \[\tan^{2}\!\left(\frac{1}{2}\theta\right)-\frac{2}{\sin(\theta)}\cdot \tan\!\left(\frac{1}{2}\theta\right)+1=0\]Bon ça va pour le signe, mais une astuce supplémentaire s’impose. On a noté la ressemblance, mais les équations \[x^2 + bx + c = 0\] et \[\tan^{2}\!\left(\frac{1}{2}\theta\right) + \frac{2}{\tan\left(\theta\right)}\cdot \tan\!\left(\frac{1}{2}\theta\right)-1 = 0\]ou \[\tan^{2}\!\left(\frac{1}{2}\theta\right)-\frac{2}{\sin(\theta)}\cdot \tan\!\left(\frac{1}{2}\theta\right)+1=0\] ne sont pas en tout point identiques. Dans les équations trigonométriques, le terme constant est \(1\), pas \(c\). Si on ne fait que diviser \[x^2 + bx + c = 0\]par \(c\), le coefficient de \(x^2\) ne sera plus \(1\) mais \(\frac{1}{c}\) et on frappe une impasse. \[\frac{1}{c}x^2 + \frac{b}{c}x +1 = 0\]La ruse suivante nous permet d’arriver à nos fins : avant de diviser par \(c\), un changement de variable s’impose. Si \(c>0\), on pose \[x = \sqrt{c}z\]sinon, on pose \[x = \sqrt{-c}\,z\]Si \(c>0\), on obtient \[\left(\sqrt{c}z\right)^2 + b\left(\sqrt{c}z\right) + c = 0\] \[cz^{2}+b\sqrt{c}z + c = 0\]Si maintenant on divise par \(c\), on obtient à la fois un terme constant de \(1\) et un coefficient du terme au carré de \(1\) aussi. \[z^2 + \frac{b\sqrt{c}}{c}z + 1 = 0\]Si on préfère, on peut réécrire le terme du milieu comme \[z^2 + \frac{b\sqrt{c} \cdot \sqrt{c}}{c\cdot \sqrt{c}}z + 1 = 0\] \[z^2 + \frac{b}{\sqrt{c}}z + 1 = 0\]Si \(c\) est négatif, on obtient plutôt \begin{align*}\left(\sqrt{-c}\,z\right)^2 + b\left(\sqrt{-c}\,z\right) + c &= 0 \\ \\ -cz^2 + b\sqrt{-c}\,z + c &= 0 \\ \\ z^{2}+ \frac{b\sqrt{-c}}{-c}z-1 &= 0 \\ \\ z^{2}+\frac{b}{\sqrt{-c}}z-1&=0\end{align*}Un deuxième changement de variable nous permettra de résoudre l’équation. En posant \[\frac{b}{\sqrt{c}} = -\frac{2}{\sin(\theta)}\]ou \[\frac{b}{\sqrt{-c}} = \frac{2}{\tan\left(\theta\right)}\]selon le signe de \(c\), il sera possible ensuite de trouver les valeurs de \(z\) avec \[z = \tan\!\left(\frac{1}{2}\theta\right)\]
Des exemples !
Lorsque \(c>0\)
Lorsque \(c>0\), on sait que les deux solutions à l’équation quadratique seront toutes les deux positives ou toutes les deux négatives. Et c’est \[\tan^{2}\!\left(\frac{1}{2}\theta\right)-\frac{2}{\sin(\theta)}\cdot \tan\!\left(\frac{1}{2}\theta\right)+1=0\]qu’on utilise.
Résolvons \[x^{2}-8x+15=0\]Notons que puisque \(c = 15>0\) et \(b = -18<0\), les deux solutions seront des nombres positifs. Puisque \(15>0\), on effectue d’abord le changement de variable \[x = \sqrt{15}z\]pour obtenir \begin{align*}\left(\sqrt{15}z\right)^{2}-8\left(\sqrt{15}z\right) + 15 &= 0 \\ \\ 15z^{2}-8\sqrt{15}z + 15 &=0\end{align*}On divise chaque côté par \(15\) \[z^{2}-\frac{8\sqrt{15}}{15}z + 1 =0\] \[z^{2}-\frac{8}{\sqrt{15}}z + 1=0\]On pose ensuite \[-\frac{8}{\sqrt{15}}=-\frac{2}{\sin(\theta)}\]On résout \begin{align*}-\frac{8}{\sqrt{15}}&=-\frac{2}{\sin(\theta)} \\ \\ \frac{4}{\sqrt{15}}&=\frac{1}{\sin(\theta)} \\ \\ \sin(\theta)&=\frac{\sqrt{15}}{4}\end{align*}J’obtiens \begin{align*}\theta &= \arcsin\!\left(\frac{\sqrt{15}}{4}\right) \\ \\ &\approx 1,\!318116\end{align*}Je peux trouver l’autre angle avec \begin{align*}\theta &= \pi-\arcsin\!\left(\frac{\sqrt{15}}{4}\right) \\ \\ &\approx \pi-1,\!318116 \\ \\ &\approx 1,\!823477\end{align*}Puisque \[z = \tan\!\left(\frac{1}{2}\theta\right)\]Je trouve \begin{align*}z&\approx \tan\!\left(\frac{1}{2}\cdot 1,\!318116\right) \\ \\ &\approx \tan\left(0,\!659058\right) \\ \\ &\approx 0,\!774597\end{align*}dans le premier cas et \begin{align*}z&\approx \tan\!\left(\frac{1}{2}\cdot 1,\!823477\right) \\ \\ &\approx \tan\left(0,\!911738\right) \\ \\ &\approx 1,\!290994\end{align*}dans le deuxième. Un dernier changement de variable est nécessaire. Puisque \[x = \sqrt{15}z\]on trouve \begin{align*}x &\approx \sqrt{15}\cdot 0,\!774597 \\ \\ &\approx 3\end{align*}pour la première solution et \begin{align*}x &\approx \sqrt{15}\cdot 1,\!290994 \\ \\ &\approx 5\end{align*}On peut s’assurer, après substitutions, que les deux solutions à l’équation initiale sont bel et bien \(x=3\) et \(x=5\).
Si on résout plutôt \[x^2 + 14x + 45 = 0\]en observant que \(b = 14 >0\) et \(c = 45>0\), ici on sait que les deux solutions seront négatives. En effectuant les substitutions d’usage, on obtient d’abord \[z^2 + \frac{14}{\sqrt{45}}z + 1 = 0\]ce qui nous mène à \begin{align*}\theta &= \arcsin\!\left(-\frac{\sqrt{45}}{7}\right) \\ \\ &\approx -1,\!281044\end{align*}et \begin{align*}\theta &=\pi-\arcsin\!\left(-\frac{\sqrt{45}}{7}\right) \\ \\ &\approx 4,\!422637\end{align*}On obtient \[z \approx 0,\!745356\]ou \[z \approx -1,\!341641\]et \begin{align*}x &\approx \sqrt{45} \cdot -0,\!745356 \\ \\ &\approx -5\end{align*}et \begin{align*}x &\approx \sqrt{45}\cdot -1,\!341641 \\ \\ &\approx -9\end{align*}ce qui s’avère, après vérifications, être effectivement les solutions à l’équation.
Lorsque \(c<0\)
On peut aussi s’intéresser au cas où \(c<0\). Le lecteur aguerri peut se demander comment on fera pour trouver deux angles qui ont la même tangente. En fait, puisque la période de \(\tan\left(\theta\right)\) est \(\pi\) et celle de \(\tan\!\left(\frac{1}{2}\theta\right)\) est \(2\pi\), il suffira d’additionner ou de soustraire \(\pi\) à l’angle donné par l’arctangente.
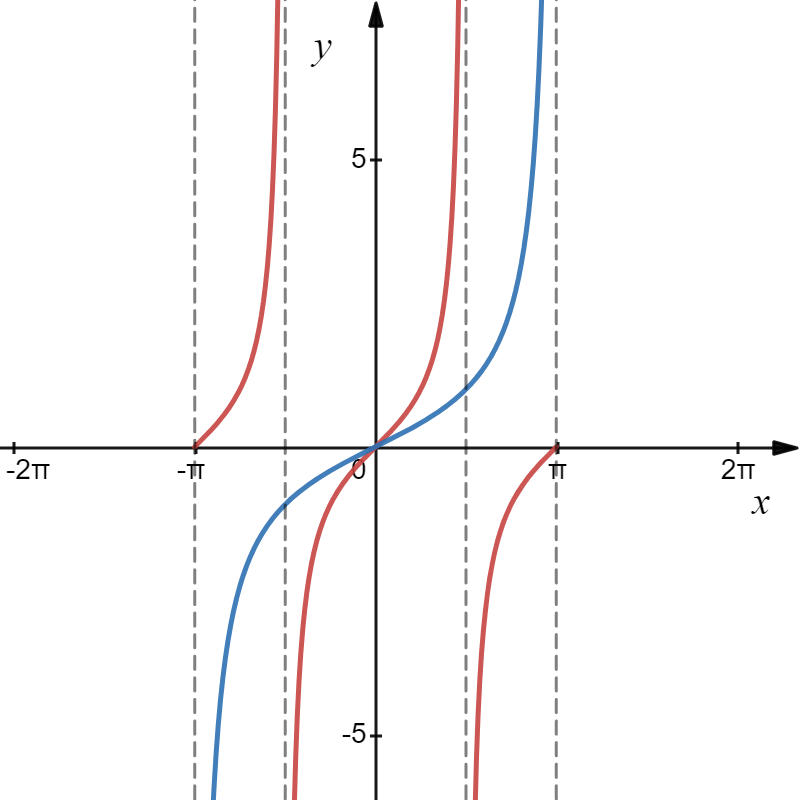
\(\textcolor{Red}{\tan\left(\theta\right)}\) en rouge et \(\textcolor{Blue}{\tan\!\left(\frac{1}{2}\theta\right)}\) en bleu
Résolvons \[x^{2}+x-6=0\]Notons que puisque \(c=-6>0\), les deux solutions seront de signes contraires. Puisque \(-6<0\), on effectue d’abord le changement de variable \[x = \sqrt{-(-6)}z = \sqrt{6}z\]pour obtenir \begin{align*}\left(\sqrt{6}z\right)^{2}+\left(\sqrt{6}z\right) -6 &= 0 \\ \\ 6z^{2}+\sqrt{6}z-6&=0\end{align*}On divise chaque côté par \(6\) \[z^{2}+\frac{\sqrt{6}}{6}z-1 =0\] \[z^{2}+\frac{1}{\sqrt{6}}z-1=0\]On pose ensuite \[\frac{1}{\sqrt{6}}=\frac{2}{\tan(\theta)}\]On résout \begin{align*}\frac{1}{\sqrt{6}}&=\frac{2}{\tan(\theta)} \\ \\ \tan(\theta)&=2\sqrt{6}\end{align*}J’obtiens \begin{align*}\theta &= \arctan\left(2\sqrt{6}\right) \\ \\ &\approx 1,\!369438\end{align*}Je peux trouver l’autre angle avec \begin{align*}\theta &= \arctan\!\left(2\sqrt{6}\right)-\pi \\ \\ &\approx 1,\!369438-\pi \\ \\ &\approx -1,\!772154\end{align*}Puisque \[z = \tan\!\left(\frac{1}{2}\theta\right)\]Je trouve \begin{align*}z&\approx \tan\!\left(\frac{1}{2}\cdot 1,\!369438\right) \\ \\ &\approx \tan\left(0,\!684719\right) \\ \\ &\approx 0,\!816497\end{align*}dans le premier cas et \begin{align*}z&\approx \tan\!\left(\frac{1}{2}\cdot (-1,\!772154)\right) \\ \\ &\approx \tan\left(-0,\!886077\right) \\ \\ &\approx -1,\!224745\end{align*}dans le deuxième. Un dernier changement de variable est nécessaire. Puisque \[x = \sqrt{6}z\]on trouve \begin{align*}x &\approx \sqrt{6}\cdot 0,\!816497 \\ \\ &\approx 2\end{align*}pour la première solution et \begin{align*}x &\approx \sqrt{6}\cdot (-1,\!224745) \\ \\ &\approx -3\end{align*}On peut s’assurer, après substitutions, que les deux solutions à l’équation initiale sont bel et bien \(x=2\) et \(x=-3\).
De l’utile au futile

Quel intérêt me direz-vous ? D’abord parce que ce n’est pas tous les jours qu’on a le plaisir de pouvoir écrire quelque chose comme \[x = \sqrt{c}\tan\!\left(\frac{1}{2}\arcsin\!\left(-\frac{2\sqrt{c}}{b}\right)\right)\] au lieu de \[x = \frac{-b+\sqrt{b^{2}-4c}}{2}\]Pour ma part, je trouve l’exercice fort captivant. Ensuite, de manière plus pragmatique, il semble que ces méthodes étaient plus en vogue lorsqu’il fallait chercher les valeurs des fonctions trigonométriques (ainsi que celles des logarithmes et des racines) dans les livres de tables et qu’il fallait effectuer les opérations à la règle à calcul. Bien que cela peut sembler complètement farfelu aujourd’hui, en théorie, dans certains cas, la méthode trigonométrique nécessite moins d’opérations et de recherches dans les tables que la méthode traditionnelle (jusqu’à 1/3 de recherches en moins), par exemple lorsque les coefficients sont des nombres décimaux du genre \[x^{2}-0,\!9751+ 0,\!2352=0\]et on dit qu’elle lui était parfois préférée pour cette raison.
Références : https://en.wikipedia.org/wiki/Quadratic_equation