The Dude – Page 42 – The Dude Minds…

La chaîne de Steiner et Géogébra4

Posted on 27/11/201122/09/2025 by The Dude

Géogébra4 nous permet désormais d’exporter des fichiers .GIF animés (génial !)

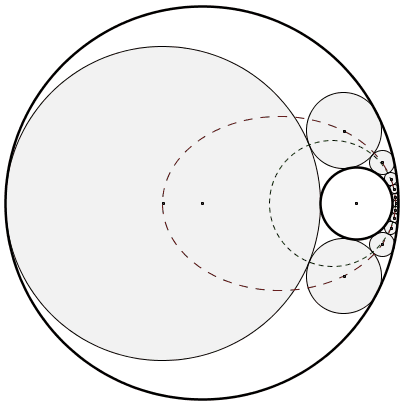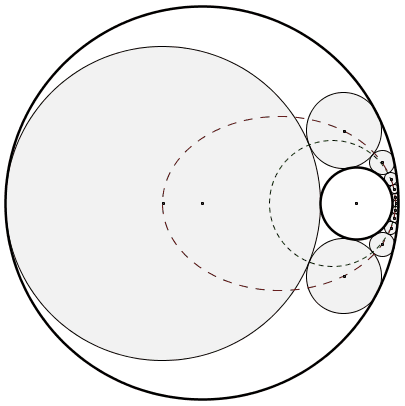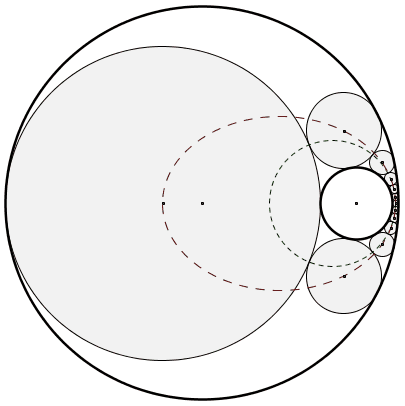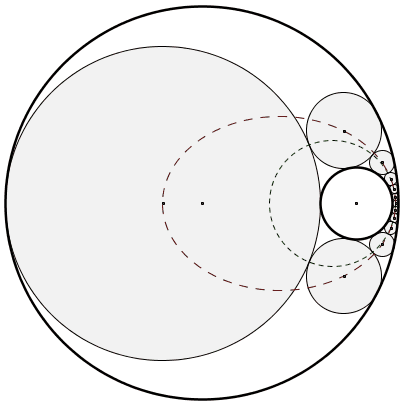
Voici une chaîne de 12 cercles de Steiner obtenue par inversion d’une figure régulière. La figure régulière (deux cercles concentriques et une chaîne de cercles isométriques tangents) et le cercle d’inversion ne sont pas affichés. Soyez patients, la figure est plutôt lourde, mais lorsqu’elle est chargée, le résultat est satisfaisant.

Le choix du premier des douze cercles de la chaîne est indifférent lorsque la chaîne se referme comme c’est le cas ici (porisme de Steiner). Sont aussi affichés sur la figure le cercle des points de tangence entre les cercles de la chaîne (en pointillés verts) et l’ellipse des centres des cercles de la chaîne (en pointillés rouges). Notez que les foyers de l’ellipse correspondent aux centres des grand et petit cercles initiaux.

La méthode somme-produit

Posted on 08/11/201122/09/2025 by The Dude

Problème : il faut factoriser \[6x^{2}-13x-5\]

Avec de petits nombres entiers, une des premières méthodes que l’on montre aux élèves est la méthode somme-produit. On cherche deux nombres dont la somme est \(-13\) et le produit est \(6 \times(-5)=-30\). Comme le produit est négatif, je cherche deux nombres de signes contraires. Après avoir cherché du côté des facteurs de \(30\), je trouve \(-15\) et \(2\). En effet, \[-15+2=-13\]et \[-15 \times 2=-30\]Je peux donc « désimplifier » le terme en \(x\) et écrire \[6x^{2}+2x-15x-5\]afin d’effectuer une mise en évidence double. C’est-à-dire \[2x(3x+1)-5(3x+1)\]puis \[(3x+1)(2x-5)\]Or, comme le mentionne avec pertinence James Tanton, si on demande à des enseignants du secondaire

pourquoi ça marche ?

on obtient généralement une réponse qui ressemble à ceci : on commence avec \[(ax+b)(cx+d)\]où \(a\), \(b\), \(c\), et \(d\) sont des entiers. On effectue le produit \[ax^{2}+(ad+bc)x + bd\]Le coefficient du terme du premier degré est composé de la somme de deux nombres, à savoir \(ad\) et \(bc\). On voit aussi que le produit du coefficient du terme du deuxième degré et du terme constant est égal au produit de ces deux nombres \[ad \cdot bc = ac \cdot bd\]la multiplication étant commutative et associative.

Et voilà pourquoi ça marche !

Or cela ne répond pas effectivement à la question. On montre en réalité la réciproque de l’énoncé initial. Comme le souligne Tanton, il serait important (au moins pour l’enseignant, pas pour l’élève) de montrer l’implication directe. C’est-à-dire que si l’on a \[ax^{2}+bx+c\]et que \[b = p+q\]et \[ac = pq\]et où \(a\), \(b\), \(c\), \(p\) et \(q\) sont des entiers, alors le trinôme se décompose en deux facteurs à coefficients entiers.

On a donc \[ax^{2}+(p+q)x+c\] \[ax^{2}+px+qx+c\]On pose \(j\) comme le plus grand commun diviseur de \(a\) de \(p\). On a donc \[a = jk\]pour un certain entier \(k\). Comme \(ac = pq\), on a \[jkc = pq\]Évidemment, \(j\) divise \(p\), donc \(\frac{p}{j}\) est un entier. Or, comme \(k\) ne divise pas \(\frac{p}{j}\) , mais que \[kc = \frac{p}{j}q\]alors on a que \(k\) divise \(q\). C’est-à-dire que \(\frac{q}{k}\) est aussi un entier et que \[c = \frac{p}{j} \cdot \frac{q}{k}\]On a donc \[jkx^{2}+px + qx + \frac{p}{j}\cdot \frac{q}{k}\]et en effectuant une mise en évidence double \[jx\left(kx + \frac{p}{j}\right) + \frac{q}{k}\left(kx + \frac{p}{j}\right)\]on obtient \[\left(kx + \frac{p}{j}\right)\left(jx+\frac{q}{k}\right)\]c’est-à-dire deux facteurs à coefficients entiers.