Il est assez facile de montrer que si l’on a une fonction quadratique et qu’en observant sa table de valeurs, il y a des bonds constants du côté de la variable indépendante, alors on observera des bonds entre les bonds constants du côté de la variable dépendante. Et si les bonds constants de la variable indépendante sont de \(1\), et que la règle de la fonction quadratique est \[f(x) = ax^{2}+bx + c\]alors les bonds entre les bonds du côté de la variable dépendante auront une valeur de \(2a\). Un de mes collègues avait une question fort pertinente, c’est-à-dire celle-ci :
Réciproquement, si l’on a une fonction dans laquelle, pour des bonds constants de \(1\) du côté de la variable indépendante, on a des bonds entre les bonds constants d’une valeur de \(2a\) du côté de la variable dépendante, alors montrez qu’il s’agit d’une fonction quadratique.
On a
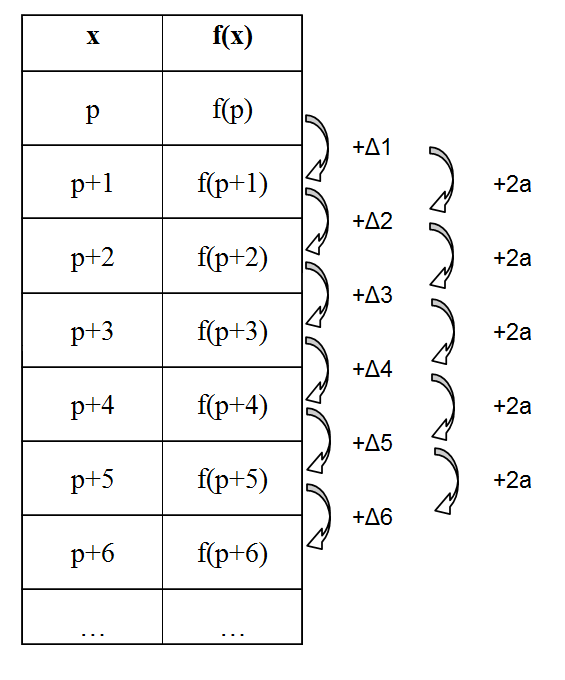On tire donc \begin{align*}f(p)&=f(p) \\ \\ f(p+1) &= f(p) + \Delta_{1} \\ \\ f(p+2) &= f(p) + \Delta_{1}+\Delta_{2} \\ \\ f(p+3) &= f(p) + \Delta_{1} + \Delta_{2} + \Delta_{3} \\ \\ f(p+4)&=f(p)+\Delta_{1}+\Delta_{2}+\Delta_{3}+\Delta_{4} \\ \\ &\dots\end{align*}
ce qui est équivalent à \begin{align*}f(p)&=f(p) \\ \\ f(p+1) &= f(p) + \Delta_{1} \\ \\ f(p+2) &= f(p) + \Delta_{1}+(\Delta_{1}+2a) \\ \\ f(p+3) &= f(p) + \Delta_{1} + (\Delta_{1}+2a) + (\Delta_{1}+4a) \\ \\ f(p+4)&=f(p)+\Delta_{1}+(\Delta_{1}+2a)+(\Delta_{1}+4a)+(\Delta_{1}+6a) \\ \\ &\dots\end{align*}Le terme général sera donc \[f(x) = f(p) + \Delta_{1}+(\Delta_{1}+2a) + (\Delta_{1}+4a) + \ \dots \ + (\Delta_{1}+(x-p-1)(2a))\]En regroupant les \(\Delta_{1}\) (il y en aura \(x-p\)) \[f(x) = f(p) + (x-p)\Delta_{1}+2a+4a+\ \dots \ + (x-p-1)(2a)\]puis en effectuant la mise en évidence de \(2a\), on obtient \[f(x) = f(p) + (x-p)\Delta_{1}+(2a)(1 + 2 + 3 + \ \dots \ + (x-p-1))\]La somme entre parenthèses est celle des \(x-p-1\) premiers entiers \[f(x) = f(p) + (x-p)\Delta_{1}+(2a)\left(\frac{(x-p-1)(x-p)}{2}\right)\]En développant le produit au numérateur \[f(x) = f(p) + (x-p)\Delta_{1}+ (2a)\left(\frac{p+p^{2}-x-2px+x^{2}}{2}\right)\]et en distribuant le facteur \(2a\) dans la parenthèse, et en effectuant les produits restants, on obtient \[f(x) = f(p) + \Delta_{1}x-\Delta_{1}p + ap + ap^{2}-ax-2apx+ax^{2}\]En réarrangeant les termes, on constate qu’il s’agit bien d’une fonction quadratique \[f(x) = ax^{2}+(\Delta_{1}-a-2ap)x + (f(p) + ap^{2}+ap -\Delta_{1}p)\]dont le coefficient du terme au carré est bien \(a\) !
Par exemple, si l’on a
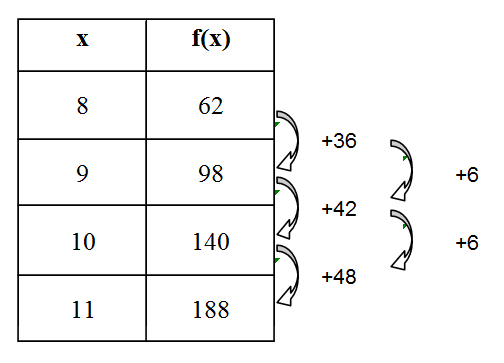On aura, en prenant \(a=3\), \(p=8\), \(f(p) = 62\) et \(\Delta_{1}=36\), \[f(x) = 3x^{2}+(36-3-2\cdot3\cdot 8)x + (62 + 3\cdot 8^{2}+3\cdot 8-36 \cdot 8)\]ce qui correspond à \[f(x) = 3x^{2}-15x-10\]la règle de la fonction quadratique.
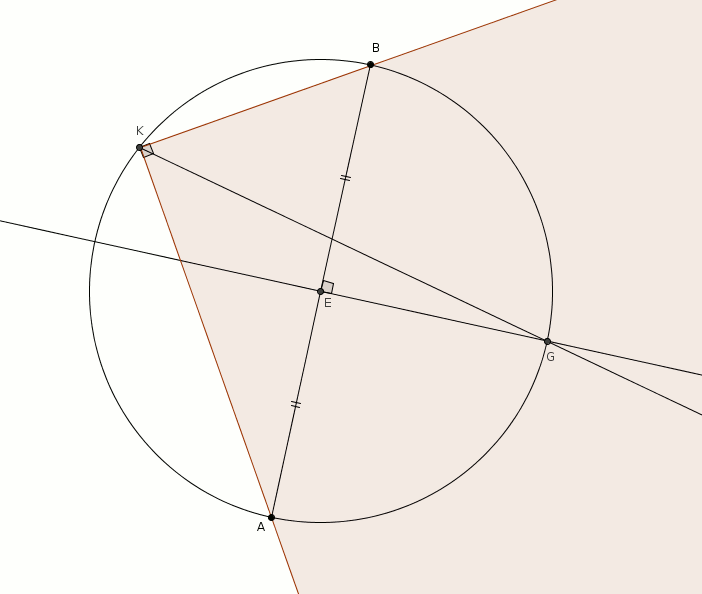
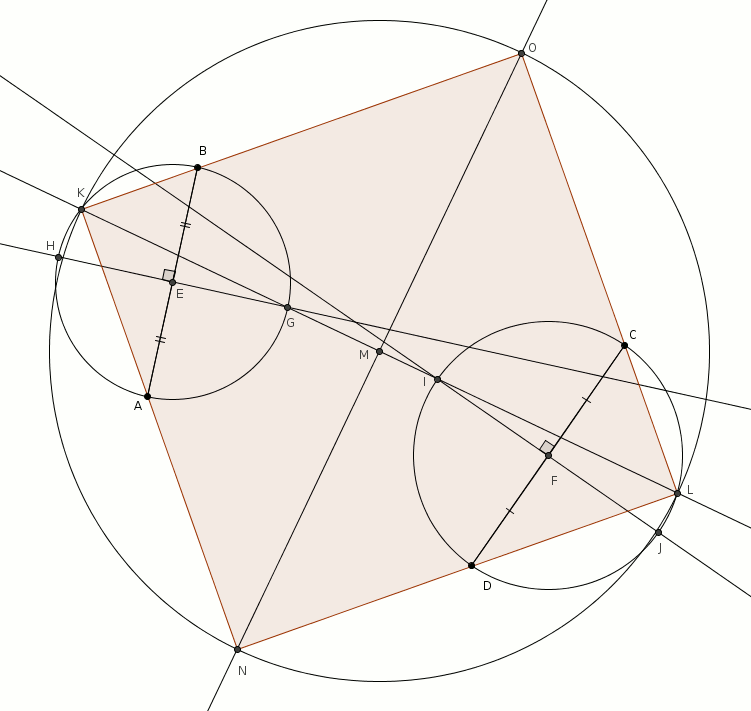
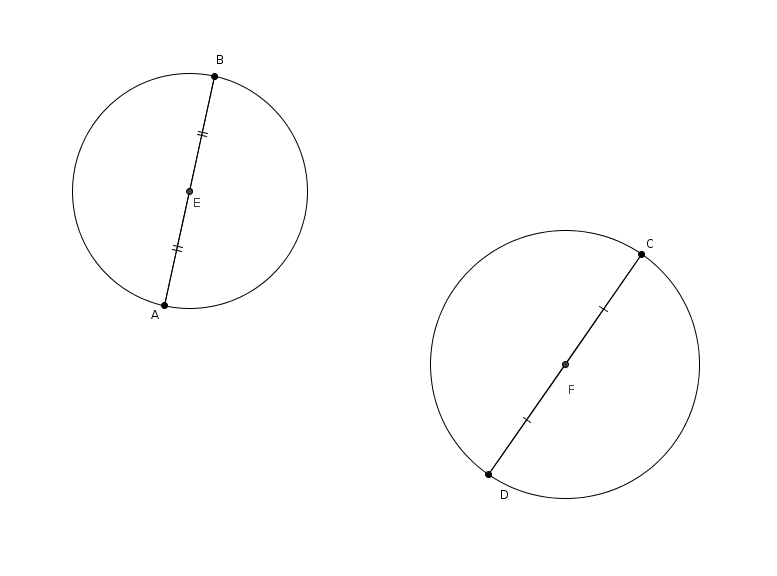On trace ensuite les perpendiculaires à \(\overline{AB}\) par \(E\) et à \(\overline{CD}\) par \(F\). Ces perpendiculaires coupent les cercles respectivement en \(H\) et \(G\) et en \(I\) et \(J\) (tel qu’illustré ci-dessous).
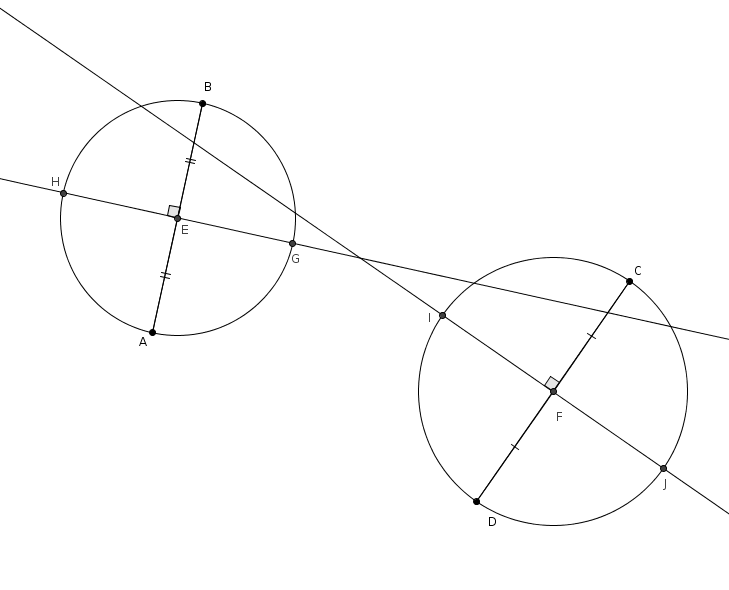On choisit ensuite deux de ces points de telle sorte que la droite qui passe par ces points coupe les cercles à deux autres endroits. Dans notre exemple, on choisit les points \(G\) et \(I\) puisque la droite \(GI\) coupe les deux cercles à deux autres endroits, respectivement en \(K\) et \(L\). Nous avons vu que la droite \(GK\) supportait une diagonale du carré et, dans l’autre cercle, la droite \(IL\) supportait aussi une diagonale du carré. L’astuce est ici de faire coïncider ces deux diagonales qui ne sont en effet qu’une seule : la droite \(KL\) supporte une des deux diagonales du carré… et \(K\) et \(L\) sont deux sommets opposés du carré.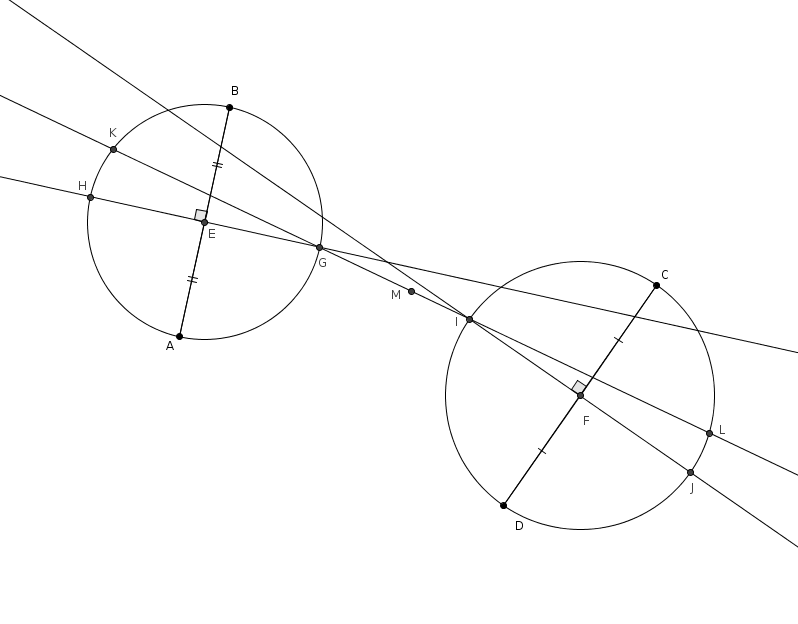
puis une autre avec les mêmes points
ou encore avec quatre points colinéaires !