Les bonds entre les bonds…

Il est assez facile de montrer que si l’on a une fonction quadratique et qu’en observant sa table de valeurs, il y a des bonds constants du côté de la variable indépendante, alors on observera des bonds entre les bonds constants du côté de la variable dépendante.  Et si les bonds constants de la variable indépendante sont de $1$, et que la règle de la fonction quadratique est $$f(x)=a{x}^2+bx+c$$alors les bonds entre les bonds du côté de la variable dépendante auront une valeur de $2a$.  Un de mes collègues avait une question fort pertinente, c’est-à-dire celle-ci :

Réciproquement, si l’on a une fonction dans laquelle, pour des bonds constants de 1 du côté de la variable indépendante, on a des bonds entre les bonds constants d’une valeur de 2a du côté de la variable dépendante, alors montrez qu’il s’agit d’une fonction quadratique.

On a

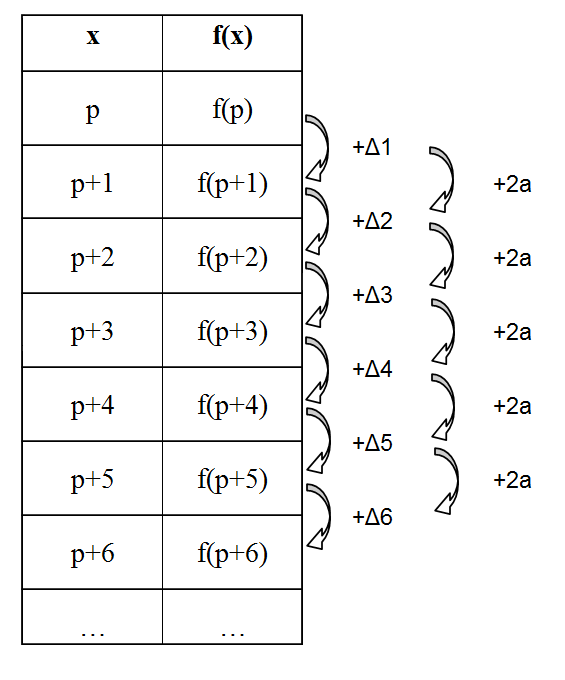On tire donc $$\begin{array}{rl}f(p)& =f(p)\\ \\ f(p+1)& =f(p)+{\mathrm{\Delta }}_1\\ \\ f(p+2)& =f(p)+{\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2\\ \\ f(p+3)& =f(p)+{\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2+{\mathrm{\Delta }}_3\\ \\ f(p+4)& =f(p)+{\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2+{\mathrm{\Delta }}_3+{\mathrm{\Delta }}_4\\ \\ & \dots \end{array}$$
ce qui est équivalent à $$\begin{array}{rl}f(p)& =f(p)\\ \\ f(p+1)& =f(p)+{\mathrm{\Delta }}_1\\ \\ f(p+2)& =f(p)+{\mathrm{\Delta }}_1+({\mathrm{\Delta }}_1+2a)\\ \\ f(p+3)& =f(p)+{\mathrm{\Delta }}_1+({\mathrm{\Delta }}_1+2a)+({\mathrm{\Delta }}_1+4a)\\ \\ f(p+4)& =f(p)+{\mathrm{\Delta }}_1+({\mathrm{\Delta }}_1+2a)+({\mathrm{\Delta }}_1+4a)+({\mathrm{\Delta }}_1+6a)\\ \\ & \dots \end{array}$$Le terme général sera donc $$f(x)=f(p)+{\mathrm{\Delta }}_1+({\mathrm{\Delta }}_1+2a)+({\mathrm{\Delta }}_1+4a)+\dots +({\mathrm{\Delta }}_1+(x-p-1)(2a))$$En regroupant les ${\mathrm{\Delta }}_1$ (il y en aura $x-p$) $$f(x)=f(p)+(x-p){\mathrm{\Delta }}_1+2a+4a+\dots +(x-p-1)(2a)$$puis en effectuant la mise en évidence de $2a$, on obtient $$f(x)=f(p)+(x-p){\mathrm{\Delta }}_1+(2a)(1+2+3+\dots +(x-p-1))$$La somme entre parenthèses est celle des $x-p-1$ premiers entiers $$f(x)=f(p)+(x-p){\mathrm{\Delta }}_1+(2a)\left(\frac{(x-p-1)(x-p)}{2}\right)$$En développant le produit au numérateur $$f(x)=f(p)+(x-p){\mathrm{\Delta }}_1+(2a)\left(\frac{p+p^2-x-2px+x^2}{2}\right)$$et en distribuant le facteur 2a dans la parenthèse, et en effectuant les produits restants, on obtient $$f(x)=f(p)+{\mathrm{\Delta }}_{1}x-{\mathrm{\Delta }}_{1}p+ap+a{p}^2-ax-2apx+a{x}^2$$En réarrangeant les termes, on constate qu’il s’agit bien d’une fonction quadratique $$f(x)=a{x}^2+({\mathrm{\Delta }}_1-a-2ap)x+(f(p)+a{p}^2+ap-{\mathrm{\Delta }}_{1}p)$$dont le coefficient du terme au carré est bien $a$ !

Par exemple, si l’on a

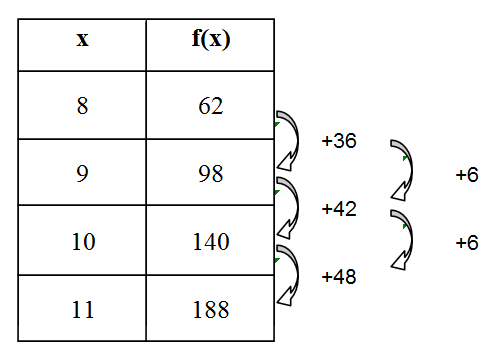On aura, en prenant $a=3$, $p=8$, $f(p)=62$ et ${\mathrm{\Delta }}_1=36$, $$f(x)=3x^2+(36-3-2\cdot 3\cdot 8)x+(62+3\cdot 8^2+3\cdot 8-36\cdot 8)$$ce qui correspond à $$f(x)=3x^2-15x-10$$la règle de la fonction quadratique.