Le crible d’Érathostène est un procédé qui permet de trouver tous les nombres premiers inférieurs à un certain entier naturel \(N\). C’est un algorithme simple et efficace. Voici ce que le génie d’Euler fait d’un algorithme simple et efficace.
Considérez la fonction \(\zeta\) ci-dessus \[\zeta(s) = \sum_{n=1}^{\infty}\frac{1}{n^{s}}\]ou \[\zeta(s) = 1 + \frac{1}{2^{s}} + \frac{1}{3^{s}} + \frac{1}{4^{s}} + \frac{1}{5^{s}} + \frac{1}{6^{s}} + \frac{1}{7^{s}} + \frac{1}{8^{s}} + \frac{1}{9^{s}} + \frac{1}{10^{s}} + \frac{1}{11^{s}} + \frac{1}{12^{s}} + \, \dots\]On définit cette fonction pour tout \(s>1\). En effet pour \(s=1\), on retrouve la série harmonique, divergente. Pour des valeurs de \(s\) comprises strictement entre \(0\) et \(1\), en comparant la série précédente terme à terme avec la série harmonique, on obtient des dénominateurs systématiquement plus petits, c’est-à-dire des fractions systématiquement plus grandes. Il n’y a donc aucun doute que la série diverge lorsque s prend des valeurs strictement comprises entre \(0\) et \(1\). Enfin, pour \(s=0\), on obtient \[\zeta(0) = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + \, \dots\]qui diverge aussi.
Pour des valeurs de \(s\) plus grandes que \(1\), la série converge. Euler a trouvé plusieurs valeurs exactes lorsque \(s\) est pair, notamment lorsque \(s=2\) (le problème de Bâle), et pour les \(s\) impairs il y a encore beaucoup de questions qui résistent à l’assaut des mathématiciens. Or donc, en reprenant \[\zeta(s) = 1 + \frac{1}{2^{s}} + \frac{1}{3^{s}} + \frac{1}{4^{s}} + \frac{1}{5^{s}} + \frac{1}{6^{s}} + \frac{1}{7^{s}} + \frac{1}{8^{s}} + \frac{1}{9^{s}} + \frac{1}{10^{s}} + \frac{1}{11^{s}} + \frac{1}{12^{s}} + \, \dots \]on commence par multiplier chaque côté par \(\dfrac{1}{2^{s}}\) \[\left(\frac{1}{2^{s}}\right) \zeta(s) = \left(\frac{1}{2^{s}}\right)\left(1 + \frac{1}{2^{s}} + \frac{1}{3^{s}} + \frac{1}{4^{s}} + \frac{1}{5^{s}} + \frac{1}{6^{s}} + \frac{1}{7^{s}} + \frac{1}{8^{s}} + \frac{1}{9^{s}} + \frac{1}{10^{s}}+ \, \dots \right)\]ce qui fait en distribuant \[\left(\frac{1}{2^{s}}\right) \zeta(s) = \frac{1}{2^{s}} + \frac{1}{4^{s}} + \frac{1}{6^{s}} + \frac{1}{8^{s}} + \frac{1}{10^{s}} + \frac{1}{12^{s}} + \frac{1}{14^{s}} + \frac{1}{16^{s}} + \frac{1}{18^{s}} + \, \dots \]On soustrait le résultat précédent à \(\zeta(s)\) \[\zeta(s)-\left(\frac{1}{2^{s}}\right)\zeta(s) = 1 + \frac{1}{3^{s}} + \frac{1}{5^{s}} + \frac{1}{7^{s}} + \frac{1}{9^{s}} +\frac{1}{11^{s}} + \frac{1}{13^{s}} + \frac{1}{15^{s}} + \frac{1}{17^{s}} + \frac{1}{19^{s}} + \, \dots \]ce qui fait après une mise en évidence simple à gauche\[\left(1-\frac{1}{2^{s}}\right)\zeta(s) = 1 + \frac{1}{3^{s}} + \frac{1}{5^{s}} + \frac{1}{7^{s}} + \frac{1}{9^{s}} +\frac{1}{11^{s}} + \frac{1}{13^{s}} + \frac{1}{15^{s}} + \frac{1}{17^{s}} + \frac{1}{19^{s}} + \, \dots\]Remarquez les dénominateurs à droite : tous les multiples de \(2\) disparaissent. On multiplie le résultat obtenu par \(\dfrac{1}{3^{s}}\) \[\left(\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s) = \left(\frac{1}{3^{s}}\right)\left(1 + \frac{1}{3^{s}} + \frac{1}{5^{s}} + \frac{1}{7^{s}} + \frac{1}{9^{s}} + \frac{1}{11^{s}} + \frac{1}{13^{s}} + \frac{1}{15^{s}} + \frac{1}{17^{s}} +\, \dots \right)\]ce qui fait en distribuant\[\left(\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s) = \frac{1}{3^{s}} + \frac{1}{9^{s}} + \frac{1}{15^{s}} + \frac{1}{21^{s}} + \frac{1}{27^{s}} +\frac{1}{33^{s}} + \frac{1}{39^{s}} + \frac{1}{45^{s}} +\, \dots \]On soustrait ce nouveau résultat à\[\left(1-\frac{1}{2^{s}}\right)\zeta(s) = 1 + \frac{1}{3^{s}} + \frac{1}{5^{s}} + \frac{1}{7^{s}} + \frac{1}{9^{s}} +\frac{1}{11^{s}} + \frac{1}{13^{s}} + \frac{1}{15^{s}} + \frac{1}{17^{s}} + \frac{1}{19^{s}} + \, \dots\]afin d’obtenir\[\left(1-\frac{1}{2^{s}}\right)\zeta(s)-\left(\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s)=1 + \frac{1}{5^{s}} + \frac{1}{7^{s}} + \frac{1}{11^{s}} + \frac{1}{13^{s}} + \frac{1}{17^{s}} + \, \dots \]Après mise en évidence simple, on a \[\left(1-\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s) = 1+\frac{1}{5^{s}} + \frac{1}{7^{s}} + \frac{1}{11^{s}} + \frac{1}{13^{s}} + \frac{1}{17^{s}} + \frac{1}{19^{s}}+\frac{1}{23^{s}}+\, \dots\]On avait déjà éliminé tous les multiples de \(3\) qui sont aussi des multiples de \(2\) à la première étape. Mais il restait les multiples de \(3\) non multiples de \(2\). Là on vient d’éliminer tous ces multiples. Il ne reste aucun multiple de \(3\) aux dénominateurs, à droite. Une régularité commence à apparaître : c’est le crible, version améliorée (puisqu’on élimine les nombres à éliminer qu’une seule fois). On multiplie le résultat précédent par \(\dfrac{1}{5^{s}}\) \[\left(\frac{1}{5^{s}}\right)\left(1-\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s) = \left(\frac{1}{5^{s}}\right) \left(1+\frac{1}{5^{s}} + \frac{1}{7^{s}} + \frac{1}{11^{s}} + \frac{1}{13^{s}} + \frac{1}{17^{s}} + \frac{1}{19^{s}}+\, \dots\right)\]ce qui fait en distribuant \[\left(\frac{1}{5^{s}}\right)\left(1-\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s) = \frac{1}{5^{s}} + \frac{1}{25^{s}}+ \frac{1}{35^{s}} + \frac{1}{55^{s}} + \frac{1}{65^{s}} + \frac{1}{85^{s}} + \, \dots \]Encore une fois, on soustrait ce dernier résultat à \[\left(1-\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s) = 1+\frac{1}{5^{s}} + \frac{1}{7^{s}} + \frac{1}{11^{s}} + \frac{1}{13^{s}} + \frac{1}{17^{s}} + \frac{1}{19^{s}}+\frac{1}{23^{s}}+\, \dots\]ce qui donne \begin{align*}\left(1-\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s)-\left(\frac{1}{5^{s}}\right)\left(1-\frac{1}{3^{s}}\right)\left(1- \frac{1}{2^{s}}\right)\zeta(s) &=\left(1-\frac{1}{5^{s}}\right)\left(1-\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s) \\ \\ &= 1 + \frac{1}{7^{s}} + \frac{1}{11^{s}} + \frac{1}{13^{s}} + \frac{1}{17^{s}} + \frac{1}{19^{s}} + \, \dots \end{align*}
Ainsi dans\[\left(1-\frac{1}{5^{s}}\right)\left(1-\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s) = 1+\frac{1}{7^{s}}+\frac{1}{11^{s}} + \frac{1}{13^{s}} + \frac{1}{17^{s}}+\frac{1}{19^{s}}+ \, \dots \]ous les multiples de \(5\) qui restaient aux dénominateurs, à droite, disparaissent. À ce moment, dans une étape typiquement eulérienne, Euler explique : en continuant de la sorte aussi longtemps qu’il le faut, en passant tour à tour les nombres premiers, on arrive à \[\dots \, \left(1-\frac{1}{13^{s}}\right)\left(1-\frac{1}{11^{s}}\right)\left(1-\frac{1}{7^{s}}\right)\left(1-\frac{1}{5^{s}}\right)\left(1-\frac{1}{3^{s}}\right)\left(1-\frac{1}{2^{s}}\right)\zeta(s) = 1\]En isolant \(\zeta(s)\), il obtient \[\zeta(s) = \frac{1}{\left(1-\frac{1}{2^{n}}\right)\left(1-\frac{1}{3^{n}}\right)\left(1-\frac{1}{5^{n}}\right)\left(1-\frac{1}{7^{n}}\right)\left(1-\frac{1}{11^{n}}\right)\left(1-\frac{1}{13^{n}}\right) \, \dots}\]ou plus élégamment \[\zeta(s) = \frac{1}{1-\cfrac{1}{2^{s}}} \times \frac{1}{1-\cfrac{1}{3^{s}}} \times \frac{1}{1-\cfrac{1}{5^{s}}}\times \frac{1}{1-\cfrac{1}{7^{s}}} \times \frac{1}{1-\cfrac{1}{11^{s}}} \times \frac{1}{1-\cfrac{1}{13^{s}}} \times \, \dots \]Avec une notation plus concise, on peut même réécrire le résultat précédent comme ceci \[\zeta(s) = \left(1-2^{-s}\right)^{-1}\left(1-3^{-s}\right)^{-1}\left(1-5^{-s}\right)^{-1}\left(1-7^{-s}\right)^{-1}\left(1-11^{-s}\right)^{-1}\left(1-13^{-s}\right)^{-1} \, \dots \]ce qui donne \[\zeta(s) = \prod_{p}\left(1-p^{-s}\right)^{-1}\]un produit infini étendu à tous les nombres premiers \(p\).
En se rappelant aussi que \[\zeta(s) = \sum_{n=1}^{\infty}\frac{1}{n^{s}}\]on obtient cette jolie égalité\[\sum_{n=1}^{\infty}n^{-s} = \prod_{p}\left(1-p^{-s}\right)^{-1}\]une somme infinie à gauche et un produit infini à droite.
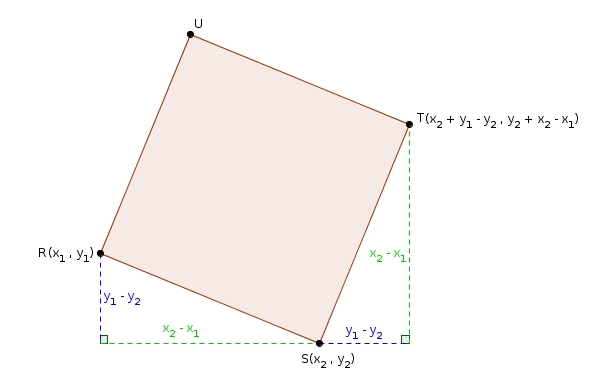
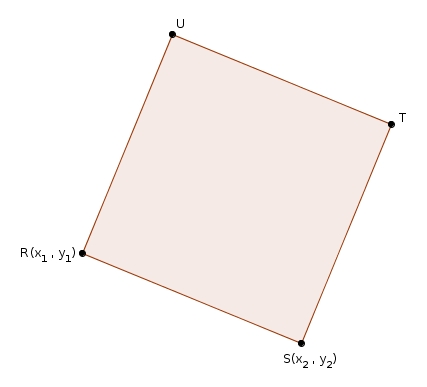 dans lequel les coordonnées de \(R\) et \(S\) sont respectivement \((x_{1},\, y_{1})\) et \((x_{2},\, y_{2})\).
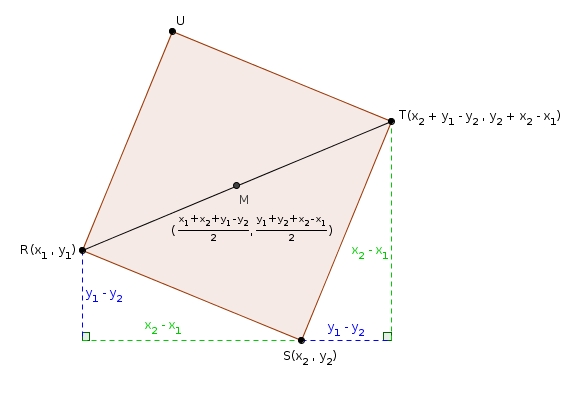
dans lequel les coordonnées de \(R\) et \(S\) sont respectivement \((x_{1},\, y_{1})\) et \((x_{2},\, y_{2})\).