Voici une preuve assez simple de l’irrationalité du nombre \(e\) (considérant une connaissance préalable des factorielles et des séries géométriques). À l’instar de certaines démonstrations parfois faites avec les élèves montrant que \(\sqrt{2}\) et \(\log_{10}(2)\) sont des nombres irrationnels, il s’agit d’une preuve par l’absurde.
En se rappelant que le nombre \(e\) est égal à la série infinie suivante \[e = \frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!} + \frac{1}{3!} + \ \dots \ + \frac{1}{n!} + \ \dots\]avec \(0! = 1\), on appelle \(S_{n}\) la somme partielle des termes de cette série. C’est-à-dire la somme des \(n\) premiers termes de cette série telle que \[S_{n} = \frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+ \ \dots \ +\frac{1}{(n-1)!}+\frac{1}{n!}\]Remarquons que pour tout \(n = 1, \ 2, \ 3, \ 4, \ \dots \ \) on a \[S_{n}<e\]Cela implique aussi que \[0< e-S_{n}\]Que reste-t-il lorsqu’on soustrait \(S_{n}\) à \(e\) ? Il reste \[0<e-S_{n}=\frac{1}{(n+1)!}+\frac{1}{(n+2)!}+\frac{1}{(n+3)!}+\ \dots\]ce qui est égal à \[0<e-S_{n}=\frac{1}{(n+1)!}+\frac{1}{(n+1)!(n+2)} + \frac{1}{(n+1)!(n+2)(n+3)}+ \ \dots\]En effectuant une mise en évidence simple, on obtient \[0<e-S_{n}=\frac{1}{(n+1)!}\left(1+\frac{1}{n+2}+\frac{1}{(n+2)(n+3)}+ \ \dots \right)\]Nous posons alors l’inéquation suivante, étape clé de la démarche,\begin{align*}0<e-S_{n}&=\frac{1}{(n+1)!}\left(1+\frac{1}{n+2}+\frac{1}{(n+2)(n+3)}+ \ \dots\right) \\ \\ &<\frac{1}{(n+1)!}\left(1+\frac{1}{n+1} + \frac{1}{(n+1)(n+1)} + \ \dots\right)\end{align*}puisque, toujours avec \(n = 1,\ 2, \ 3, \ 4, \ \dots \ \) les dénominateurs de chaque terme étant respectivement strictement plus petits, les fractions sont respectivement strictement plus grandes \begin{align*}\frac{1}{n+1}&>\frac{1}{n+2} \\ \\ \frac{1}{(n+1)(n+1)}&>\frac{1}{(n+2)(n+3)} \\ \\ \frac{1}{(n+1)(n+1)(n+1)} &> \frac{1}{(n+2)(n+3)(n+4)}\\ \\ &\dots \end{align*}Or, cette nouvelle expression est constituée d’une série géométrique infinie (dans la parenthèse). Le premier terme \(a\) de cette série géométrique est \(1\) et la raison \(r\) de cette série géométrique est \[r=\frac{1}{n+1}\]Or, comme \(n = 1,\ 2, \ 3, \ 4, \ \dots \ \) il se trouve très certainement que \[r<1\]et on peut donc exprimer la somme de cette série géométrique infinie de façon succincte, c’est \[\frac{a}{1-r}\]On trouve \begin{align*}0<e-S_{n}&=\frac{1}{(n+1)!}\left(1+\frac{1}{n+2}+\frac{1}{(n+2)(n+3)}+\ \dots\right)\\ \\ &<\frac{1}{(n+1)!}\left(1+\frac{1}{n+1}+\frac{1}{(n+1)(n+1)}+\ \dots \ \right) = \frac{1}{(n+1)!}\left(\frac{1}{1-\frac{1}{n+1}}\right)\end{align*}En reprenant seulement ce qui nous intéresse \[0<e-S_{n}<\frac{1}{(n+1)!}\left(\frac{1}{1-\frac{1}{n+1}}\right)\]et en mettant sur dénominateur commun \[0<e-S_{n}<\frac{1}{(n+1)!}\left(\frac{1}{\frac{n+1}{n+1}-\frac{1}{n+1}}\right)\]et en effectuant la soustraction, on obtient \[0<e-S_{n}<\frac{1}{(n+1)!}\left(\frac{1}{\frac{n}{n+1}}\right)\]et enfin en simplifiant \[0<e-S_{n}<\frac{1}{(n+1)!}\left(\frac{n+1}{n}\right)\]Comme \[(n+1)! = n!\,(n+1)\]le numérateur \(n+1\) s’annule avec le même facteur du dénominateur. Il reste \[0<e-S_{n}<\frac{1}{n!\cdot n}\]En multipliant par \(n!\) de chaque côté (\(n!\) étant strictement positif, on ne change pas les signes \(<\) de côté) on obtient \[0<n!\,(e-S_{n})<\frac{1}{n}\]Notons à ce moment que cette inégalité tient pour tout \(n = 1, \ 2, \ 3, \ 4, \ \dots \ \)
Supposons que \(e\) soit un nombre rationnel. Il pourrait alors s’écrire comme une fraction d’entiers. Sachant que la valeur de \(e\) est entre \(2\) et \(3\), supposons que la fraction réduite représentant le nombre \(e\) soit \[e = \frac{p}{q}\]avec \[p, \, q \in \mathbb{N}\]et \[\text{pgcd}(p,\, q) =1 \]Cette supposition nous mènera à une contradiction.
Puisque l’inégalité ci-haut tient pour tout \(n = 1, \ 2, \ 3, \ 4, \ \dots \ \) choisissons \(n\) tel que \[n>q\]Certainement,\[q>1\]sans quoi \(e\) serait un entier (ce qui n’est clairement pas le cas). On en déduit donc que \[n>1\]et que \[\frac{1}{n}<1\]c’est-à-dire une fraction strictement plus petite que \(1\). Dans l’inégalité suivante \[0<n!\,(e-S_{n})<\frac{1}{n}<1\]l’expression du milieu \[n!\,(e-S_{n})\]est comprise en \(0\) et \(1\) (exclusivement) et ne peut donc pas être un nombre entier. En remplaçant \(e\) par la fraction réduite qui lui est égale, obtient \[n!\,(e-S_{n}) = n!\left(\frac{p}{q}-S_{n}\right)\]puis en développant \(S_{n}\) \begin{align*}n!\,(e-S_{n})&= n!\left(\frac{p}{q}-S_{n}\right) \\ \\ &=n!\left(\frac{p}{q}-\left(\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+ \ \dots \ +\frac{1}{n!}\right)\right) \\ \\ &=n!\left(\frac{p}{q}\right)-n!\left(1+1+\frac{1}{2!}+\ \dots \ + \frac{1}{n!}\right)\end{align*}Enfin réexprimant le premier terme et en distribuant \(n!\) dans la deuxième parenthèse on obtient \[n!\, (e-S_{n}) = \left(\frac{n!}{q}\right)p-\left(n! + n! + \frac{n!}{2!}+\ \dots \ + \frac{n!}{n!}\right)\]Or, on a choisit \[n>q\]Cela implique que \(q\) divise \(n!\) puisque \[n! = 1 \cdot 2 \cdot 3 \cdot \ \dots \ \cdot q \cdot \ \dots \ \cdot n\]Le premier terme \[\left(\frac{n!}{q}\right)p\]est donc un nombre entier. Par ailleurs, le même argument s’applique à chaque terme à l’intérieur de la parenthèse : \(n!\) est certainement un entier, \(2!\) divise \(n!\), c’est donc aussi un entier, \(3!\) divise \(n!\), encore là un entier… Et ce jusqu’au dernier terme, \(n!\) divisant certainement \(n!\), il s’agit encore d’un entier. L’expression entre parenthèse \[\left(n! + n! + \frac{n!}{2!} + \ \dots \ + \frac{n!}{n!}\right)\]est donc aussi un nombre entier. Aussi surprenant que cela puisse paraître, l’expression \[\left(\frac{n!}{q}\right)p-\left(n!+n!+\frac{n!}{2!}+ \ \dots \ + \frac{n!}{n!}\right)\]est un entier. Or comme \[n!\, (e-S_{n})\]n’est pas un entier, et que nous avions plus haut \[n! \, (e-S_{n}) = \left(\frac{n!}{q}\right)p-\left(n!+n!+\frac{n!}{2!}+ \ \dots \ + \frac{n!}{n!}\right)\]nous obtenons la contradiction recherchée ! Le nombre \(e\) est irrationnel et ne peut s’exprimer comme un quotient d’entiers.
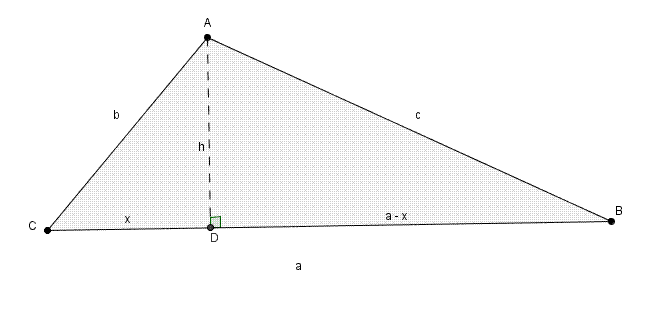On peut d’abord trouver l’aire \(K\) du triangle \[K = \frac{ah}{2}\]