Author: The Dude

En quatrième secondaire on travaille avec les élèves les conditions minimales de similitude des triangles. Une attention particulière est portée aux relations métriques dans les triangles rectangles dans lesquels on a tracé la hauteur issue de l’angle droit (ou la hauteur relative à l’hypoténuse). Voici un petit résultat qui fait changement des exercices du manuel. Les élèves apprécient.

Considérez le triangle rectangle \(ABC\) ci-dessous (rectangle en \(C\))

On trace la hauteur issue de l’angle droit. Elle coupe \(\overline{AB}\) de façon perpendiculaire en \(D\). Le “petit” triangle \(ACD\) et le “grand” triangle \(ABC\) sont tous les deux rectangles et partagent tous les deux l’angle \(A\). Il sont donc semblables par le cas de similitude AA. \[\triangle ABC \sim \triangle ACD\]Les côtés homologues des triangles semblables sont dans le même rapport. Considérons les “petites” cathètes et les hypoténuses des deux triangles. On obtient la proportion suivante\[\frac{m\overline{AC}}{m\overline{AD}} = \frac{m\overline{AB}}{m\overline{AC}}\]de laquelle on tire \[\left(m\overline{AC}\right)^{2} = m\overline{AB}\cdot m\overline{AD}\]Le “moyen” triangle \(CBD\) et le “grand” triangle \(ABC\) sont tous les deux rectangles et partagent tous les deux l’angle \(B\). Il sont donc semblables par le cas de similitude AA.\[\triangle ABC \sim \triangle CBD\]En considérant les “grandes” cathètes et les hypoténuses des deux triangles, on obtient la proportion suivante\[\frac{m\overline{BC}}{m\overline{BD}} = \frac{m\overline{AB}}{m\overline{BC}}\]de laquelle on tire \[\left(m\overline{BC}\right)^{2}=m\overline{AB}\cdot m\overline{BD}\]En additionnant les deux résultats précédents on obtient \[\left(m\overline{AC}\right)^2 + \left(m\overline{BC}\right)^2 = m\overline{AB}\cdot m\overline{AD} + m\overline{AB}\cdot m\overline{BD}\]et en effectuant la mise en évidence simple à droite\[\left(m\overline{AC}\right)^2 + \left(m\overline{BC}\right)^2 = m\overline{AB}\cdot \left(m\overline{AD} + m\overline{BD}\right)\]Les segments \(AD\) et \(BD\) forment justement le segment \(AB\), l’hypoténuse du grand triangle rectangle. On a donc en substituant \[\left(m\overline{AC}\right)^2 + \left(m\overline{BC}\right)^2 = m\overline{AB}\cdot m\overline{AB}\]ou tout simplement \[\left(m\overline{AC}\right)^2 + \left(m\overline{BC}\right)^2 = \left(m\overline{AB}\right)^2 \]… la relation de Pythagore ! \[a^2 + b^2 = c^2\]

La forme canonique de la fonction exponentielle est \[g(x) = a\cdot c^{b(x-h)}+k\]où \(c\) est la base de la fonction de la fonction exponentielle (strictement positive et différente de \(1\)). On utilise les lettres usuelles \(a\), \(b\), \(h\), \(k\) pour désigner les paramètres multiplicatifs et additifs des variables dépendantes et indépendantes. Comme avec bien d’autres fonctions, il s’avère que certains paramètres sont superflus. En transformant le produit à l’exposant en exponentiation, on obtient \[g(x) = a\cdot \left(c^{b}\right)^{(x-h)}+k\]Il nous est donc possible de choisir une nouvelle base, \(c_{1}\), telle que \[c_{1} = c^{b}\]Notre fonction initiale devient alors \[g(x) = a\cdot \left(c_{1}\right)^{(x-h)}+k\]En transformant la somme à l’exposant en produit de deux puissances de même base on obtient \[g(x) = a\cdot \left(c_{1}\right)^{x}\cdot \left(c_{1}\right)^{-h}+k\]que je réécris comme \[g(x) = a\cdot \left(c_{1}\right)^{-h}\cdot \left(c_{1}\right)^{x}+k\]Il nous est maintenant possible de choisir un nouveau paramètre \(a\), appelons-le \(a_{1}\), tel que \[a_{1}=a\cdot\left(c_{1}\right)^{-h}\]Notre fonction devient alors \[g(x)=a_{1}\cdot\left(c_{1}\right)^{x}+k\]que j’appellerai la forme canonique réduite de la fonction exponentielle. Il est donc toujours possible de poser \(b=1\) et \(h=0\) dans le cas d’une fonction exponentielle en jouant avec le paramètre \(a\) et la base \(c\).

Qu’en est-il de la fonction logarithmique, la réciproque de la fonction exponentielle ? La forme canonique de la fonction logarithmique est \[f(x) = a\log_{c}\left(b(x-h)\right)+k\]où, encore une fois, \(c\) est la base de la fonction logarithmique (strictement positive et différente de \(1\)).

Cette fonction possèdent-elles des paramètres superflus ? Avec l’exponentielle, nous avions d’abord effectué un changement de base. Est-il possible d’emprunter une démarche semblable ? On change la base de la fonction logarithmique pour la nouvelle base \(c_{1}\). La loi du changement de base avec les logarithmes nous donne \[f(x) = a\left(\frac{\log_{c_{1}}\left(b(x-h)\right)}{\log_{c_{1}}(c)}\right) + k\]que je réécris comme \[f(x) = \frac{a}{\log_{c_{1}}(c)} \cdot \log_{c_{1}}\left(b(x-h)\right) + k\]En posant le coefficient égal à \(1\), \[\frac{a}{\log_{c_{1}}(c)}=1\]et en isolant le logarithme, on obtient \[a = \log_{c_{1}}(c)\]En transformant sous la forme exponentielle on obtient \[\left(c_{1}\right)^{a} =c\]Et en isolant \(c_{1}\) on obtient \[c_{1} = c^{\frac{1}{a}}\]c’est-à-dire \[c_{1} = \sqrt[a]{c}\]si \(a\) est positif et \[c_{1} = \sqrt[-a]{\frac{1}{c}}\]si \(a\) est négatif.

En choisissant la bonne base, il est donc toujours possible de rendre le paramètre \(a=1\). En effet, en choisissant \(c_{1}\) de telle manière, notre fonction initiale devient \[f(x) = \log_{c_{1}}\left(b(x-h)\right)+k\]Notons ensuite que par définition de logarithme, on a \[k = \log_{c_{1}}\left(\left(c_{1}\right)^{k}\right)\](et, au passage, pas de problème si \(k\) est négatif).

En remplaçant dans \[f(x) = \log_{c_{1}}\left(b(x-h)\right)+k\]on obtient \[f(x) = \log_{c_{1}}\left(b(x-h)\right) + \log_{c_{1}}\left(\left(c_{1}\right)^{k}\right)\]En exprimant la somme des deux logarithmes avec le logarithme du produit on obtient \[f(x) = \log_{c_{1}}\left(b\cdot \left(c_{1}\right)^{k}\cdot (x-h)\right)\]En choisissant un nouveau paramètre \(b\), appelons-le \(b_{1}\), tel que \[b_{1}= b\cdot \left(c_{1}\right)^{k}\]notre fonction initiale devient \[f(x) = \log_{c_{1}}\left(b_{1}(x-h)\right)\]que j’appelle la forme canonique réduite de la fonction logarithmique.

Si on place un capital initial \(C_{0}\) à un taux d’intérêt annuel \(i\) composé \(n\) fois par année, alors après avoir composé \(t\) fois l’intérêt, on aura accumulé un (fameux) montant \(C(t)\) de \[C(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}\]C’est la formule bien connue de l’intérêt composé. Par exemple, si on place \(5\, 000\) dollars pendant \(10\) ans à un taux d’intérêt annuel de \(2\%\) (donc \(i = 0,\!02\)) composé chaque mois (donc \(n=12\)), on obtient au bout des \(10\) ans (c’est-à-dire après avoir composé les intérêts \(12 \times 10 = 120\) fois) \[C(120) =5000 \left(1+\frac{0,\!02}{12}\right)^{12\cdot 10} \approx 6\,106,\!00\]C’est environ \(1\,106\) dollars de plus, une augmentation de près de \(22\%\) par rapport au capital initialement investi ! Pas mal ! C’est aussi \(106\) dollars de plus que si on avait placé cet argent à intérêt simple. Vous me direz : « Placer 5000$ en 2010 pendant 10 ans à ton âge, c’est de la science-fiction ! »

En effet, la (ma ?) tendance actuelle est plutôt à l’emprunt de capital ! Et lorsqu’on emprunte, on doit éventuellement rembourser. Supposons que l’on rembourse, à chaque fois que l’on compose les intérêts (chaque trimestre ? mois ? semaine ?), un certain montant \(P\). Et considérons une fonction \(f\) qui exprime notre capital dû.

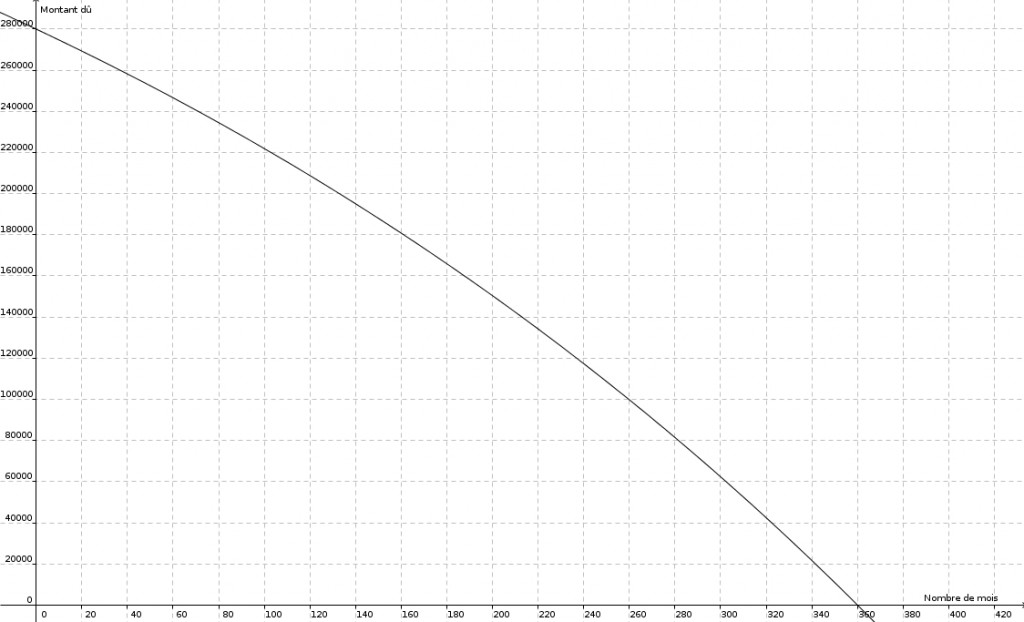
Au départ on a tout simplement \[f(0) = C_{0}\]Après un premier calcul des intérêts, \(\left(1 +\frac{i}{n}\right)\), on rembourse un montant \(P\). \[f(1) = C_{0}\left(1 + \frac{i}{n}\right)-P\]Au deuxième versement, c’est \[f(2) = \left(C_{0}\left(1 + \frac{i}{n}\right)-P\right)\left(1 + \frac{i}{n}\right)-P\]En distribuant le facteur \(\left(1+\frac{i}{n}\right)\) on obtient \[f(2) = C_{0}\left(1+\frac{i}{n}\right)^{2}-P\left(1 + \frac{i}{n}\right)-P\]Au troisième,\[f(3) = \left(C_{0}\left(1 + \frac{i}{n}\right)^{2}-P\left(1+\frac{i}{n}\right)-P\right)\left(1 + \frac{i}{n}\right)-P\]et encore une fois en distribuant, \[f(3) = C_{0}\left(1+\frac{i}{n}\right)^{3}-P\left(1+\frac{i}{n}\right)^{2}-P\left(1+\frac{i}{n}\right)-P\]Au quatrième calcul des intérêts, \[f(4)=\left(C_{0}\left(1+\frac{i}{n}\right)^{3}-P\left(1+\frac{i}{n}\right)^{2}-P\left(1+\frac{i}{n}\right)-P\right)\left(1+\frac{i}{n}\right)-P\]et en distribuant, \[f(4) = C_{0}\left(1+\frac{i}{n}\right)^{4}-P\left(1+\frac{i}{n}\right)^{3}-P\left(1+\frac{i}{n}\right)^{2}-P\left(1+\frac{i}{n}\right)-P\]Une tendance se dégage. Il apparait de plus en plus clair qu’au \(t\)^e calcul des intérêts, on aura \[f(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}-P\left(1+\frac{i}{n}\right)^{t-1}\ – \ \dots \ – \ P\left(1+\frac{i}{n}\right)^{2}-P\left(1+\frac{i}{n}\right)-P\]Une mise en évidence simple de \(-P\) nous donne \[f(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}-P\left(\left(1+\frac{i}{n}\right)^{t-1} \ + \ \dots \ + \ \left(1 + \frac{i}{n}\right)^{2}+\left(1+\frac{i}{n}\right) + 1\right)\]L’expression dans la grande parenthèse est une série géométrique finie de premier terme 1 et de raison (1 + i/n). Nous pouvons exprimer sa somme de façon plus concise. On obtient \[f(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}-P\left(\frac{1-\left(1+\frac{i}{n}\right)^{t}}{1-\left(1+\frac{i}{n}\right)}\right)\]Enfin, une petite simplification nous donne \[f(t)=C_{0}\left(1+\frac{i}{n}\right)^{t}-P\left(\frac{1-\left(1+\frac{i}{n}\right)^{t}}{1-1-\frac{i}{n}}\right)\]puis \[f(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}+P\left(\frac{n}{i}\right)\left(1-\left(1+\frac{i}{n}\right)^{t}\right)\]Voilà donc l’expression recherchée. Maintenant, comment calculer la valeur de \(P\) afin qu’à terme, on ait remboursé la totalité de notre emprunt ? Posons \[f(t) = 0\]On a alors \[C_{0}\left(1+\frac{1}{n}\right)^{t}+P\left(\frac{n}{i}\right)\left(1-\left(1+\frac{i}{n}\right)^{t}\right) = 0\]On soustrait \(C_{0}\left(1+\frac{i}{n}\right)^{t}\)de chaque côté de l’égalité \[P\left(\frac{n}{i}\right)\left(1-\left(1+\frac{i}{n}\right)^{t}\right)=-C_{0}\left(1+\frac{i}{n}\right)^{t}\]puis on divise \[P=\frac{-C_{0}\left(\frac{i}{n}\right)\left(1+\frac{i}{n}\right)^{t}}{1-\left(1+\frac{i}{n}\right)^{t}}\]En multipliant par \(-1\) en haut et en bas, on obtient l’expression légèrement plus élégante suivante \[P= \frac{C_{0}\left(\frac{i}{n}\right)\left(1+\frac{i}{n}\right)^{t}}{\left(1+\frac{i}{n}\right)^{t}-1}\]Cette dernière formule nous donne la valeur de \(P\) en fonction de \(C_{0}\), \(i\), \(n\) et \(t\). Supposons que l’on emprunte \(280\, 000\) dollars sur une période de \(30\) ans à un taux annuel de \(2,\!5\%\), composé chaque mois, le remboursement mensuel s’élèvera à \[P = \frac{280\,000\left(\frac{0,025}{12}\right)\left(1+\frac{0,025}{12}\right)^{(12\cdot 30)}}{\left(1+\frac{0,025}{12}\right)^{(12\cdot 30)}-1} \approx 1\,106,\!34\]Et l’expression \[f(t) = C_{0}\left(1+\frac{i}{n}\right)^{t}+P\left(\frac{n}{i}\right)\left(1-\left(1+\frac{i}{n}\right)^{t}\right)\]ou, de manière équivalente, \[f(t) = \left(C_{0}-P\cdot \left(\frac{n}{i}\right)\right)\cdot\left(1+\frac{i}{n}\right)^{t}+P\cdot\left(\frac{n}{i}\right)\]nous permet alors de représenter graphiquement la situation (le montant dû en fonction du temps)

La formule de l’intérêt composé est aussi une occasion de découvrir une constante mathématique bien connue.

On décide de placer notre capital pour une durée de \(s\) année. Au bout de ces \(s\) années, avec des intérêts composés \(n\) fois par année, on aura effectué \(n\cdot s\) calculs d’intérêt (\(t = ns\)). Supposons que l’on place \(5\,000\)$ pendant \(10\) ans à un taux d’intérêt annuel de \(2\%\), composé une seule fois par année. Après \(10\) ans on obtient \[5\,000\left(1+\frac{0,\!02}{1}\right)^{1\cdot 10} \approx 6\,094,\!97\]Si les intérêts sont calculés chaque trimestre (\(n=4\)), on obtient \[5\,000\left(1+\frac{0,\!02}{4}\right)^{4\cdot 10} \approx 6\,103,\!97\]c’est-à-dire environ \(9\) dollars de plus (par rapport à \(n=1\)). En calculant les intérêts chaque mois, on obtient \[5\,000\left(1+\frac{0,\!02}{12}\right)^{12\cdot 10} \approx 6\,106,\!00\]résultat déjà calculé ci-haut. C’est un peu plus de \(2\) dollars de plus que pour des intérêts calculés chaque trimestre. On peut conjecturer que plus l’intérêt est calculé un grand nombre de fois par année, plus le montant accumulé sera grand sur cette période. Cependant, l’impact semble devenir de plus en plus minime. Si les intérêts sont calculés chaque jour, on obtient \[5\,000 \left(1+\frac{0,\!02}{365}\right)^{365\cdot 10} \approx 6\,106,\!98\]c’est-à-dire une augmentation de seulement \(98\) cents sur une période de \(10\) ans (par rapport à des intérêts composés chaque mois). Des intérêts composés chaque seconde ? Pourquoi pas !\[5\,000 \left(1+ \frac{0,\!02}{31\,536\,000}\right)^{31\,536\,000 \cdot 10} \approx 6\,107,\!02\]Avec les montants en jeu, on gagne… \(4\) cents ! Sur \(10\) ans ! Dix ans pendant lesquels chaque année on calcule les intérêts plus de \(31\) millions de fois. Le phénomène semble se rapprocher d’une limite. Qu’arrive-t-il alors à cette expression \[f(s) = C_{0}\left(1+\frac{i}{n}\right)^{ns}\]lorsqu’on fait tendre \(n\) à l’infini ? En faisant tendre \(n\) à l’infini, on considère des intérêts composés de façon continue. Afin de rendre les choses claires et élégantes, on introduit une nouvelle variable \(u\) telle que \[u =\frac{n}{i}\]Si \[n\to \infty\]alors il est clair que \[u \to \infty\]lui aussi. Cela implique également que \[n = ui\]et \[\frac{i}{n} = \frac{1}{u}\]On peut donc réécrire \[f(s) = C_{0}\left(1 + \frac{i}{n}\right)^{ns}\]lorsque \[n\to \infty\]comme \[f(s) = C_{0}\left(1+\frac{1}{u}\right)^{uis}\]lorsque \[n\to \infty\]En transformant le produit à l’exposant en exponentiation on obtient \[f(s) = C_{0}\left(\left(1+\frac{1}{u}\right)^{u}\right)^{is}\]Et comme \[u\to \infty\]on a \[\left(1+\frac{1}{u}\right)^{u} \to e\]La base naturelle \(e\) fait son apparition ! On obtient donc plus simplement \[f(s) = C_{0}\, e^{is}\]pour calculer les intérêts composés de façon continue.