Author: The Dude

La preuve de la formule quadratique n’est jamais facile à faire ni à comprendre pour les élèves de quatrième secondaire. Elle tombe d’ailleurs généralement assez rapidement dans l’oubli (la preuve, pas la formule). J’ai donné plus tôt ces deux démonstrations. Dans la première, classique, on met \(a\) en évidence et on complète le carré. Dans la deuxième, on utilise un changement de variable pour faire disparaître le terme du premier degré. En voici une troisième particulièrement élégante. On complète ici aussi le carré.

On a \[ax^2 + bx + c = 0\]Afin d’obtenir un carré parfait, on voudrait que le premier terme soit un carré. \(x\) est déjà au carré alors on multipliera chaque terme par \(a\) afin d’obtenir \[a^{2}x^{2}+abx + ac = 0\]On voudrait ensuite que le coefficient du deuxième terme soit pair pour ne pas s’empêtrer inutilement de fractions. On pourrait donc multiplier chaque terme par \(2\). Sauf qu’en multipliant par \(2\), le premier terme ne serait plus un carré. On décide donc de multiplier chaque terme par le plus petit carré pair, c’est-à-dire par \(4\). On obtient \[4a^{2}x^{2}+4abx + 4ac = 0\]Si l’expression de gauche est un carré, alors le premier terme est un carré de côté \(2ax\) tel que représenté dans l’illustration suivante

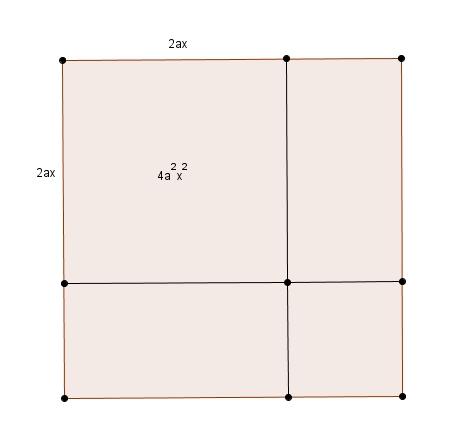Les deux rectangles isométriques forment le deuxième terme. Ces rectangles ont donc une aire de \(2abx\). Or, comme ils ont déjà une longueur de \(2ab\), leur largeur sera de \(b\).

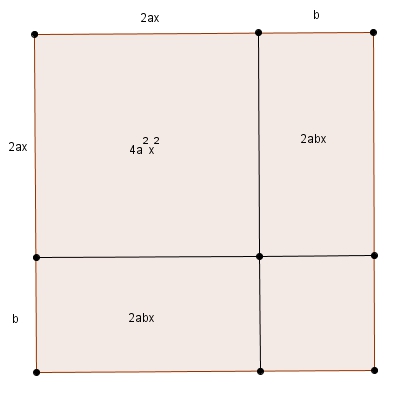ce qui nous laisse avec un dernier carré d’aire \(b^{2}\).

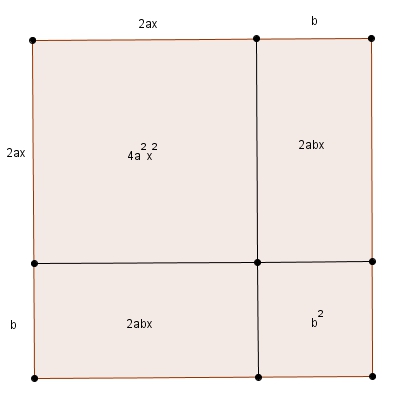Or, dans\[4a^{2}x^{2}+4abx+4ac=0\] le dernier terme n’est pas \(b^2\). Le dernier terme est plutôt \(4ac\). Nous retrancherons donc \(4ac\) de chaque côté et nous ajouterons \(b^{2}\) de chaque côté (afin d’avoir un trinôme carré parfait à gauche). On obtient \[4a^{2}x^{2}+4abx=-4ac\]puis\[4a^{2}x^{2}+4abc+b^{2}=b^{2}-4ac\]Le membre de gauche se factorise (c’est le carré) \[\left(2ax+b\right)^{2}=b^{2}-4ac\]Et là on obtient, en extrayant la racine carrée de chaque côté (attention aux signes) \[2ax+b=\pm\sqrt{b^{2}-4ac}\]puis en soustrayant \(b\) de chaque côté \[2ax=-b\pm\sqrt{b^{2}-4ac}\]et puis en divisant par \(2a\) de chaque côté \[x = \frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\]La formule quadratique, pas de chichi.

La somme des inverses des entiers naturels non-nuls (la série harmonique) tend vers l’infini (voir ici pour la preuve de Nicole Oresme). On dit que la série est divergente. Ainsi, \[\lim_{n\to \infty}\sum_{i=1}^{n}\frac{1}{i}=\infty\]Le grand Euler a montré (une première fois à vingt-huit ans dans une preuve particulièrement eulérienne en 1735, puis à nouveau avec une preuve plus rigoureuse en 1741) que la somme des inverses des carrés des entiers naturels non-nuls converge vers une valeur, aussi surprenante soit-elle d’ailleurs, cette valeur. C’est le problème de Bâle. On écrit \[\lim_{n\to \infty}\sum_{i=1}^{n}\frac{1}{i^{2}}= \frac{\pi^{2}}{6}\]Deux séries intimement liées, l’une divergente, l’autre convergente. Avec cette malice toute mathématique, on décide d’accoler un carré de côté \(1\) et d’aire \(1\) à un carré de côté \(\frac{1}{2}\) et d’aire \(\frac{1}{4}\). On accole ensuite un carré de côté \(\frac{1}{3}\) et d’aire \(\frac{1}{9}\). Puis on accole un carré de côté \(\frac{1}{4}\) et d’aire \(\frac{1}{16}\). On continue le processus aussi longtemps qu’on le souhaite tel qu’illustré dans l’image ci-dessous …

Et il se trouve qu’en continuant le processus aussi longtemps que désiré, la mesure d’un côté de cette figure, le côté inférieur, tend vers l’infini (c’est la série harmonique) alors que son aire tend vers un nombre bien fini, bien tangible (c’est le problème de Bâle).

C’est aussi le problème un peu gênant du pauvre peintre qui a besoin d’une quantité finie de peinture pour peindre l’intérieur des carrés mais d’une quantité infinie de peinture pour seulement en tracer les contours.

Référence : A harmonic serie paradox via Let’s play math

Voici une petite construction facile et intéressante à réaliser. Sur une feuille de papier tracez un cercle et découpez-le.

Identifier trois points sur la circonférence du cercle. Faites en sorte que les points puissent former un triangle acutangle

de telle sorte que

Rabattez ensuite deux des côtés du triangle et notez le point d’intersection des arcs de cercles.

puis rabattez ensuite le troisième côté…

Dépliez. Le point d’intersection correspond à l’orthocentre, le point d’intersection des trois hauteurs.

Ah ! Et maintenant, pourquoi ça marche ? Cela ne m’apparaissait pas nécessairement évident de prime abord, mais il suffit de regarder les bons angles dans les bons triangles (comme d’habitude !) Considérons le triangle \(ABC\) dans le cercle suivant. J’ai tracé les hauteurs \(AH\) et \(BE\) qui se rencontrent en \(G\).

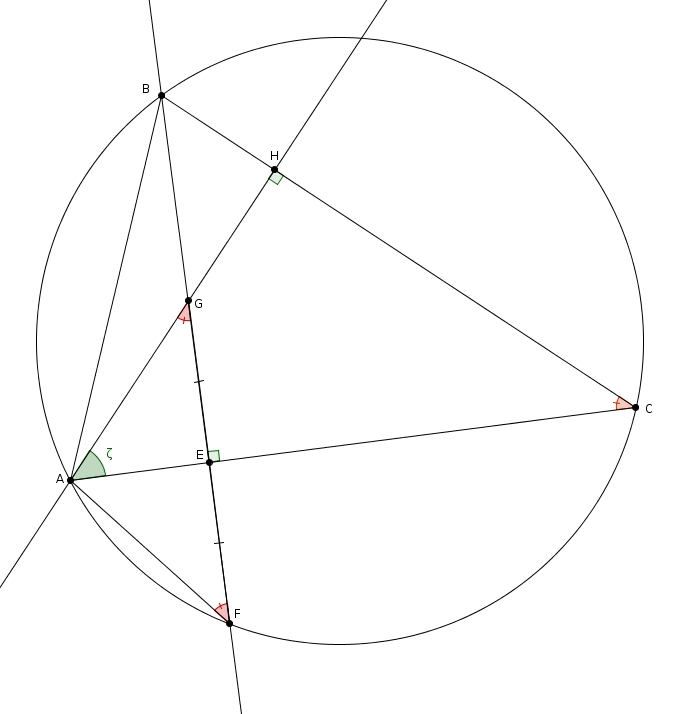Il faut montrer que \[m\overline{EG}=m\overline{EF}\]Les angles \(AFB\) et \(ACB\) sont isométriques puisque ce sont des angles inscrits qui interceptent le même arc. Moins évident est le fait que l’angle \(AGF\) est aussi isométrique à l’angle \(ACB\). Les triangles \(GAE\) et \(CAH\) sont tous deux rectangles (par définition de hauteur). Ces deux triangles partagent aussi l’angle \(GAE\) (noté \(\zeta\) sur le schéma). Ils sont donc semblables par le cas AA. Et comme dans les triangles semblables les angles homologues sont isométriques, cela implique que l’angle \(AGE\) est isométrique à l’angle \(ACH\).

Le triangle \(AGF\) est donc isocèle. \(AE\) est une hauteur du triangle isocèle. Or, dans un triangle isocèle, cette hauteur est aussi médiatrice. Et par définition de médiatrice, on obtient le résultat recherché.

Référence : Orthocenter Curiosities sur “I hope this old train breaks down…”