Author: The Dude

Examinons d’abord cette proposition : le lieu de points du centre \(C\) d’un cercle \(C_{2}\) (variable) tangent à un grand cercle \(C_{1}\) (fixe) et passant par un point \(A\), à l’intérieur de \(C_{1}\), est une ellipse. Soit \(O\) le centre de \(C_{1}\). On peut construire le cercle tangent \(C_{2}\) de cette façon :

1. tracer la droite \(OB\), avec \(B\) sur \(C_{1}\).
2. tracer le segment \(AB\).
3. tracer la médiatrice de \(\overline{AB}\), elle coupe \(OB\) en \(C\) : c’est le centre recherché.
4. tracer \(C_{2}\), de centre \(C\) et de rayon \(CA\).

On obtient

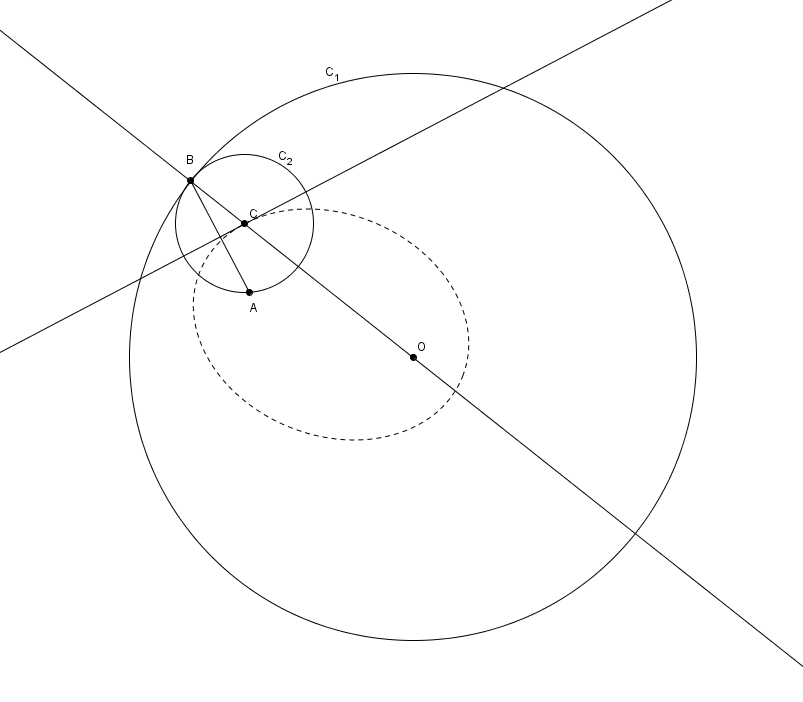
On trouve \[m\overline{CA} + m\overline{CO}=m\overline{BC}+m\overline{CO}=m\overline{BO}\]Or \(\overline{BO}\) est le rayon du grand cercle \(C_{1}\) (fixe). C’est donc une constante. Le point \(C\) est donc, par définition, sur une ellipse dont les foyers sont les points \(A\) et \(O\).\[m\overline{CA}+m\overline{CO} = \text{ Constante}\]

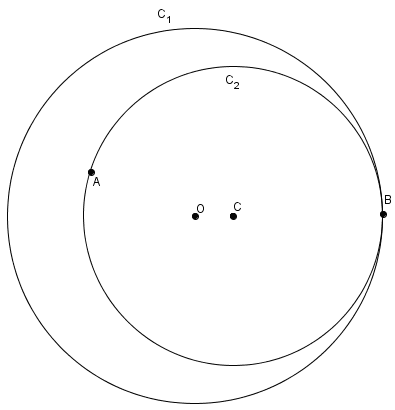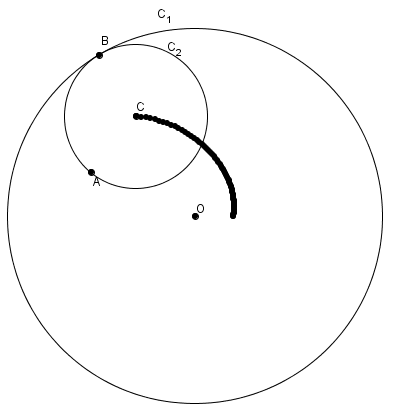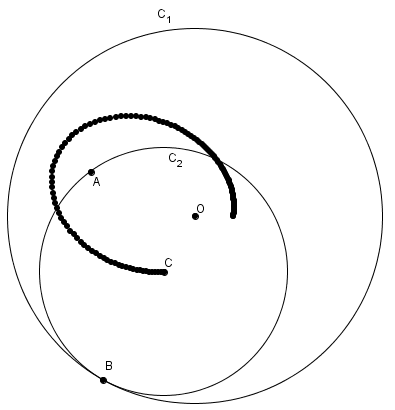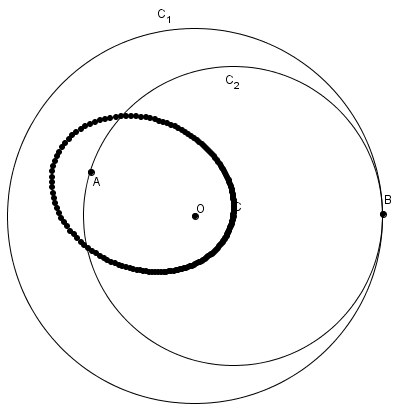
Cette propriété nous permet de réaliser la construction suivante. Sur un morceau de papier circulaire, identifier un point \(A\) autre que le centre. Pliez ensuite le morceau de papier de telle sorte qu’un point sur sa circonférence vienne coïncider avec le point \(A\). Dépliez et répétez avec différents points, tous issus de la circonférence. Tous ces pliages envelopperont une ellipse. Considérez le point \(B\) sur la circonférence. La seule façon de ramener \(B\) sur \(A\), deux points issus de la circonférence, est de plier selon le diamètre de \(C_{2}\). La pliure passe donc par \(C\). Qui plus est, la pliure est tangente à l’ellipse. Si la pliure n’était pas tangente, alors elle couperait l’ellipse en un deuxième point, par exemple \(C’\). Il faudrait alors que \(C’\) soit le centre d’un deuxième cercle tangent en \(B\) à \(C_{1}\) et passant par \(A\), une impossibilité !

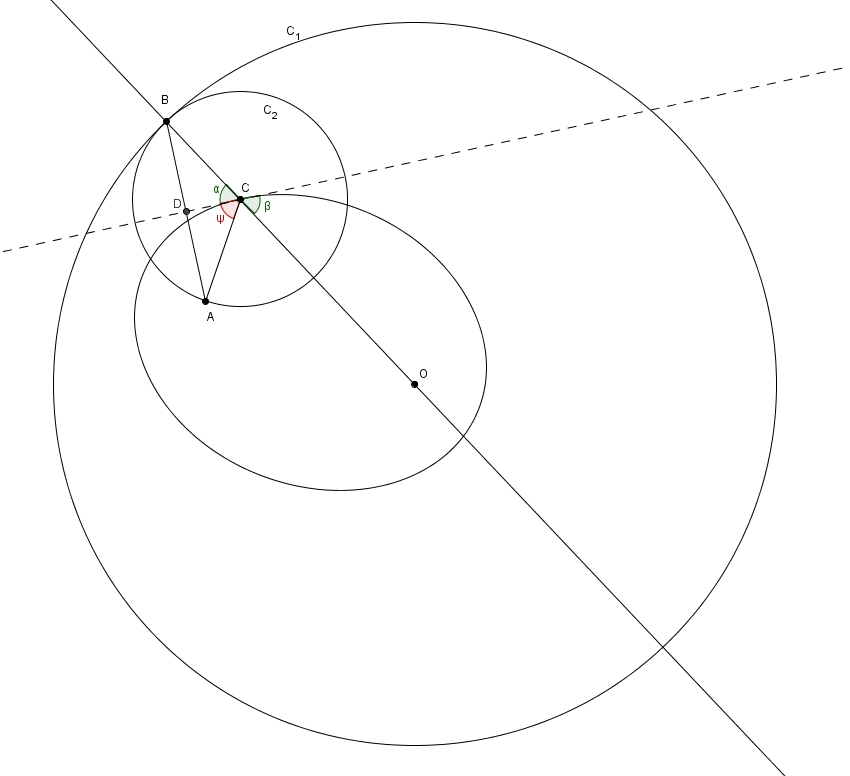
Par ailleurs, les triangles \(BCD\) et \(ACD\) sont isométriques (cas CCC). Puisque dans les triangles isométriques les angles homologues sont isométriques, on trouve \(\alpha=\psi\). Or les angles \(\alpha\) et \(\beta\) sont isométriques puisqu’ils sont opposés par le sommet. On a donc \(\psi = \beta\). C’est une propriété intéressante de l’ellipse. Les segments qui joignent les foyers à un point sur l’ellipse rencontrent la tangente en ce point avec le même angle. Un rayon lumineux qui passe par un foyer et qui est réfléchi sur l’ellipse passera aussi obligatoirement par l’autre foyer.

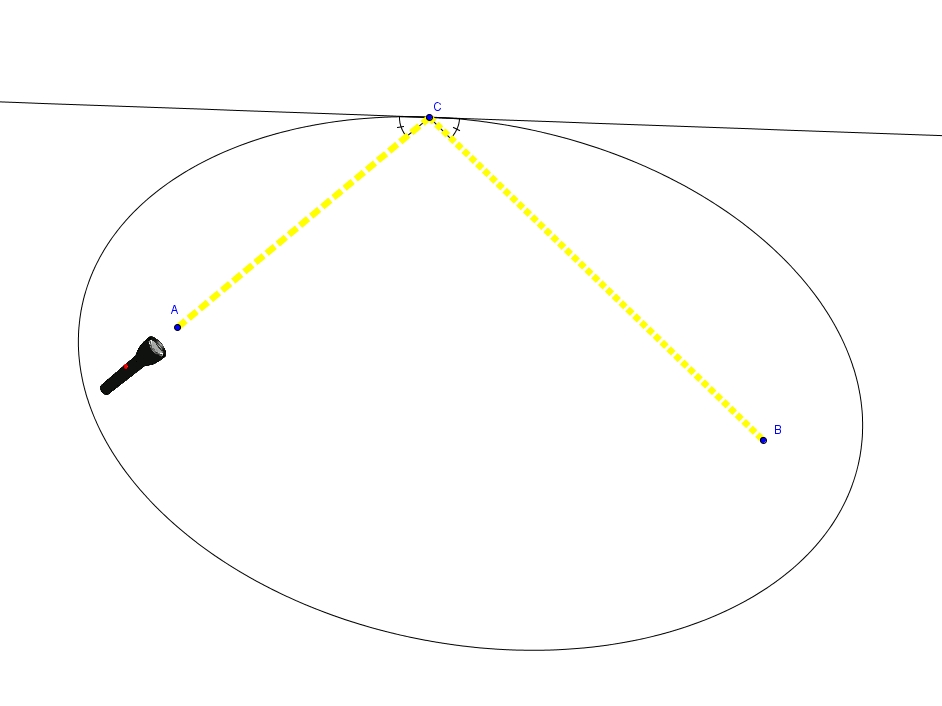
Référence : C. Stanley Ogilvy (1990), Excursions in Geometry

Le mathématicien arabe Al-Khawarizmi résout dans son livre paru en 825 et intitulé kitāb al-mukhtaṣar fī ḥisāb al-jabr wa’l-muqābalah (abrégé du calcul par la restauration et la comparaison) des équations du deuxième degré. Notez que le terme al-jabr du titre nous donnera plus tard le mot algèbre.

On peut résoudre ces équations, et faire la démonstration de la formule quadratique en « complétant le carré ». Voici donc une telle démonstration avec, en prime, et comme au temps d’Al-Khawarizmi, un support géométrique. On a donc \[ax^{2} + bx + c = 0\]On divise chaque terme par \(a\) \[x^{2}+\frac{b}{a}x+\frac{c}{a}=0\]et on complète le carré : c’est à dire rajouter une quantité qui fera en sorte que les trois premiers termes constituerons un trinôme carré parfait. Évidemment, il faut aussi retrancher immédiatement cette quantité afin de ne pas changer la valeur du polynôme. Quelle est cette quantité ? 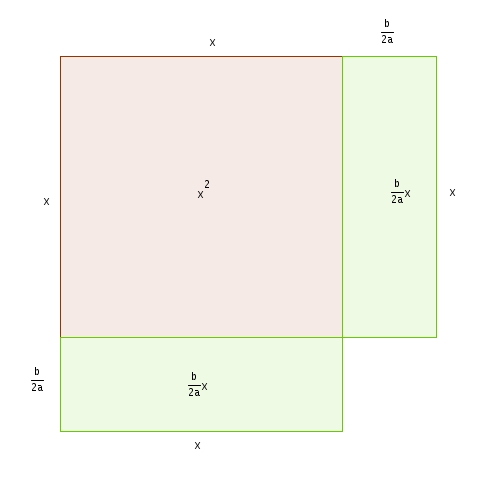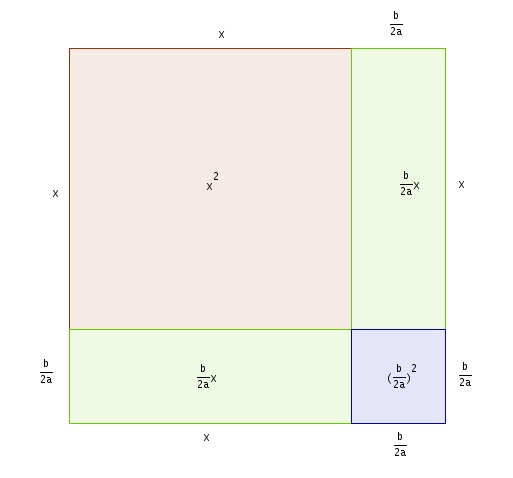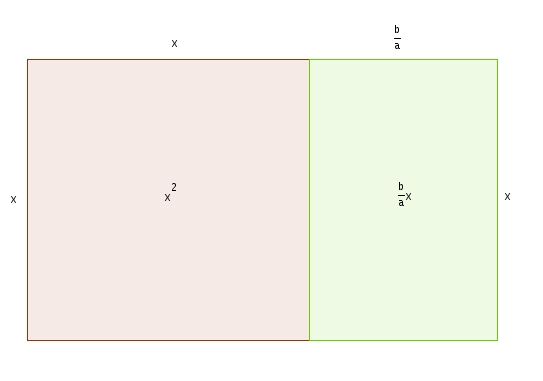Les deux premiers termes, étant ceux qui nous intéressent, sont représentés dans l’illustration suivante En séparant le rectangle vert en deux rectangle isométriques et en réarrangeant les pièces, on obtient

On se rend compte qu’il nous sera possible de compléter le carré faut en ajoutant \[\left(\frac{b}{2a}\right)^{2}\]tel qu’illustré dans le diagramme suivant

On se retrouve ainsi avec un carré dont les côtés mesurent \[x + \frac{b}{2a}\]Enfin bref, on a \[x^{2}+\frac{b}{a}x+\left(\frac{b}{2a}\right)^{2}-\left(\frac{b}{2a}\right)^{2}+\frac{c}{a}=0\]
ou \[x^{2}+\frac{b}{a}x + \frac{b^{2}}{4a^{2}}-\frac{b^{2}}{4a^{2}}+\frac{c}{a}=0\]Il est possible de factoriser le trinôme carré parfait \[\left(x+\frac{b}{2a}\right)^{2}-\frac{b^{2}}{4a^{2}}+\frac{c}{a}=0\]On isole ensuite le carré \[\left(x+\frac{b}{2a}\right)^{2}=\frac{b^{2}}{4a^{2}}-\frac{c}{a}\]On met ensuite les termes de droite sur dénominateur commun \[\left(x+\frac{b}{2a}\right)^{2}=\frac{b^{2}}{4a^{2}}-\frac{4ac}{4a^{2}}\]ce qui nous permet d’écrire \[\left(x+\frac{b}{2a}\right)^{2}=\frac{b^{2}-4ac}{4a^{2}}\]Il suffit maintenant d’extraire la racine carrée de chaque côté \[x+\frac{b}{2a}=\pm\sqrt{\frac{b^{2}-4ac}{4a^{2}}}\]Et là une propriétés des racines nous permet d’écrire ceci \[x+\frac{b}{2a}= \frac{\pm\sqrt{b^{2}-4ac}}{\sqrt{4a^{2}}}\]afin de simplifier comme cela\[x +\frac{b}{2a} = \frac{\pm\sqrt{b^{2}-4ac}}{2a}\]Il suffit enfin d’isoler \(x\) \[x=-\frac{b}{2a}\pm\frac{\sqrt{b^{2}-4ac}}{2a}\]ce qui fait \[x = \frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\]Le but de ce distrayant billet est de présenter une deuxième technique : le changement de variable. On sait que si notre équation ne comporte qu’un terme au carré, par exemple \[x^{2} = c\]on n’a qu’à extraire la racine carrée des deux côtés afin d’obtenir \[x = \pm \sqrt{c}\]soit les solutions de l’équation. C’est en quelque sorte une situation idéale. C’est donc le terme du premier degré qui cause problème. Il est possible d’éliminer ce terme avec un changement de variable. Nous avons donc à nouveau \[ax^{2}+bx + c = 0\]On divise ensuite chaque terme par \(a\) \[x^{2}+\frac{b}{a}x+\frac{c}{a} = 0\]Et là on effectue le changement de variable suivant \[x = y-\alpha\]ce qui fait \[\left(x-\alpha\right)^{2}+\frac{b}{a}\left(y-\alpha\right)+\frac{c}{a}=0\]En développant on obtient \[y^{2}-2\alpha y +\alpha^{2}+\frac{b}{a}y-\frac{b}{a}\alpha+\frac{c}{a}=0\]puis en regroupant les termes semblables \[y^{2}+\frac{b}{a}y-2\alpha y + \alpha^{2}-\frac{b}{a}\alpha+\frac{c}{a}=0\]La mise en évidence de \(y\) donne \[y^{2}+\left(\frac{b}{a}-2\alpha\right)y+\alpha^{2}-\frac{b}{a}\alpha+\frac{c}{a}=0\]L’objectif du changement de variable est d’éliminer le terme en \(y\). Posons\[\frac{b}{a}-2\alpha=0\]Il suffit d’isoler \(\alpha\) \[-2\alpha=-\frac{b}{a}\]puis \[\alpha = \frac{b}{2a}\]C’est cette valeur qui fera disparaître le terme du premier degré dans l’équation précédente. Remplaçons \[y^{2}+\left(\frac{b}{a}-2\left(\frac{b}{2a}\right)\right)y + \left(\frac{b}{2a}\right)^{2}-\frac{b}{a}\left(\frac{b}{2a}\right)+\frac{c}{a}=0\]En multipliant les parenthèses on obtient \[y^{2}+\left(\frac{b}{a}-\frac{2b}{2a}\right)y+\frac{b^{2}}{4a^{2}}-\frac{b^{2}}{2a^{2}}+\frac{c}{a}=0\]puis en simplifiant un peu \[y^{2}\left(\frac{b}{a}-\frac{b}{a}\right)y + \frac{b^{2}}{4a^{2}}-\frac{b^{2}}{2a^{2}}+\frac{c}{a}=0\]On obtient ce qui était attendu\[y^{2}+(0)y+\frac{b^{2}}{4a^{2}}-\frac{b^{2}}{2a^{2}}+\frac{c}{a}=0\]En mettant sur dénominateur commun \[y^{2}+\frac{b^{2}}{4a^{2}}-\frac{2b^{2}}{4a^{2}}+\frac{4ac}{4a^{2}}=0\]on obtient \[y^{2}+\frac{-b+4ac}{4a^{2}}=0\]Puis en isolant \(y^{2}\) \[y^{2}=\frac{b^{2}-4ac}{4a^{2}}\]et en extrayant la racine carrée de chaque côté de l’égalité \[y = \pm\sqrt{\frac{b^{2}-4ac}{4a^{2}}}\]Un propriété des racines nous permet d’écrire \[y = \frac{\pm\sqrt{b^{2}-4ac}}{\sqrt{4a^{2}}}\]puis de simplifier \[y = \frac{\pm\sqrt{b^{2}-4ac}}{2a}\]Or, on avait posé \[x = y-\alpha\]avec\[\alpha=\frac{b}{2a}\]En remplaçant on obtient \[x = y-\frac{b}{2a}\]et donc \[x+\frac{b}{2a}=y\]Il suffit maintenant de substituer \(y\) dans \[y = \frac{\pm\sqrt{b^{2}-4ac}}{2a}\]ce qui donne\[x+\frac{b}{2a}=\frac{\pm\sqrt{b^{2}-4ac}}{2a}\]et donc \[x=-\frac{b}{2a}\pm\frac{\sqrt{b^{2}-4ac}}{2a}\]Or comme les deux termes sont déjà sur dénominateur commun, on obtient finalement \[x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\]La méthode semble fastidieuse dans ce contexte relativement simple. Mais c’est cette méthode qui est utilisée dans la résolution d’un polynôme du troisième degré. Il est donc préférable d’en avoir pleine compréhension avant de se lancer dans l’entreprise éminemment plus complexe qu’est la résolution d’un polynôme du troisième degré.

Embrace your inner geekiness

C’est mon ami Monsieur C. qui m’a fait découvrir Wolfram | Alpha au moment de son lancement. Il l’utilisait entre autres pour calculer ses anniversaires de jours (incidemment, je viens tout juste de fêter mon 10000^ième anniversaire). J’ai découvert depuis qu’on pouvait faire pas mal plus “geek”. On peut célébrer nos anniversaires “premiers”.

Sur Wolfram | Alpha, entrez “days since [votre date de naissance]”. Pál Erdős, s’il était encore vivant, pourrait entrer :

On demande ensuite à Wolfram | Alpha la liste des nombres premiers aux alentours de 35594. On entre “prime numbers between […] and […]”.

M. Erdős célèbrerait donc plusieurs anniversaires « premiers» dans les prochains jours (mais n’aurait probablement pas besoin d’un outil comme Wolfram | Alpha pour les calculer). Si vous trouvez que les anniversaires « premiers » sont trop nombreux, vous pouvez ne célébrer que les anniversaires « premiers jumeaux ». M. Erdős célèbrerait ses prochains anniversaires « premiers jumeaux » à ses 35801^ième et 35803^ième jours de naissance soit…

les samedi 2 avril 2011 et lundi 4 avril 2011.  La conjecture des nombres premiers jumeaux affirme qu’il existe une infinité de ces nombres premiers \(p\) tels que \(p+2\) est aussi premier.  Erdős s’est intéressé à cette conjecture mais elle reste toujours à démontrer.  Si les nombres premiers jumeaux sont encore trop nombreux à votre goût, vous pouvez ne vous intéresser qu’aux nombres premiers qui sont aussi des palindromes.  On ne sait pas encore aujourd’hui s’il existe une infinité de ces nombres mais en voici quelques uns…

2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10301, 10501, 10601, 11311, 11411, 12421, 12721, 12821, 13331, 13831, 13931, 14341, 14741, 15451, 15551, 16061, 16361, 16561, 16661, 17471, 17971, 18181, 18481, 19391, 19891, 19991, 30103, 30203, 30403, 30703, 30803, 31013, 31513, 32323, 32423, 33533, 34543, 34843, 35053, 35153, 35353, 35753, 36263, 36563, 37273, 37573, 38083, 38183, 38783, 39293, 70207, 70507, 70607, 71317, 71917, 72227, 72727, 73037, 73237, 73637, 74047, 74747, 75557, 76367, 76667, 77377, 77477, 77977, 78487, 78787, 78887, 79397, 79697, 79997, 90709, 91019, 93139, 93239, 93739, 94049, 94349, 94649, 94849, 94949, 95959, 96269, 96469, 96769, 97379, 97579, 97879, 98389, 98689 …

 

Référence :http://travelsinamathematicalworld.blogspot.com/2010/08/prime-birthdays-via-wolframalpha.html via http://jd2718.wordpress.com/2010/09/03/carnival-of-mathematics-69/