Category: Mathématiques

J’adore le blogue Five Triangles (surtout les questions de géométrie) et j’en ai déjà parlé ici. Le sous-titre de ce blogue est unemasculated mathematics for school years 6, 7 & 8 ~ or thereabouts. Ainsi, malgré le réflexe d’utiliser l’artillerie lourde au premier abord (ça fonctionne après tout), il existe souvent (jusqu’à preuve du contraire) un moyen simple et ingénieux de s’en sortir. Dans les problèmes favoris des auteurs, on trouve

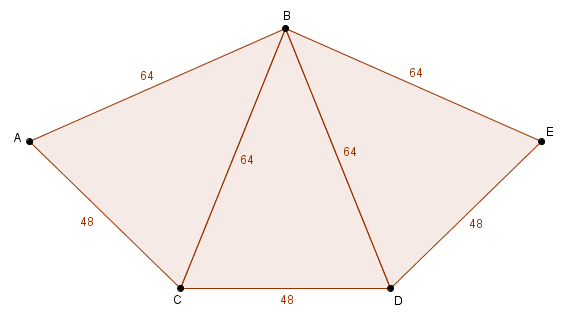
Le pentagone \(ABEDC\) ci-dessus est composé de trois triangles isocèles isométriques dont les côtés sont \(64\), \(64\) et \(48\). Quelle est la mesure du segment \(AE\) ?

En posant la mesure de l’angle \(ABC\) égale à \(\alpha\) 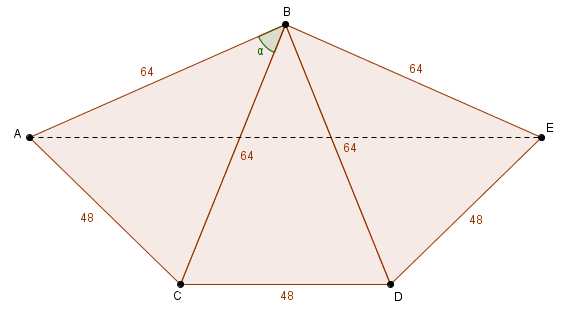on peut utiliser la loi des cosinus dans le triangle \(ABC\) \[48^{2}=64^{2}+64^{2}-2\cdot 64\cdot 64\cdot \cos(\alpha)\]En regroupant les termes constants et en simplifiant, on obtient\[\frac{-5\,888}{-8\,192}=\cos(\alpha)\]Hummm, la fraction réduite, \[\frac{23}{32} = \cos(\alpha)\]n’est pas une valeur remarquable pour le cosinus. Cela est un peu problématique car en utilisant la loi des cosinus dans le triangle \(ABE\), on obtient \[\left(m\overline{AE}\right)^{2} = 64^{2}+64^{2}-2\cdot 64 \cdot 64 \cdot \cos(3\alpha)\]ou \[\left(m\overline{AE}\right)^{2}=8\,192-8\,192\cos(3\alpha)\]et on doit trouver une valeur pour \(\cos(3\alpha)\) en fonction de celle de \(\cos(\alpha)\). Un peu fastidieux, mais encore, pas de problème ! En se rappelant les formules d’addition d’angles\[\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)\]et\[\sin(x+y) = \sin(x)\cos(y)+\sin(y)\cos(x)\]et en les appliquant deux fois, on peut obtenir une formule du cosinus de l’angle triple. Dans un premier temps, on obtient celle de l’angle double \begin{align*} \cos(2x)&=\cos(x+x) \\ \\ &=\cos(x)\cos(x)-\sin(x)\sin(x) \\ \\ &= \cos^{2}(x)-\sin^{2}(x)\end{align*}et comme \[\sin^{2}(x)=1-\cos^{2}(x)\]on peut remplacer et obtenir \begin{align*}\cos(2x)&=\cos^{2}(x)-\sin^{2}(x) \\ \\ &=\cos^{2}(x)-\left(1-\cos^{2}(x)\right) \\ \\ &=2\cos^{2}(x)-1\end{align*}Quant au sinus, on trouve pour l’angle double \begin{align*}\sin(2x)&=\sin(x+x)\\ \\ &=\sin(x)\cos(x) + \sin(x)\cos(x) \\ \\ &=2\sin(x)\cos(x)\end{align*}Enfin, en réutilisant la formule d’addition d’angles pour le cosinus, on obtient le cosinus de l’angle triple\begin{align*} \cos(3x) &=\cos(2x+x) \\ \\ &=\cos(2x)\cos(x)-\sin(2x)\sin(x) \\ \\ &=\left(2\cos^{2}(x)-1\right)\cos(x)-\left(2\sin(x)\cos(x)\right)\sin(x) \\ \\ &=2\cos^{3}(x)-\cos(x)-2\sin^{2}(x)\cos(x)\end{align*}En utilisant encore la substitution \[\sin^{2}(x)=1-\cos^{2}(x)\]on obtient \begin{align*}\cos(3x) &= 2\cos^{3}(x)-\cos(x)-2\sin^{2}(x)\cos(x)\\ \\ &=2\cos^{3}(x)-\cos(x)-2\left(1-\cos^{2}(x)\right)\cos(x) \\ \\ &=2\cos^{3}(x)-\cos(x)-2\cos(x)+2\cos^{3}(x) \\ \\ &=4\cos^{3}(x)-3\cos(x)\end{align*}En outre, \[\left(m\overline{AE}\right)^{2}=8\,192-8\,192\cos(3\alpha)\]devient\[\left(m\overline{AE}\right)^{2}=8\,192-8\,192\left(4\cos^{3}(\alpha)-3\cos(\alpha)\right)\]et puisque\[\cos(\alpha)=\frac{23}{32}\]on trouve \[\left(m\overline{AE}\right)^{2}=8\,192-8\,192\left(4\left(\frac{23}{32}\right)^{3}-3\left(\frac{23}{32}\right)\right)\]Un peu d’arithmétique nous donne\begin{align*}\left(m\overline{AE}\right)^{2}&=8\,192-8\,192\left(\frac{12\,167}{8\,192}-\frac{69}{32}\right) \\ \\ &= 8\,192 + 5\,497 \\ \\ &= 13\,689\end{align*}et on trouve, ô surprise, une mesure entière pour le segment \(AE\) \[m\overline{AE} = \sqrt{13\,689} = 117\]Bien sûr, c’est décevant. Un si beau nombre. Entier. Et une démarche si compliquée ! Peut-on faire plus simple ?

En plaçant la figure dans un plan cartésien, on peut ramener le problème à résoudre un système d’équations du deuxième degré.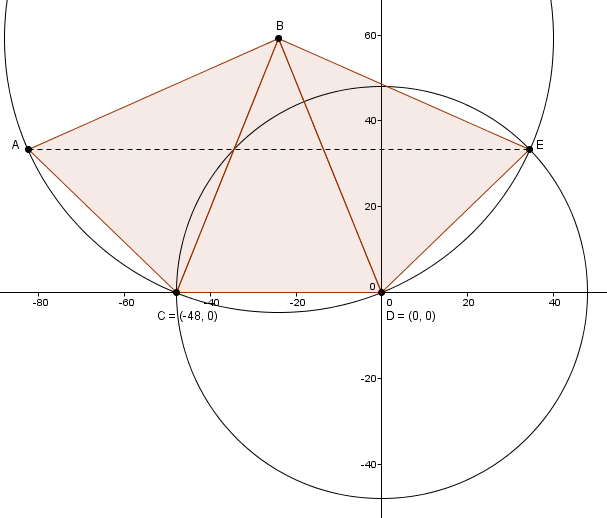
Avec Pythagore, on peut trouver l’ordonnée de \(B\) \begin{align*}\left(-24\right)^{2}+{y_{B}}^{2}&= 64^{2} \\ \\ 576 + {y_{B}}^{2}&=4\,096 \\ \\ {y_{B}}^{2}&=3\,520 \\ \\ y_{B}&=\pm 8\sqrt{55}\end{align*}et on garde la valeur positive. Les équations des cercles sont \begin{align*}x^{2}+y^{2}&=48^{2} \\ \\ \left(x+24\right)^{2}+\left(y+8\sqrt{55}\right)^{2}&=64^{2}\end{align*}On peut isoler \(y^{2}\) dans la première équation \[y^{2}=2\,304-x^{2}\]et substituer dans la deuxième \begin{align*}x^{2}+48x+576+y^{2}+16\sqrt{55}y+3\,520&=4\,096 \\ \\ x^{2}+48x+\left(2\,304-x^{2}\right)+16\sqrt{55}y&=0 \\ \\ 16\sqrt{55}y&=-\left(48x+2\,304\right)\end{align*}En divisant par \(16\), le facteur commun, \[\sqrt{55}y=-\left(3x+144\right)\]puis en élevant au carré et en substituant \(y^{2}\) à nouveau\begin{align*}55y^{2}&=9x^{2}-864x+20\,736 \\ \\ 55\left(2\,304-x^{2}\right) &= 9x^{2}-864x+20\,736 \\ \\ 126\,720-55x^{2}&=9x^{2}-864x+20\,736 \\ \\ 0&=64x^{2}-864x-105\,984\end{align*}En divisant par \(32\) on obtient \[0=2x^{2}+27x-3\,312\]On peut calculer le discriminant\begin{align*}\Delta &= 27^{2}-4\cdot 2 \cdot (-3\,312) \\ \\ &= 729 + 26\, 496 \\ \\ &=27\, 225\end{align*}Sans surprise \(27\,225\) est un carré (après tout, \(-48\) est une solution connue). Avec la formule quadratique, on obtient pour valeurs de \(x\) \[x = \frac{-27\pm\sqrt{27\, 225}}{2(2)}\]ou de manière équivalente\[x = \frac{-27\pm165}{4}\]Si la première solution est connue \[x_{1}= \frac{-27-165}{4}=-18\]la deuxième, elle, nous permet de répondre (à nouveau) à la question\[x_{2}=\frac{-27+165}{4}=\frac{69}{2}\]En effet, la distance entre \(A\) et \(E\) correspond à\[48+2\cdot \frac{69}{2}=117\]Plus élémentaire ? Peut-être. Plus simple ? C’est discutable. On pourrait faire un peu mieux, en calquant la deuxième démarche mais en évacuant le plan cartésien et les équations de cercles et en remplaçant le tout avec une grosse dose de Pythagore. Cela ferait plus school years 6, 7 & 8 ~ or thereabouts que les démarches précédentes, mais il me semble que la route est longue et aride.

Alors la question : quelle savante astuce nous permet de « voir » le \(117\) ?

Mise à jour :

Merci à Manuel qui, dans les commentaires, partage une solution vraiment simple !

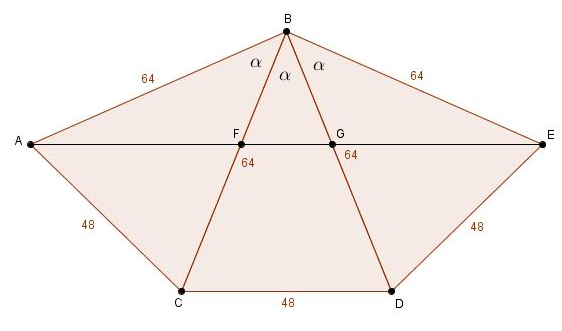
Dans le triangle isocèle \(ABC\), la mesure de l’angle \(ACB\) est \[\frac{180^{\circ}-\alpha}{2}\]Dans le triangle isocèle \(ABE\), la mesure de l’angle \(BAE\) est\[\frac{180^{\circ}-3\alpha}{2}\]Dans le triangle \(AFB\), la mesure de l’angle \(AFB\) est\[\frac{180^{\circ}+\alpha}{2}\]L’angle \(AFC\) et \(AFB\) étant adjacents supplémentaires, la mesure de l’angle \(AFC\) est\[\frac{180^{\circ}-\alpha}{2}\]Le triangle \(ACF\) est donc isocèle et pour reprendre l’explication de Manuel,

\(m\overline{AF} = 48\) et le triangle \(ACF\) est semblable à \(ABC\) avec un coefficient de proportionnalité de \(\frac{9}{16}\), d’où \(m\overline{CF} = 36\) et, par Thalès, dans \(\triangle ACD\), \(m\overline{FG} = 21\).
Donc \(m\overline{AE} = 48 + 21 + 48 = 117\).

Je partage cette petite trouvaille rencontrée en élaborant un exercice pour mes élèves sur la droite d’Euler : il s’agit d’un triangle scalène, non rectangle, dans lequel les trois sommets (\(A\), \(B\), \(C\)), les trois pieds des hauteurs (\(H_{1}\), \(H_{2}\), \(H_{3}\)), les trois points milieux des côtés (\(M_{1}\), \(M_{2}\), \(M_{3}\)) et les points d’intersection des médianes (\(M_{0}\)), médiatrices (\(R_{0}\)) et hauteurs (\(H_{0}\)) ont tous des coordonnées entières et dont les côtés ne sont pas parallèles aux axes. Qui plus est, les pieds des hauteurs tombent sur les côtés (et non sur leurs prolongements) et les trois points d’intersection se trouvent à l’intérieur du triangle.

Sur la figure, le triangle, en bleu, les médianes tracées avec des traits pointillés fins, les hauteurs avec des traits pointillés longs, et les médiatrices avec des traits continus. La droite d’Euler est en rouge.

Si on laisse tomber la condition que les points d’intersections \(H_{0}\), \(R_{0}\) et \(M_{0}\) soient à l’intérieur du triangle, on peut trouver facilement des triangles beaucoup plus petits (il en existe beaucoup), par exemple celui-ci

Bon. Je suis loin d’avoir fait une recherche exhaustive, mais voilà : je doute qu’il existe des triangles beaucoup plus petits que celui ci-dessus. Si vous en trouvez, s’il vous plait, faites-moi en part !

En ce qui me concerne, après tâtonnements dans Géogébra, j’ai cru bon partir du point d’intersection des médiatrices, équidistant des trois sommets, et de reconstruire les sommets du triangle à partir de là. Pour éviter d’obtenir des triangles rectangles (\(R_{0}\) tombe sur l’hypoténuse) ou isocèles, ou des côtés parallèles aux axes, j’ai utilisé pour les accroissements le plus petit nombre exprimable comme somme de deux carrés de trois façons différentes : \[325 = 1^{2}+18^{2}=66^{2}+17^{2}=10^{2}+15^{2}\]Après un peu de jonglerie avec les combinaisons possibles de ces nombres, j’ai ensuite redimensionné le triangle afin que tous les points mentionnés ci-haut soient à coordonnées entières (en multipliant les accroissements par le PPCM des dénominateurs des coordonnées rationnelles). Je n’ai aucune idée cependant si cette démarche est la meilleure !

Vous résolvez des équations avec des racines carrées et vos élèves sont troublés lorsqu’ils élèvent au carré et insèrent peut-être par le fait même une ou des fausses solutions à l’équation initiale ? Par exemple, pour résoudre \[\sqrt{x + 3} = x+1\]on élève au carré pour se débarrasser de la racine carrée à gauche \[x + 3 = \left(x+1\right)^{2}\]On développe \[x + 3 = x^{2}+2x+1\]On regroupe \[0 = x^{2} + x-2\]et on factorise \[0 = (x+2)(x-1)\]Les solutions à la dernière équations sont \(-2\) et \(1\). Si \(1\) est bien une solution de l’équation initiale \begin{align*}\sqrt{1+3} &= 1+1 \\ \\ \sqrt{4}&=2 \\ \\ 2&=2\end{align*}on ne peut pas en dire autant de \(-2\) \begin{align*}\sqrt{-2+3} &\neq -2+1 \\ \\ \sqrt{1}&\neq -1 \\ \\ 1 &\neq -1\end{align*}Lorsqu’on a élevé au carré, une fausse solution, \(-2\), s’est insérée. Calamité !

Exemple extrêêêêêêême

L’intrigue se corse. On veut résoudre\[\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=1\]une expression aux allures certainement plus menaçantes. On cherchera néanmoins à éliminer les racines. En élevant au carré on obtient \[x+3-4\sqrt{x-1}+2\sqrt{\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right)}+x+8-6\sqrt{x-1}=1\]qu’on simplifie en regroupant les termes semblables \[2x+11-10\sqrt{x-1}+2\sqrt{\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right)}=1\]ou de manière équivalente \[2\sqrt{\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right)}=10\sqrt{x-1}-2x-10\]En divisant par \(2\) \[\sqrt{\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right)} = 5\sqrt{x-1}-x-5\]et en élevant au carré pour se débarrasser de la racine à gauche, on obtient \begin{align*}\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right) &= \\ 25x-25-5x\sqrt{x-1}-25\sqrt{x-1}&-5x\sqrt{x-1}+x^{2}+5x-25\sqrt{x-1}+5x+25\end{align*}ou en regroupant les termes semblables \[\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right)=x^{2}-10x\sqrt{x-1}+35x-50\sqrt{x-1}\]Dans l’espoir de regrouper les racines de \(x-1\), on développe le produit à gauche \begin{align*}x^{2}+8x-6x\sqrt{x-1}+3x+24-18\sqrt{x-1}-4x\sqrt{x-1}-32\sqrt{x-1}+24x+24 &= \\ x^{2}-10x\sqrt{x-1}+35x-50&\sqrt{x-1}\end{align*}puis on regroupe les termes semblables à gauche, \[x^{2}-10x\sqrt{x-1}+35x-50\sqrt{x-1}=x^{2}-10x\sqrt{x-1}+35x-50\sqrt{x-1}\]et là, ô surprise, une identité ! Vraie pour tout \(x\) ? On a élevé au carré, certes, mais on ne fait quand même pas dans la sorcellerie ! Une identité ! Que s’est-il passé ?

La clé de l’énigme consiste à remarquer que \begin{align*}x+3-4\sqrt{x-1}&=x-1-4\sqrt{x-1}+4 \\ \\ &=\left(\sqrt{x-1}-2\right)^{2}\end{align*}et\begin{align*}x+8-6\sqrt{x-1}&=x-1-6\sqrt{x-1}+9 \\ \\ &=\left(\sqrt{x-1}-3\right)^{2}\end{align*}c’est à dire que l’équation initiale est équivalente à \[\sqrt{\left(\sqrt{x-1}-2\right)^{2}}+\sqrt{\left(\sqrt{x-1}-3\right)^{2}}=1\]ou, exprimée avec des valeurs absolues, à \[\left|\sqrt{x-1}-2\right| + \left|\sqrt{x-1}-3\right| =1\]Maintenant, pour des valeurs de \(x\) telles que\[1\leq x \leq 5\]l’expression \[\sqrt{x-1}-2\]est négative et pour des valeurs de \(x\) telles que \[5\leq x\]l’expression \[\sqrt{x-1}-2\]est positive. D’autre part, pour des valeurs de \(x\) telles que \[1\leq x \leq 10\]l’expression \[\sqrt{x-1}-3\]est négative et pour des valeurs de \(x\) telles que\[10\leq x\]l’expression \[\sqrt{x-1}-3\]est positive. Ainsi, il y a trois cas à traiter. D’abord si \[1\leq x \leq 5\]les deux expressions sont négatives et pour se débarrasser des valeurs absolues on pose \[-\left(\sqrt{x-1}-2\right)-\left(\sqrt{x-1}-3\right) =1\]ce qui fait \[-2\sqrt{x-1}=-4\]puis en divisant par \(-2\) \[\sqrt{x-1}=2\]On trouve ainsi la solution \begin{align*}x-1&=4 \\ \\ x&=5\end{align*}et comme \[5\leq 5\]on accepte cette solution. Le deuxième cas à traiter est \[5\leq x \leq 10\]Dans ce cas, la première expression est positive mais la deuxième est négative. Pour enlever les valeurs absolues, on pose \[\sqrt{x-1}-2-\left(\sqrt{x-1}-3\right)=1\]ce qui fait \[\sqrt{x-1}-2-\sqrt{x-1}+3=1\]ou, ô surprise, \[1=1\]une identité ! C’est donc dire que cet intervalle au complet \[5 \leq x \leq 10\]est aussi solution à l’équation. Enfin, le troisième et dernier cas à considérer est \[10\leq x\]Dans ce cas, les deux expressions sont positives et donc on a \[\sqrt{x-1}-2+\sqrt{x-1}-3=1\]ce qui fait \[2\sqrt{x-1}=6\]puis en divisant par \(2\) \[\sqrt{x-1}=3\]et là on trouve la solution \begin{align*}x-1&=9 \\ \\ x&= 10\end{align*}Et comme\[10\leq10\]on accepte cette solution.

L’ensemble solution à l’équation initiale comprend donc tout l’intervalle fermé \(\left[5,\, 10\right]\) et comporte ainsi une infinité de solutions. Du coup, la stratégie d’élever au carré pour éliminer les racines produit un polynôme qui comporte au moins autant de solutions que l’équation initiale, c’est-à-dire une infinité, et on obtient ainsi une identité.

Références : Edward J. Barbeau (2013), More Fallacies, Flaws and Flimflam