Category: Mathématiques

 

XKCD : A webcomic of romance, sarcasm, math, and language.

S’il s’est écoulé pas mal de temps avant que j’écrive un nouveau billet, c’est qu’un petit problème génial a occupé une grande partie de mon temps libre.  En effet, il se trouve qu’un de mes collègues a une passion pour les mathématiques toute aussi forte que la mienne.  Voici le problème qu’il m’a envoyé la semaine dernière.  Un problème simple (et connu) mais dont la solution s’avère, on s’en doute, plutôt ardue.  Il s’agit de compter le nombre de triangles équilatéraux que l’on retrouve dans un grand triangle équilatéral de côté \(n\).

Pour \(n=1\)

\(n=2\)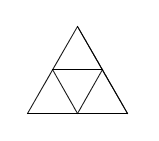\(n=3\)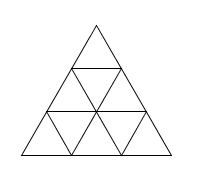\(n=4\)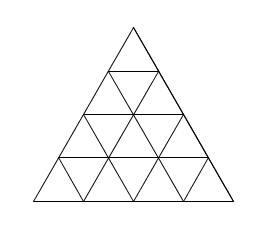\(n=5\)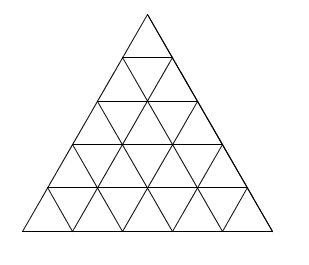\(n=6\)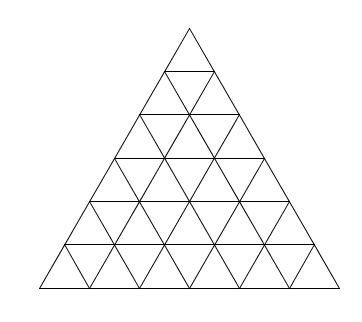Et comme je n’ai trouvé nulle part sur Internet les images des triangles pour les valeurs de \(n\) subséquentes, et que de tracer ces triangles à la main est une tâche plutôt ingrate, et que si vous êtes comme moi vous voudrez sûrement dénombrer vous aussi, on a pour \(n=7\)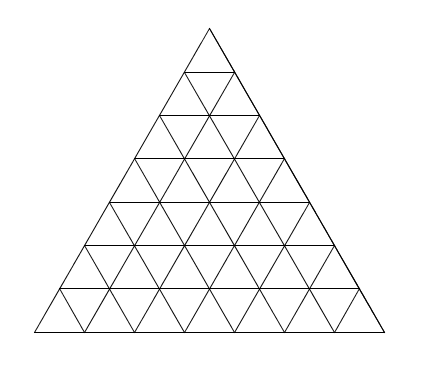\(n=8\)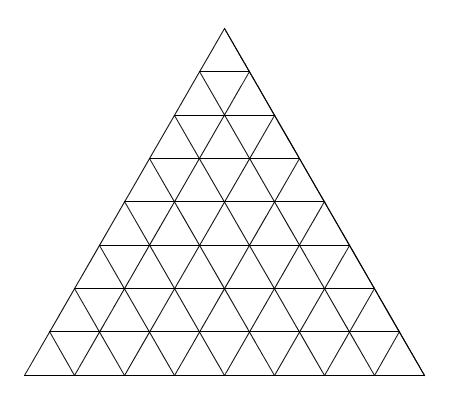\(n=9\)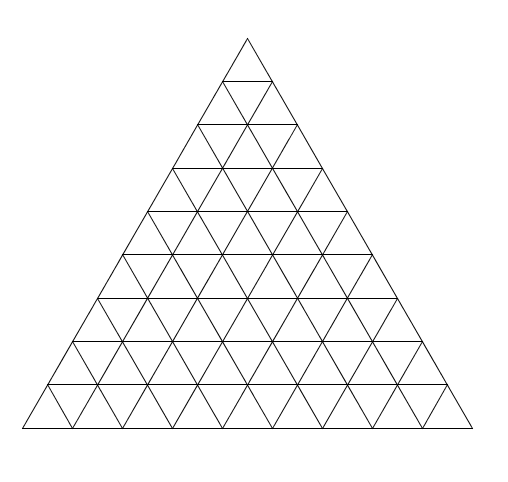et enfin \(n=10\)Non sans effort, vous trouverez peut-être ces résultats :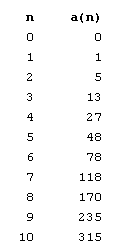

où \(a(n)\) est le nombre de triangles dans chaque figure.  Ce qui me frappe d’abord et avant tout c’est… qu’il n’y a effectivement rien de frappant dans les nombres de la colonne de droite.  On ne semble déceler aucune régularité évidente (outre que le nombre de petits triangles d’une unité de côté est toujours égal à \(n^{2}\)).  Il faut donc chercher plus loin.  On remarque, lors du dénombrement, qu’il y a quelque chose qui s’avère différent si le nombre \(n\) est pair ou impair.  Mais il ne s’agit, à cette étape-ci, que d’une conjecture.  D’ailleurs, en ne considérant dans le tableau précédent que les valeurs de \(n\) paires (ou impaires), on peut constater que les accroissements entre les accroissements entre les accroissements sont constants (vous trouverez que les accroissements entre les accroissements entre les accroissements valent tous \(12\)).  On peut donc espérer pour l’instant que la ou les règles recherchées soient des polynômes du troisième degré.

Lorsqu’on compte le nombre de triangles, on tient compte du nombre de triangles des différentes grosseurs.  Par exemple, en considérant \(n=5\)

on s’aperçoit qu’il contient \(25\) petits triangles de une unité de côté.  Il contient aussi \(13\) plus grands triangles de \(2\) unités de côté (ou composés de \(4\) petits triangles).  Il contient \(6\) triangles encore plus grands de \(3\) unités de côté (ou composés de \(9\) petits triangles).  Il contient \(3\) grands triangles de quatre unités de côté (ou composés de \(16\) petits triangles) et finalement \(1\) triangle de \(5\) unités de côté (ou composé de \(25\) petits triangles).  On obtient bien \[25 + 13 + 6 + 3 + 1 = 48\]Non sans effort, vous pourrez construire le tableau suivant pour les premières valeurs de \(n\) (en comptant séparément les plus petits triangles de côté \(k\)) :

Et pourtant, encore une fois, aucune régularité ne semble transparaître (enfin pour moi…)  J’ai soumis ce problème à mes élèves (pour leur montrer qu’un problème simple peut avoir une solution loin d’être triviale) et un de ceux-ci est venu me voir avec ses calculs.  Il avait fait un tableau semblable au miens mais n’avait compté (par mégarde) que les triangles « à l’endroit », c’est-à-dire ceux qui pointent vers le haut. Ah! Erreur d’un élève ? Nouvelle piste ? Il s’avère que décomposer le problème en un problème de « nombre triangles pointant vers le haut » et « nombre triangles pointant vers le bas » (plutôt que « nombre de triangles de \(k\) unités de côté »)  s’avère drôlement fructueux.

Le tableau précédant devient plutôt

Nous allons définir la fonction a comme suit : \[a(n) = u(n) + v(n)\]dans laquelle \(u\) donne le nombre de triangles pointant vers le haut et \(v\) le nombre de triangles pointant vers le bas.

Considérons le petit triangle de côté \(k\) pointant vers le haut dans ce triangle de côté \(n\).

Le sommet du triangle de côté \(k\) doit obligatoirement être dans la région rougeâtre sur le schéma.  Il y a donc un seul triangle à partir du haut, deux sur l’étage immédiatement inférieur, trois sur le suivant et ce jusqu’à au dernier étage.  Mais, justement, combien y a-t-il de ces triangles au dernier étage ? En comptant bien, on trouve \[n-k+1\]triangles possibles.  Pour un \(k\) et un \(n\)  donnés, il y a donc \[1 + 2 + 3 + 4 + 5+ \ \dots \ + (n-k+1)\]triangles, ce qui se somme à \[\frac{(n-k+1)(n-k+1+1)}{2}\]ou plus simplement \[\frac{(n-k+1)(n-k+2)}{2}\]Maintenant, quelle est la valeur maximale de \(k\) ? Bien sûr, c’est \(n\).  On obtient donc \[u(n) = \sum_{k=1}^{n}\frac{(n-k+1)(n-k+2)}{2}\]ce qui fait en développant \[u(n) = \sum_{k=1}^{n}\frac{n^{2}+3n + 2 + k^{2}-2kn -3k}{2}\]puis en sortant le facteur \(\frac{1}{2}\) de la sommation \[u(n) = \frac{1}{2}\sum_{k=1}^{n}n^{2}+3n + 2 + k^{2}-2kn-3k\]On obtient dans un premier temps \[u(n) = \frac{1}{2}\left(n^{3}+3n^{2}+2n + \sum_{k=1}^{n}k^{2}-2n\sum_{k=1}^{n}k-3\sum_{k=1}^{n}k\right)\]puis, en se rappelant ceci, on obtient dans un deuxième temps \[u(n) = \frac{1}{2}\left(n^{3}+3n^{2}+2n + \frac{n(n+1)(2n+1)}{6}-2n\left(\frac{n(n+1)}{2}\right)-3\left(\frac{n(n+1)}{2}\right)\right)\]Suivent ces quelques étapes dans lesquelles on simplifie le tout.  D’abord \[u(n) = \frac{1}{2}\left(n^{3}+3n^{2}+2n +\frac{n(n+1)(2n+1)}{6}-n^{3}-n^{2}-\frac{3n^{2}}{2}-\frac{3n}{2}\right)\]puis \[u(n) = n^{2}+n + \frac{n(n+1)(2n+1)}{12}-\frac{3n^{2}}{4}-\frac{3n}{4}\]En mettant sur dénominateur commun \[u(n) = \frac{12n^{2}}{12}+\frac{12n}{12} + \frac{n(n+1)(2n+1)}{12}-\frac{9n^{2}}{12}-\frac{9n}{12}\]et en développant \[u(n) = \frac{12n^{2}+12n + 2n^{3}+3n^{2}+n-9n^{2}-9n}{12}\]on obtient \[u(n)=\frac{2n^{3}+6n^{4}+4n}{12}\]et finalement en divisant les numérateur et dénominateur par \(2\) \[u(n) = \frac{n^{3}+3n^{2}+2n}{6}\]Voilà donc l’expression qui nous donne le nombre de triangle pointant vers le haut.  Il reste à trouver \(v(n)\) On considère le petit triangle de côté \(k\) pointant vers le bas dans ce triangle de côté \(n\).

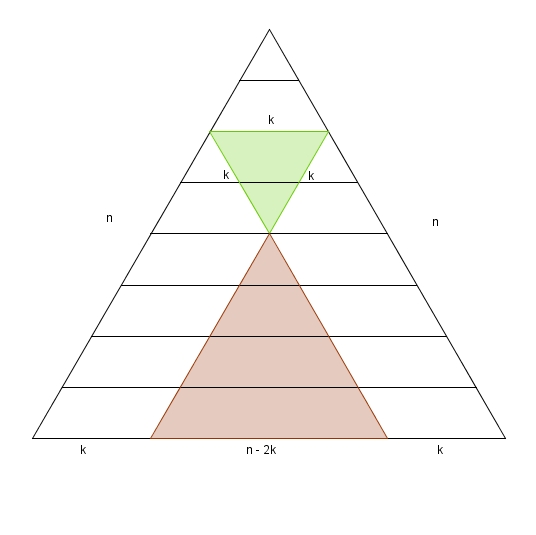Encore une fois, le sommet du triangle de k unités de côté doit obligatoirement se trouver dans la région rougeâtre sur le schéma.  Et, encore une fois, il y a un triangle possible à partir du haut, deux sur l’étage suivant, trois sur celui qui suit, et ce jusqu’au dernier étage.  Ici, au dernier étage, il y aura toujours \[n-2k+1\]triangles possibles.  Cela signifie que pour un \(k\) et un \(n\) donnés, il y aura donc \[1+2+3+4+ \ \dots \ +(n-2k+1)\]triangles, ce qui se somme à \[\frac{(n-2k+1)(n-2k+1+1)}{2}\]ou plus simplement\[\frac{(n-2k+1)(n-2k+2)}{2}\]Maintenant, quelle est la valeur maximale de \(k\) ? Dans le cas d’un \(n\) pair, il est facile de voir que ce sera \(\frac{n}{2}\).  Dans le cas d’un \(n\) impair, ce sera plutôt \(\frac{n-1}{2}\).  Voilà où se trouvait la différence entre les \(n\) pairs et impairs pressentie à l’étape préliminaire du dénombrement.

Pour une valeur de \(n\) paire

On trouve : \[v(n) = \sum_{k=1}^{\frac{n}{2}}\frac{(n-2k+1)(n-2k+2)}{2}\]ce qui fait en sortant le facteur \(\frac{1}{2}\) de la sommation \[v(u) = \frac{1}{2}\sum_{k=1}^{\frac{n}{2}}(n-2k+1)(n-2k+2)\]et en développant \[v(n) = \frac{1}{2}\sum_{k=1}^{\frac{n}{2}}n^{2}+3n+2+4k^{2}-4kn-6k\]On obtient alors dans un premier temps \[u(n) = \frac{1}{2}\left(\frac{n^{3}}{2}+\frac{3n^{2}}{2}+\frac{2n}{2}+4\sum_{k=1}^{\frac{n}{2}}k^{2}-4n\sum_{k=1}^{\frac{n}{2}}k-6\sum_{k=1}^{\frac{n}{2}}k\right)\] puis \[v(n) = \frac{1}{2}\left(\frac{n^{3}}{2}+\frac{3n^{2}}{2}+\frac{2n}{2}+4\cdot \frac{\frac{n}{2}\left(\frac{n}{2}+1\right)\left(2 \cdot \frac{n}{2} + 1\right)}{6}-4n\cdot \frac{\frac{n}{2}\left(\frac{n}{2}+1\right)}{2}-6\cdot\frac{\frac{n}{2}\left(\frac{n}{2}+1\right)}{2}\right)\]En développant davantage et simplifiant un peu on obtient \[v(n) = \frac{n^{3}}{4}+\frac{3n^{2}}{4}+\frac{2n}{4}+\frac{n^{3}+3n^{2}+2n}{12}-\frac{n^{3}+2n^{2}}{4}-\frac{3n^{2}+6n}{8}\]ce qui fait \[v(n) = \frac{n^{3}}{4}+\frac{3n^{2}}{4}+\frac{2n}{4}+\frac{n^{3}}{12}+\frac{3n^{2}}{12}+\frac{2n}{12}-\frac{n^{3}}{4}-\frac{2n^{2}}{4}-\frac{3n^{2}}{8}-\frac{6n}{8}\]En mettant sur dénominateur commun \[v(n) = \frac{6n^{3}}{24}+\frac{18n^{2}}{24}+\frac{12n}{24}+\frac{2n^{3}}{24}+\frac{6n^{2}}{24}+\frac{4n}{24}-\frac{6n^{3}}{24}-\frac{12n^{2}}{24}-\frac{9n^{2}}{24}-\frac{18n}{24}\]et en regroupant les termes semblables on trouve finalement \[v(n) = \frac{2n^{3}+3n^{2}-2n}{24}\]Cette expression nous donne le nombre de triangles pointant vers le bas pour un \(n\) pair.

Pour une valeur de \(n\) impaire

Dans ce cas, on aurait plutôt \[v(n) = \sum_{k=1}^{\frac{n-1}{2}}\frac{(n-2k+1)(n-2k+2)}{2}\]ce qui fait en sortant le facteur \(\frac{1}{2}\) de la sommation \[v(n) = \frac{1}{2}\sum_{k=1}^{\frac{n-1}{2}}(n-2k+1)(n-2k+2)\]et en développant \[v(n) = \frac{1}{2}\sum_{k=1}^{\frac{n-1}{2}}n^{2}+3n+2+4k^{2}-4kn-6k\]Dans un premier temps, on a \[v(n) = \frac{1}{2}\left(\frac{(n-1)(n^{2})}{2}+\frac{(n-1)(3n)}{2}+\frac{(n-1)(2)}{2}+4\sum_{k=1}^{\frac{n-1}{2}}k^{2}-4n\sum_{k=1}^{\frac{n-1}{2}}k-6\sum_{k=1}^{\frac{n-1}{2}}k\right)\]et dans un deuxième \[v(n) = \frac{1}{2}\left(\frac{n^{3}-n^{2}}{2}+\frac{3n^{2}-3n}{2}+\frac{2n-2}{2}+4\cdot \frac{\frac{n-1}{2}\left(\frac{n-1}{2}+1\right)\left(2\cdot \frac{n-1}{2}+1\right)}{6}-4n\cdot \frac{\frac{n-1}{2}\left(\frac{n-1}{2}+1\right)}{2}-6\cdot \frac{\frac{n-1}{2}\left(\frac{n-1}{2}+1\right)}{2}\right)\]En développant davantage et simplifiant un peu, on obtient \[v(n) = \frac{n^{3}-n^{2}}{4}+\frac{3n^{2}-3n}{4}+\frac{2n-2}{4}+\frac{n^{3}-n}{12}-\frac{n^{3}-n}{4}-\frac{3n^{2}-3}{8}\]puis \[v(n) = \frac{n^{3}}{4}-\frac{n^{2}}{4}+\frac{3n^{2}}{4}-\frac{3n}{4}+\frac{2n}{4}-\frac{2}{4}+\frac{n^{3}}{12}-\frac{n}{12}-\frac{n^{3}}{4}+\frac{n}{4}-\frac{3n^{2}}{8}+\frac{3}{8}\]en mettant sur dénominateur commun \[v(n) = \frac{6n^{3}}{24}-\frac{6n^{2}}{24}+\frac{18n^{2}}{24}-\frac{18n}{24}+\frac{12n}{24}-\frac{12}{24}+\frac{2n^{3}}{24}-\frac{2n}{24}-\frac{6n^{3}}{24}+\frac{6n}{24}-\frac{9n^{2}}{24}+\frac{9}{24}\]et en regroupant les termes semblables \[v(n) = \frac{2n^{3}+3n^{2}-2n-3}{24}\]Voilà ! Cette expression nous donne le nombre de triangles pointant vers le bas pour un \(n\) impair.

Le nombre de triangles au total

Il suffit maintenant de combiner ces résultats afin d’obtenir \(a(n)\). On a \[a(n) = u(n) + v(n)\]Dans le cas d’un \(n\) pair, on obtient \[a(n) = \frac{n^{3}+3n^{2}+2n}{6}+\frac{2n^{3}+3n^{2}-2n}{24}\]ce qui fait, en mettant sur dénominateur commun \[a(n) = \frac{4n^{3}+12n^{2}+8n}{24}+\frac{2n^{3}+3n^{2}-2n}{24}\]puis en regroupant les termes semblables \[a(n) = \frac{6n^{3}+15n^{2}+6n}{24}\]Finalement en divisant par \(3\) en haut et en bas, on obtient \[a(n) = \frac{2n^{3}+5n^{2}+2n}{8}\]toujours pour un \(n\) pair. Pour un \(n\) impair on a plutôt \[a(n) = \frac{n^{3}+3n^{2}+2n}{6} + \frac{2n^{3}+3n^{2}-2n-3}{24}\]ce qui fait, en mettant sur dénominateur commun \[a(n) = \frac{4n^{3}+12n^{2}+8n}{24}+\frac{2n^{3}+3n^{2}-2n-3}{24}\]puis en regroupant les termes semblables \[a(n) = \frac{6n^{3}+15n^{2}+6n-3}{24}\]Finalement, en divisant par \(3\) en haut et en bas, on obtient \[a(n) = \frac{2n^{3}+5n^{2}+2n-1}{8}\]pour un \(n\) impair.

Référence : http://mathforum.org/library/drmath/view/54369.html (En résolution de problèmes, il faut parfois étudier un problème connexe moins complexe pour avancer).

Voici une méthode pour trisecter un segment.  Il en existe plusieurs, et même des méthodes requérant moins d’étapes mais voici probablement la plus connue.  Ce qui nous est donné : le segment \(AB\).

On trace le cercle de centre \(A\) et de rayon \(\overline{AB}\).  On trace ensuite le cercle de centre \(B\) et et de rayon \(\overline{AB}\).  Ces deux cercles se croisent à deux endroits : appelons-les \(C\) et \(D\).  Traçons le cercle de centre \(C\) et de rayon \(\overline{AC}\).  Notons au passage que ce cercle passe aussi par \(B\) et que\[m\overline{AC}=m\overline{AB}\](c”est la méthode de construction d’un triangle équilatéral, Proposition 1 du Livre 1 des Éléments d’Euclide).  On trace ensuite la droite \(AC\) qui coupe le cercle de centre \(C\) en \(A\) (évidemment) mais aussi en \(E\).  On trace la droite \(DE\).  Cette dernière coupe \(\overline{AB}\) en \(F\).  Voilà !  On a \[m\overline{BF}=\frac{1}{3}m\overline{AF}\]

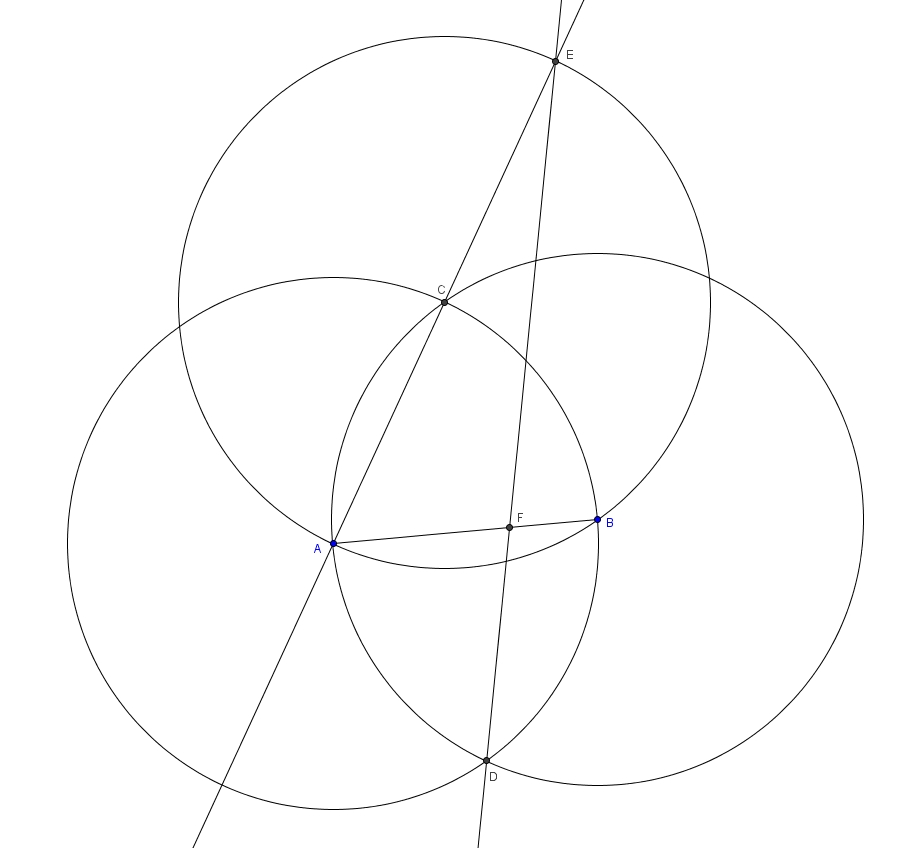Notons d’abord que les trois cercles sont isométriques puisque la mesure de leur rayon est égale à la mesure du segment \(AB\).  Considérons les triangles \(ABC\) et \(ABD\).  Ce sont des triangles équilatéraux (chacun de leurs côtés est, justement, un rayon des trois cercles congrus).  Les angles intérieurs d’un triangle équilatéral sont tous de \(60^{\circ}\).  En particulier, les angles \(BAC\) et \(ABD\) valent tous les deux \(60^{\circ}\). \[m\angle BAC = m\angle ABD = 60^{\circ}\]

***Ici, Grasyop remarque qu’il existe une façon plus élégante d’établir la congruence des angles \(BAC\) et \(BAD\).  On considère le losange \(ACBD\) (tous ses côtés ont pour mesure le rayon \(AB\)).  Les côtés opposés d’un losange étant parallèles, on trouve que les angles \(BAC\) et \(ABD\) sont des angles alternes-internes isométriques. *** Les angles \(AFE\) et \(BFD\) sont eux aussi  isométriques puisqu’ils sont opposés par le sommet.  Les triangles \(AEF\) et \(BDF\) sont donc semblables par le cas de similitude AA.

Et comme dans des triangles semblables les côtés homologues sont dans le même rapport, on déduit ceci : la mesure de \(\overline{AE}\) étant égale à deux rayons et la mesure de \(\overline{BD}\) à un rayon, le rapport de similitude est \(2\).  Et comme ce rapport est \(2\), cela implique que la mesure de \(\overline{AF}\) vaut deux fois celle de \(\overline{FB}\).  Et si \(\overline{AF}\) est effectivement deux fois plus grand que \(\overline{FB}\), alors on trouve que la mesure de \(\overline{AB}\) est vaut trois fois celle de \(\overline{FB}\).   C’est la trisection recherchée.