Voici une question qui m’a été posée par une élève récemment. Je n’ai pas la source de l’exercice.
Quelles sont les solutions à l’équation suivante : \[\left(x^{2}-5x + 5\right)^{x^{2}-9x+20} = 1\]
C’est un bon exercice sur les lois et propriétés des exposants et, accessoirement, sur la résolution d’équations quadratiques.
On sait que n’importe quelle base non nulle affectée de l’exposant \(0\) est \(1\). On peut donc commencer par chercher pour quelles valeurs de \(x\) a-t-on \[x^{2}-9x + 20 = 0\]En utilisant la méthode somme-produit, on peut factoriser le trinôme \begin{align*}x^{2}-9x + 20 &= 0 \\ \\ x^{2}-5x-4x+20&=0 \\ \\ x\left(x-5\right)-4\left(x-5\right)&=0 \\ \\ (x-5)(x-4)&=0\end{align*}Les deux solutions sont donc \(x=4\) et \(x=5\). Attention ! On doit d’abord vérifier que la base ne soit pas nulle car \(0^0\) serait une forme indéterminée. Puisque \begin{align*}(4)^{2}-5(4)+5 &= 16-20+5 \\ \\ &=1 \\ \\ &\neq 0\end{align*}et\begin{align*}(5)^{2}-5(5) + 5 &= 25-25 + 5 \\ \\ &=5 \\ \\ &\neq 0\end{align*}on accepte ces deux solutions.
On sait aussi que n’importe quelle puissance de \(1\) est \(1\). On peut donc trouver pour quelles valeurs de \(x\) a-t-on \[x^{2}-5x+5=1\]Par hasard, à l’étape précédente, on a trouvé que \(x = 4\) est une solution. Sinon, on procède comme d’habitude \begin{align*}x^{2}-5x+5&=1 \\ \\ x^{2}-5x+4&=0 \\ \\ x^{2}-x-4x+4&=0 \\ \\ x(x-1)-4(x-1)&=0 \\ \\ (x-1)(x-4)&=0 \end{align*}Les deux solutions sont \(x=1\) et \(x = 4\) (la deuxième était attendue).
Voilà ! On a trois solutions, \(1\), \(4\), et \(5\). Lorsqu’on utilise Desmos ou Géogébra, cela semble confirmer nos résultats 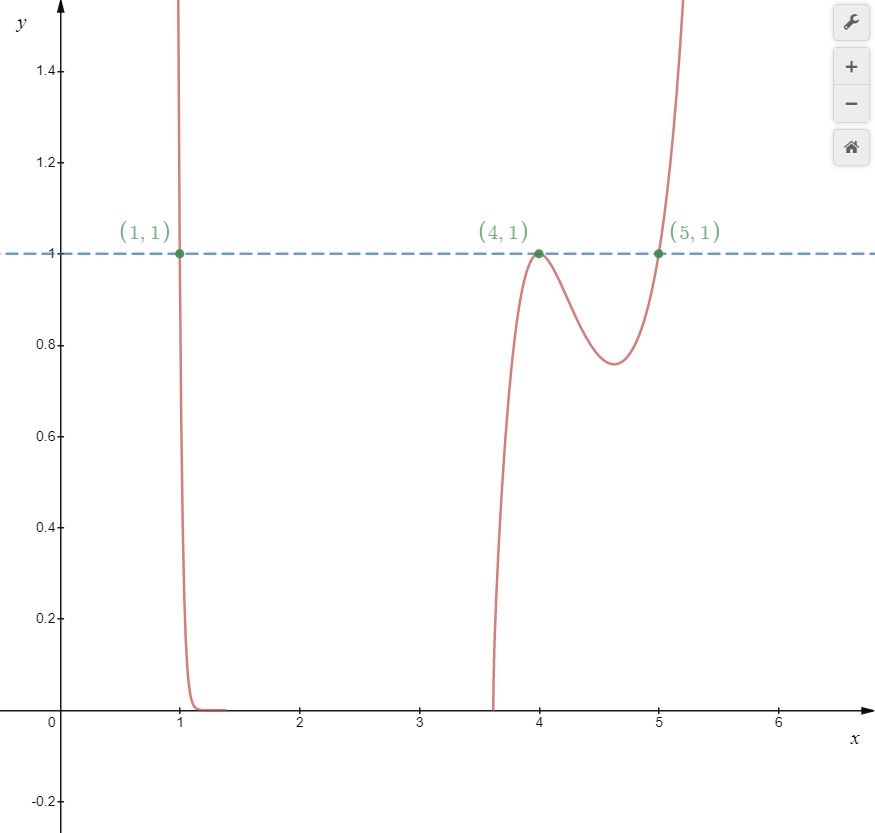
dans Desmos
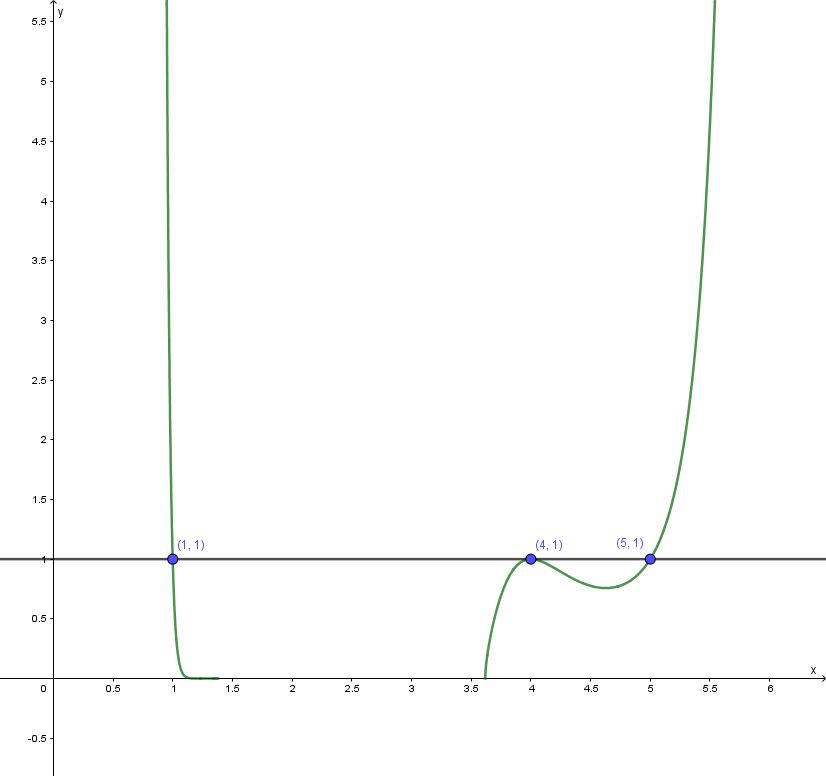
dans Géogébra
C’est aussi ce que l’élève a obtenu. Cependant, c’est incomplet 😲 !
Bien que Desmos et Géogébra semble suggérer le contraire, un cas à traiter a été oublié. Il est possible que la puissance soit \(1\) si la base est \(-1\) et l’exposant est pair. En résolvant \[x^{2}-5x+5=-1\]on obtient \begin{align*}x^{2}-5x+5 &=-1 \\ \\ x^{2}-5x+6 &=0 \\ \\ x^{2}-3x-2x+6&=0 \\ \\ x(x-3)-2(x-3)&=0 \\ \\(x-3)(x-2)&=0\end{align*}Il semble y avoir deux solutions additionnelles \(x=2\) et \(x = 3\). Vérifions si pour ces valeurs l’exposant est pair. Pour \(x=2\), c’est clair puisque les trois termes \[2^{2}-9(2)+20\] sont pairs et pour \(x=3\), \begin{align*}(3)^{2}-9(3)+20 &=9-27+20 \\ \\ &=2\end{align*}on obtient un nombre pair aussi !
Il y a donc deux solutions additionnelles, soit cinq au total, c’est-à-dire \(1\), \(2\), \(3\), \(4\) et \(5\). Pourquoi Desmos et Géogébra ne semblaient nous donner que 3 solutions ? C’est que sur l’intervalle \begin{align*}x^{2}-5x+5\leq 0 \\ \\ x^{2}-5x\leq-5 \\ \\ x^{2}-5x+\frac{25}{4}\leq-5+ \frac{25}{4}\\ \\ \left(x- \frac{5}{2}\right)^2 \leq -\frac{20}{4} + \frac{25}{4} \\ \\ \left(x-\frac{5}{2}\right)^{2} \leq \frac{5}{4} \\ \\-\sqrt{\frac{5}{4}}\leq x -\frac{5}{2}\leq \sqrt{\frac{5}{4}} \\ \\ -\frac{\sqrt{5}}{2}\leq x-\frac{5}{2} \leq \frac{\sqrt{5}}{2}\\ \\ \frac{5-\sqrt{5}}{2} \leq x \leq \frac{5+\sqrt{5}}{2}\end{align*}la base est négative. Le logiciel n’affiche pas l’exponentielle sur cet intervalle. On note que \(\frac{5-\sqrt{5}}{2}\approx 1,\!38\) et \(\frac{5+\sqrt{5}}{2}\approx 3,\!62\) et que cela concorde avec les graphiques ci-dessus.
Avec la bonne syntaxe, WolframAlpha n’est pas berné !
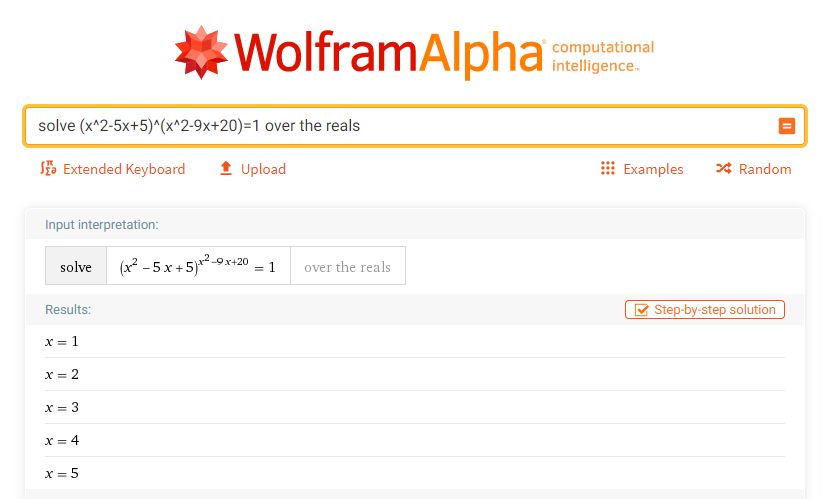
Excellente comparaison des logiciels (je ne connaissais pas Desmos). Et on retrouve le non moins excellent Mathematica (moteur du WolframAlpha). Et je n’ai pas le temps de tout éplucher mais je parie que le site dans son entier est excellent. Qui plus est mis à jour récemment :) J’étais venu pour les conchoïde et n’est pas été déçu. Je paierai mon pot électronique et je m’inscrirai au flux RSS si je pouvais. Merci
Bonjour Stéphane,
merci du commentaire :-)
Je manque un peu de temps pour écrire régulièrement, mais le site me tient à cœur.
RSS : https://www.thedudeminds.net/?feed=rss2
Au plaisir !