
Après avoir lu le livre de Robert Bosch, Opt Art : From Mathematical Optimization to Visual Design (ici), je me suis affairé avec quelques élèves du Club de Math de mon école à réaliser ce portrait de Louis Riel. Nous avons utilisé \(15\) jeux complets de \(55\) dominos double neuf et les méthodes décrites dans le livre pour réaliser l’œuvre (pour les intéressés, on trouve un solver en ligne ici).
Après avoir travaillé autant avec des dominos en compagnie des élèves, quelques questions sont apparues naturellement.
Le nombre de dominos dans un jeu
Un jeu de dominos double six
D’abord, je dois avouer qu’avant la lecture du livre, je ne savais même pas qu’existaient des dominos autres que les classiques dominos double six. C’est la première fois que je manipulais des dominos double neuf. J’ai également appris que des dominos double douze étaient populaires (par exemple pour jouer à la variante la plus répandue du jeu du Train mexicain).
Un jeu de dominos double neuf
Combien de pièces comporte un jeu de dominos ? Chaque couple de deux nombres, avec répétition, est représenté une unique fois. En combinatoire, il s’agit des combinaisons avec répétitions. Il y a \[ \left(\! \! \binom{n}{k}\! \!\right) = \frac{(n+k-1)!}{k! \, (n-1)!}\]façons de choisir \(k\) éléments dans un ensemble de \(n\) éléments, sans ordre, mais avec répétitions. Il y a \(p+1\) nombres différents sur des dominos à \(p\) points (il faut compter le zéro) et on choisit \(2\) de ces nombres. On pose \(n = p+1\) et \(k = 2\) pour obtenir \begin{align*} \left(\! \!\binom{p+1}{2}\! \!\right) = \frac{(p+1+2-1)!}{2! \, (p+1-1)!} &= \frac{(p+2)!}{2! \,p!} \\ \\ &= \frac{(p+2)(p+1)\, p!}{2\, p!} \\ \\ &= \frac{(p+2)(p+1)}{2}\end{align*}
Lorsqu’on dispose les dominos sur la table tel qu’illustré dans les deux images précédentes, cette valeur, \(\frac{(p+2)(p+1)}{2}\) n’a rien de surprenante : cela correspond à la somme des \(p+1\) premiers entiers : \[\frac{(p+1)((p+1)+1)}{2} = \frac{(p+1)(p+2)}{2}\]En outre, il y a \(\frac{(6+2)(6+1)}{2} = \frac{56}{2} = 28\) dominos dans un jeu double six, \(\frac{(9+2)(9+1)}{2} = \frac{110}{2} = 55\) dominos dans un jeu double neuf et \(\frac{(12+2)(12+1)}{2} = \frac{182}{2} = 91\) dominos dans un jeu double douze.
Le grand tour
Même avec assez peu d’effort, il est possible de disposer tous les dominos d’un jeu double six pour compléter une boucle, comme dans l’image ci-dessous.
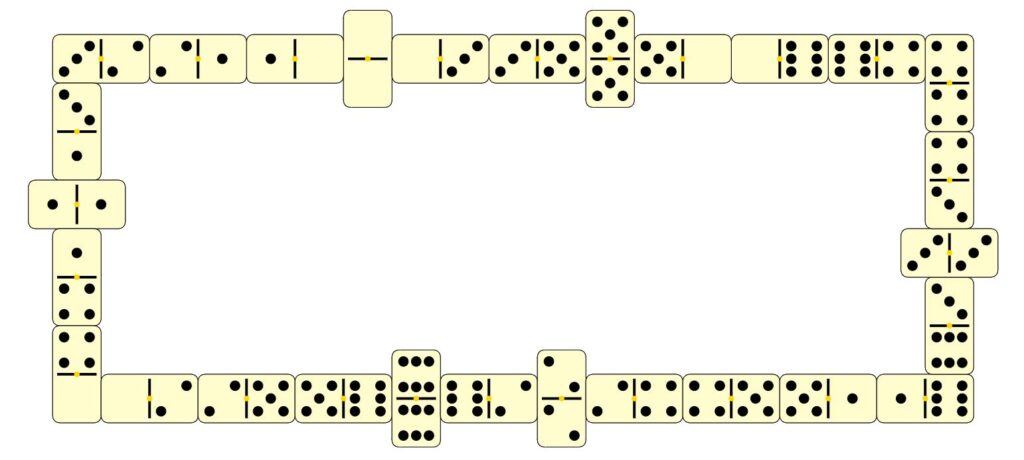
Dans cet exemple, j’ai utilisé des dominos double six. Or, lorsqu’on a essayé de compléter une boucle avec des dominos double neuf, on a essuyé plusieurs échecs. Est-il impossible de compléter des boucles en utilisant certains jeux comme le double neuf ?
On peut répondre à cette question en utilisant les graphes. Chaque sommet du graphe ci-dessous représente un nombre et chaque arête représente un domino : une arête relie deux sommets, ce sont les deux nombres qui apparaissent sur le domino correspondant. Notons aussi que le graphe comporte des arêtes qui ont le même sommet de départ et d’arrivée : ce sont les dominos doubles ( \(\{1, 1\}\), \(\{2, 2\}\), \(\{3, 3\}\), etc. )
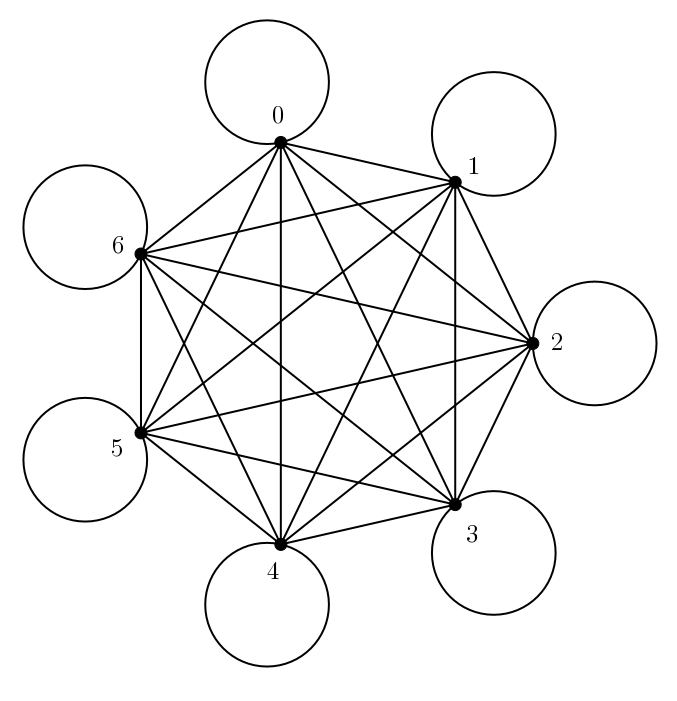
Incidemment, l’image suggère une troisième façon de compter le nombre de dominos dans un jeu. Il y a \(p+1\) sommets, puisqu’on ajoute le sommet pour le nombre zéro. Chaque sommet est relié aux \(p\) autres sommets puis à lui-même : il y a donc \(p+2\) arêtes issues de chaque sommet (c’est le degré de chaque sommet). Le nombre d’arêtes est \[\frac{(p+1)(p+2)}{2}\]en n’oubliant pas de diviser par \(2\) pour ne pas compter chaque arête deux fois (elles ont deux extrémités).
Cela nous permet de découvrir facilement s’il est possible de former une boucle avec les dominos : il s’agit de trouver un cycle eulérien dans le graphe. Un graphe comporte un cycle eulérien si et seulement si tous ses sommets possèdent un degré pair. Puisque le degré de chaque sommet est \(p+2\), cela sera le cas précisément lorsque \(p\) est pair. Lorsque \(p\) est impair, il n’y a pas de cycle eulérien, donc aucune boucle possible. Ainsi, avec un jeu double six ou un jeu double douze, il est possible (et relativement facile) de compléter une boucle : les degrés de tous les sommets de leur graphe sont respectivement \(8\) et \(14\). Mais dans un jeu double neuf les tentatives seront vaines : aucune boucle n’est possible car chaque sommet à un degré \(11\).
La boucle avec un jeu double six présentée précédemment et le cycle eulérien du graphe correspondant
Est-il au moins possible de jouer tous les dominos dans un jeu double neuf (ou un jeu avec un nombre de points impair) sans former une boucle ?

Est-il possible de jouer tous les dominos d’un jeu double neuf sans devoir compléter une boucle ?
Hélas, non ! Il est possible de former une chaîne eulérienne si et seulement si le graphe comporte exactement deux sommets de degré impair. Or, un jeu double neuf comporte \(10\) sommets de degré impair. Il n’est donc pas possible de former une chaîne eulérienne.
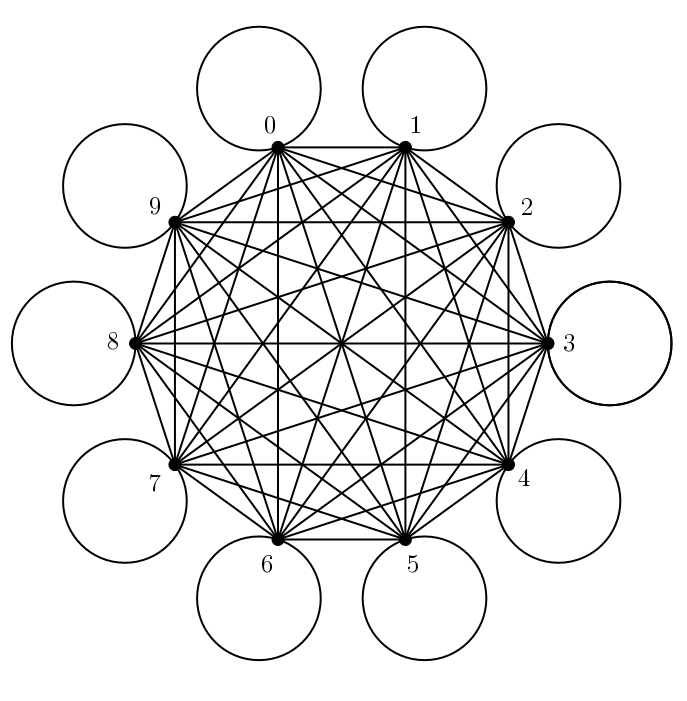
Le graphe d’un jeu double neuf
En d’autres mots, même en laissant tomber l’idée de boucle, il n’est même pas possible de jouer tous les dominos pour former une longue chaîne. En fait, le seul jeu de dominos avec un nombre de points impairs dans lequel une telle chaîne serait possible serait représenté par un graphe à deux sommets : \(0\) et \(1\).

Il s’agit du jeu double un.
Pas très excitant !
