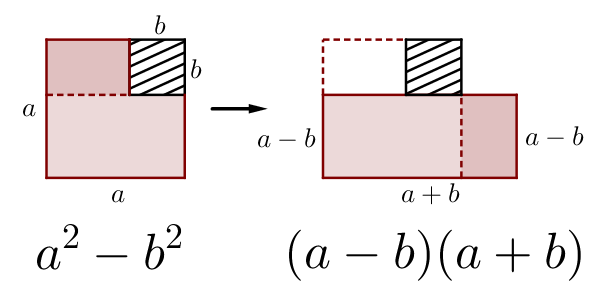
Très tôt à l’école on apprend à factoriser la différence de carrés \[a^{2}-b^{2}=(a-b)(a+b)\]
Puis, les manuels renferment habituellement des exercices « avancés » qui font intervenir des différences de deux puissances dont les exposants sont eux-mêmes des puissances de \(2\). Les auteurs s’attendent à ce que l’élève applique plusieurs fois la différence de carrés. À titre d’exemple, on considère\begin{align*} a^{8}-b^{8}&=\left(a^{4}\right)^{2}-\left(b^{4}\right)^{2} \\ \\ &=\left(a^{4}-b^{4}\right)\left(a^{4}+b^{4}\right) \\ \\ &=\left(\left(a^{2}\right)^{2}-\left(b^{2}\right)^{2}\right)\left(a^{4}+b^{4}\right) \\ \\ &=\left(a^{2}-b^{2}\right)\left(a^{2}+b^{2}\right)\left(a^{4}+b^{4}\right) \\ \\ &=(a-b)(a+b)\left(a^{2}+b^{2}\right)\left(a^{4}+b^{4}\right)\end{align*}Qu’en est-il des autres binômes ? Qu’en est-il des différences de deux puissances en général ? De sommes de deux puissances ?
Différences de deux puissances
Pour les différences de puissances plus élevées, les nouvelles sont excellentes ! On peut toujours factoriser ! Certains, d’ailleurs, connaissent déjà par cœur la factorisation de la différence de cubes, \[a^{3}-b^{3} = (a-b)\left(a^{2} + ab + b^{2}\right)\] La factorisation est obtenue grâce à cette identité \[a^{n}-b^{n} = (a-b)\left(a^{n-1}+a^{n-2}b + a^{n-3}b^{2} + \ \dots \ + \ a^{2}b^{n-3} + ab^{n-2} + b^{n-1}\right)\]ou, si on préfère, \[a^{n}-b^{n} = (a-b)\sum_{j=0}^{n-1}a^{n-j-1}b^j\] pour \(n \in \mathbb{N}^{*}\), et dont on peut tirer \[a^{3}-b^{3} = (a-b)\left(a^{2} + ab + b^{2}\right)\]pour les cubes, \[a^{4}-b^{4} = (a-b)\left(a^{3}+a^{2}b + ab^{2} + b^{3}\right)\]pour les quatrièmes puissances (notons qu’ici le deuxième facteur, \(a^{3}+a^{2}b+ab^{2}+b^{3}\), se factorise davantage en effectuant une mise en évidence double si on cherche la factorisation complète sans recourir plusieurs fois à la différence de carrés tel qu’expliqué précédemment[1]), \[a^{5}-b^{5} = (a-b)\left(a^{4} + a^{3}b + a^{2}b^{2}+ ab^{3} + b^{4}\right)\]pour les cinquièmes puissances, etc. En observant bien les termes dans les parenthèses ou en effectuant les multiplications, on se rend bien vite compte de la raison pour laquelle cela fonctionne. Et cela peut nous inspirer une démonstration.
Directe
La preuve directe dépend essentiellement des deux égalités suivantes, presque identiques. On peut prendre quelques minutes pour se convaincre que\[\sum_{j=1}^{n-1}a^{n-j}b^{j} = \sum_{j=1}^{n-1}a^{j}b^{n-j}\]et\[\sum_{j=0}^{n-1}a^{n-j-1}b^{j} = \sum_{j=0}^{n-1}a^{j}b^{n-j-1}\]Ainsi, en utilisant les égalités précédentes respectivement à la deuxième ligne et à l’avant dernière ligne, on peut simplement écrire \begin{align*}a^{n}-b^{n}&=a^{n} + \sum_{j=1}^{n-1}a^{n-j}b^{j}-\sum_{j=1}^{n-1}a^{n-j}b^{j}-b^{n}\\ \\ &=a^{n} + \sum_{j=1}^{n-1}a^{n-j}b^{j}-\sum_{j=1}^{n-1}a^{j}b^{n-j}-b^{n} \\ \\ &=\sum_{j=0}^{n-1}a^{n-j}b^{j}-\sum_{j=0}^{n-1}a^{j}b^{n-j} \\ \\&=a\sum_{j=0}^{n-1}a^{n-j-1}b^{j}-b\sum_{j=0}^{n-1}a^{j}b^{n-j-1} \\ \\ &= a\sum_{j=0}^{n-1}a^{n-j-1}b^{j}-b\sum_{j=0}^{n-1}a^{n-j-1}b^{j} \\ \\ &=\left(a-b\right)\sum_{j=0}^{n-1}a^{n-j-1}b^{j}\end{align*}
Par induction
D’abord on remarque que \begin{align*}a^{1}-b^{1} &=(a^{1}-b^{1})\sum_{j=0}^{0}a^{1-j-1}b^{j} \\ \\ &=(a-b)a^{1-0-1}b^{0} \\ \\ &=(a- b)(1)\end{align*}C’est la base de l’induction. On pose ensuite l’hypothèse. Pour tout \(q\) tel que \(1 \leq q \leq k\), on a \[a^{q}-b^{q} = (a-b)\sum_{j=0}^{q-1}a^{q-j-1}b^j\]On travaille donc avec le binôme \(a^{k+1}-b^{k+1}\) et on cherche l’hérédité. La prochaine étape est loin d’être intuitive : on fait apparaître des termes de la forme \(a^{k}b\) et \(ab^{k}\). On obtient \[a^{k+1}-ab^{k} + a^{k}b-b^{k+1}-a^{k}b+ ab^{k}\]et une mise en évidence double nous donne \[a\left(a^{k}-b^{k}\right) + b\left(a^{k}-b^{k}\right)-a^{k}b+ ab^{k}\] \[(a+b)\left(a^{k}-b^{k}\right)-a^{k}b+ ab^{k}\]puis une mise en évidence simple sur les derniers termes \[(a+b)\left(a^{k}-b^{k}\right)-ab\left(a^{k-1}-b^{k-1}\right)\]Notre hypothèse d’induction (qu’on utilise deux fois) nous permet ensuite d’écrire \[(a+b)(a-b)\sum_{j=0}^{k-1}a^{k-j-1}b^{j}-ab(a-b)\sum_{j=0}^{k-2}a^{k-j-2}b^{j}\]Puis on met en évidence \(\left(a-b\right)\)\[\left(a-b\right)\left((a+b)\sum_{j=0}^{k-1}a^{k-j-1}b^{j}-ab\sum_{j=0}^{k-2}a^{k-j-2}b^j\right)\]La majeure partie du travail étant faite, il reste à distribuer et regrouper. D’abord, \[\left(a-b\right)\left(\sum_{j=0}^{k-1}a^{k-j}b^{j} + \sum_{j=0}^{k-1}a^{k-j-1}b^{j+1}-\sum_{j=0}^{k-2}a^{k-j-1}b^{j+1}\right)\]puis sortir le \(k-1\)e terme de la sommation du centre \[\left(a-b\right)\left(\sum_{j=0}^{k-1}a^{k-j}b^{j} + \sum_{j=0}^{k-2}a^{k-j-1}b^{j+1} + a^{k-(k-1)-1}b^{k-1+1}-\sum_{j=0}^{k-2}a^{k-j-1}b^{j+1}\right)\]soit\[\left(a-b\right)\left(\sum_{j=0}^{k-1}a^{k-j}b^{j} + \sum_{j=0}^{k-2}a^{k-j-1}b^{j+1} + a^{0}b^{k}-\sum_{j=0}^{k-2}a^{k-j-1}b^{j+1}\right)\]On simplifie les sommes \[\left(a-b\right)\left(\sum_{j=0}^{k-1}a^{k-j}b^{j} + a^{0}b^{k}\right)\]et on insère brillamment le terme \(a^{0}b^{k}\) dans la somme. \[\left(a-b\right)\left(\sum_{j=0}^{k}a^{k-j}b^{j}\right)\]L’hérédité tient ! On a bien \[a^{k+1}-b^{k+1}=\left(a-b\right)\sum_{j=0}^{(k+1)-1}a^{(k+1)-j-1}b^{j}\]Voilà !
Sommes de deux puissances
Pour ce qui est des sommes de deux puissances, c’est plus délicat. D’abord, au moment où on apprend à reconnaître les différences de carrés, on se fait aussi dire que la somme, \(a^{2} + b^{2}\), ne se factorise pas. Soit. Qu’en est-il des sommes de puissances plus élevées ? Pour les puissances impaires, on peut trouver une factorisation. C’est donc dire que \(a^{3} + b^{3}\) se factorise, c’est \[a^{3} + b^{3} = (a + b)(a^{2}-ab+b^{2})\]En général, on a, pour \(n\) impair, \[a^{n} + b^{n} = (a + b)\left(a^{n-1}-a^{n-2}b + a^{n-3}b^{2}\ – \ \dots \ – \ ab^{n-2} + b^{n-1}\right)\]alternant les signes des termes dans la grande parenthèse. En posant \(n = 2k + 1\), on obtient \[a^{2k+1} + b^{2k+1} = (a + b)\left(a^{2k}-a^{2k-1}b + a^{2k-2}b^{2}\ – \ \dots\ – \ ab^{2k-1} + b^{2k}\right)\]pour \(k\in \mathbb{N}\). Par exemple, pour \(a^{5}+b^{5}\) on obtient \[a^{5}+b^{5} = (a + b) \left(a^{4}-a^{3}b+a^{2}b^{2}-ab^{3}+b^{4}\right)\]
Pour la démonstration, on utilise la différence de deux puissances démontrée précédemment. On se rappelle que \[a^{n}-b^{n} = (a-b)\sum_{j=0}^{n-1}a^{n-j-1}b^{j}\]On note aussi que puisque \(2k+1\) est impair, \(-\left(b^{2k+1}\right) = \left(-b\right)^{2k+1}\). On obtient \begin{align*}a^{2k+1} + b^{2k+1} &= a^{2k+1}-\left(-\left(b^{2k+1}\right)\right) \\ \\ &=a^{2k+1} – \left(-b\right)^{2k+1} \\ \\ &=\left(a – (-b)\right) \sum_{j=0}^{2k}a^{2n-j}\left(-b\right)^{j} \\ \\ &=(a + b)\sum_{j=0}^{2k}\left(-1\right)^{j}a^{2k-j}b^{j} \\ \\ &=(a+b)\left(a^{2k}-a^{2k-1}b+a^{2k-2}b^{2}\ -\ \dots \ – \ ab^{2k-1} + b^{2k}\right) \end{align*}Simple et brillant ! Le facteur \(\left(-1\right)^{j}\) alterne entre \(1\) et \(-1\) selon la parité de \(j\).
Est-ce tout ? Non. On peut utiliser ce résultat pour factoriser des sommes de puissances paires. En effet, disons qu’on ait à factoriser \(a^{n} + b^{n}\) pour \(n\) quelconque. On exprime \(n\) comme le produit de deux facteurs : la plus grande puissance de \(2\) possible et un facteur impair. En d’autres mots, on pose \[n = 2^{p}q\]tel que \(p\) est le plus grand nombre possible et donc que \(q\) est impair. En se rappelant que \(x^{rs} = \left(x^{r}\right)^{s}\), on obtient \begin{align*}a^{n} + b^{n} &= a^{2^{p}q} + b^{2^{p}q} \\ \\ &=\left(a^{2^{p}}\right)^{q} + \left(b^{2^{q}}\right)^{q} \\ \\ &=\left(a^{2^{p}} + b^{2^{p}}\right)\left(\left(a^{2^{p}}\right)^{q-1}-\left(a^{2^{p}}\right)^{q-2}\left(b^{2^{p}}\right) \ – \ \dots \ – \ \left(a^{2^{p}}\right) \left(b^{2^{p}}\right)^{q-2} + \left(b^{2^{p}}\right)^{q-1}\right)\\ \\ &=\left(a^{2^{p}} + b^{2^{p}}\right)\left(a^{2^{p}(q-1)}-a^{2^{p}(q-2)}b^{2^{p}} \ – \ \dots \ – \ a^{2^{p}} b^{2^{p}(q-2)} + b^{2^{p}(q-1)}\right)\end{align*}Un exemple s’impose. Si on voulait factoriser \(a^{6} + b^{6}\) on procéderait comme suit : sachant que \(6 = 2 \cdot 3\), on obtient \begin{align*}a^{6}+b^{6}&= \left(a^{2}\right)^{3} + \left(b^{2}\right)^{3} \\ \\&= \left(a^{2}+b^{2}\right) \left(\left(a^{2}\right)^{2} – \left(a^{2}\right)\left(b^{2}\right) + \left(b^{2}\right)^{2}\right) \\ \\ &= \left(a^{2}+b^{2}\right) \left(a^{4}-a^{2}b^{2}+b^{4}\right)\end{align*}Les nombres qui ne peuvent être exprimés d’une telle manière, c’est-à-dire \(n = 2^{p}q\) tel que \(q \neq 1\), sont les puissances de \(2\). Ainsi, ce sont les binômes \[a^{2} + b^{2}\] \[a^{4} + b^{4}\] \[a^{8} + b^{8}\] \[a^{16} + b^{16}\] \[\dots\]qui ne sont pas factorisables…
Plus loin encore
… ou le sont-ils ? Hmmmm… S’ils ne sont effectivement pas factorisables en des polynômes avec coefficients entiers ou rationnels, en d’autres mots, s’ils ne sont pas factorisables dans \(\mathbb{Z}\) ou \(\mathbb{Q}\), en revanche ils le sont dans \(\mathbb{R}\), sauf pour \(a^{2}+ b^{2}\). En effet, par exemple, pour \(a^{4}+b^{4}\), on réarrange l’expression pour faire apparaître un trinôme carré parfait, qu’on factorise, puis on factorise la différence de carrés obtenue :\begin{align*}a^{4} + b^{4} &= a^4 + 2a^{2}b^{2}+b^{4}-2a^{2}b^{2} \\ \\ &=\left(a^{2}+ b^{2}\right)^{2}-2a^{2}b^{2} \\ \\ &= \left(a^{2}+ b^{2}\right)^{2}-\left(\sqrt{2}ab\right)^{2} \\ \\ &= \left(a^{2} + b^{2}-\sqrt{2}ab\right)\left(a^{2} + b^{2}+ \sqrt{2}ab\right) \\ \\ &= \left(a^{2}-\sqrt{2}ab+b^{2}\right)\left(a^{2}+\sqrt{2}ab+b^{2}\right)\end{align*}Le lecteur aguerri peut effectuer la multiplication à des fins de vérification. On souligne ici que la factorisation est différente des précédentes présentées jusqu’ici dans ce billet du fait que des coefficients ne sont pas entiers (ou même rationnels). Plus généralement, si \(n = 2^{k}\), on a \begin{align*}a^{n} + b^{n} &= a^{2^{k}} + b^{2^{k}} \\ \\ &= a^{2^{k}} + 2a^{2^{k-1}}b^{2^{k-1}} + b^{2^{k}}-2a^{2^{k-1}}b^{2^{k-1}}\\ \\ &=\left(a^{2^{k-1}}+b^{2^{k-1}}\right)^{2}-2a^{2^{k-1}}b^{2^{k-1}} \\ \\ &=\left(a^{2^{k-1}}+b^{2^{k-1}}\right)^{2}-\left(\sqrt{2}a^{2^{k-2}}b^{2^{k-2}}\right)^{2}\\ \\ &=\left(a^{2^{k-1}}+b^{2^{k-1}}-\sqrt{2}a^{2^{k-2}}b^{2^{k-2}}\right)\left(a^{2^{k-1}}+b^{2^{k-1}} + \sqrt{2}a^{2^{k-2}}b^{2^{k-2}} \right) \\ \\ &=\left(a^{2^{k-1}}-\sqrt{2}a^{2^{k-2}}b^{2^{k-2}}+b^{2^{k-1}} \right)\left(a^{2^{k-1}}+\sqrt{2}a^{2^{k-2}}b^{2^{k-2}}+b^{2^{k-1}} \right)\end{align*}On voit que ça ne fonctionne pas pour \(a^{2}+b^{2}\) car dans ce cas \begin{align*}a^{2}+b^{2}&=a^{2} + 2ab + b^{2}-2ab \\ \\ &=\left(a+b\right)^{2}-2ab \\ \\ &= \left(a + b\right)^{2}-\left(\sqrt{2}a^{\frac{1}{2}}b^{\frac{1}{2}}\right)^{2} \\ \\ &=\left(a-\sqrt{2}a^{\frac{1}{2}}b^{\frac{1}{2}}+b\right)\left(a +\sqrt{2}a^{\frac{1}{2}}b^{\frac{1}{2}}+b\right)\end{align*}On n’a plus un polynôme valide car les exposants affectés à \(a\) et \(b\) ne sont plus entiers. Ainsi, \(a^{2} + b^{2}\) n’est finalement pas factorisable…
Plus loin encore (bis)
… dans \(\mathbb{R}\). À l’instar de ce qu’on vient de faire, soit passer de \(\mathbb{Z}\) ou \(\mathbb{Q}\) à \(\mathbb{R}\) pour factoriser une expression du genre \(a^{2^{k}}+b^{2^{k}}\), où \(k>1\), on peut passer à \(\mathbb{C}\) pour factoriser \(a^{2} + b^{2}\). En effet, \begin{align*}a^{2} + b^{2} &= a^{2}-\left(-b^{2}\right)\\ \\ &=a^{2}-\left(i^{2}b^{2}\right) \\ \\ &= a^{2}-\left(ib\right)^{2} \\ \\ &=(a-ib)(a + ib)\end{align*}Dans cette dernière factorisation, des coefficients sont des nombres complexes. Voilà !
[1]C’est-à-dire qu’on obtient \begin{align*}a^{4}-b^{4}&=(a-b)\left(a^{3}+a^{2}b+b^{2}a+b^{3}\right) \\ \\ &=(a-b)\left(a^{2}\left(a+b\right) + b^{2}\left(a+b\right)\right) \\ \\ &=(a-b)(a+b)\left(a^{2}+b^{2}\right)\end{align*}ce qui est équivalent à \begin{align*}a^{4}-b^{4}&=\left(a^{2}\right)^{2}-\left(b^{2}\right)^{2} \\ \\ &=\left(a^{2}-b^{2}\right)\left(a^{2}+b^{2}\right) \\ \\ &=(a-b)(a+b)\left(a^{2}+b^{2}\right)\end{align*}