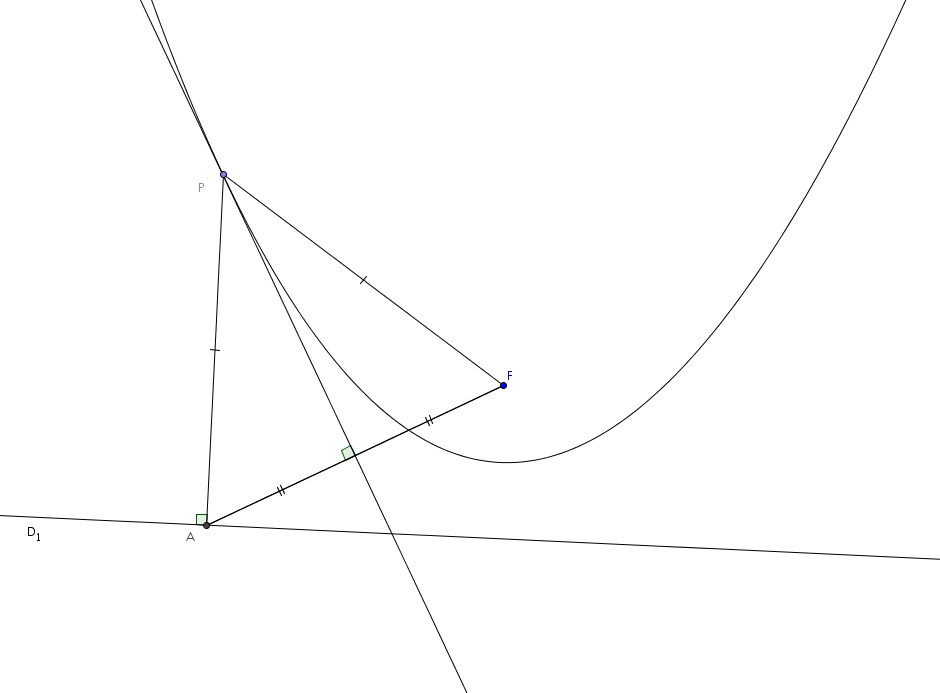
Considérons la parabole suivante, avec son foyer \(F\) et sa droite directrice \(D_{1}\) et un point \(P\) sur cette parabole.
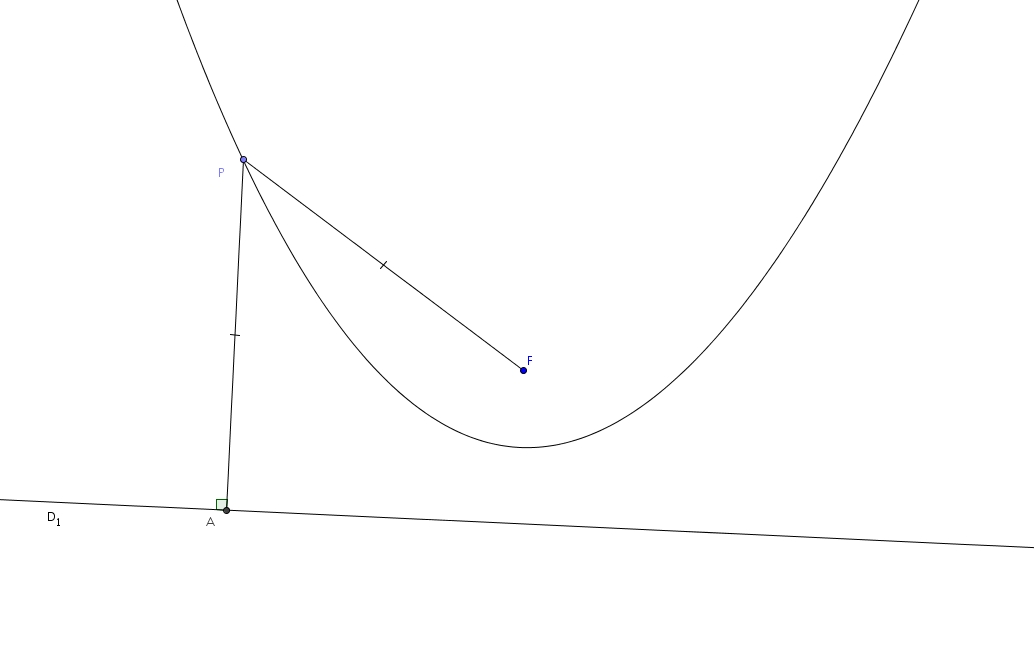 Comme tout point de la parabole est équidistant du foyer et de la droite directrice (sa définition usuelle comme lieu de points), on trouve \[\overline{FP}\cong \overline{AP}\](avec, au passage, \(\overline{AP}\) perpendiculaire à \(D_{1}\)).
Comme tout point de la parabole est équidistant du foyer et de la droite directrice (sa définition usuelle comme lieu de points), on trouve \[\overline{FP}\cong \overline{AP}\](avec, au passage, \(\overline{AP}\) perpendiculaire à \(D_{1}\)).
Relions \(A\) et \(F\). Dans le billet sur la droite d’Euler, on montre que tout point de la médiatrice d’un segment est équidistant des extrémités de ce segment (et réciproquement). Le point \(P\) est donc sur la médiatrice de \(\overline{AF}\).
Bien ! Montrons que cette médiatrice est tangente à la courbe. Dans ce cas, il faudrait que la médiatrice et la parabole ne se touche qu’en un point, le point \(P\). Supposons que la médiatrice coupe la parabole en deux endroits et déduisons une contradiction.
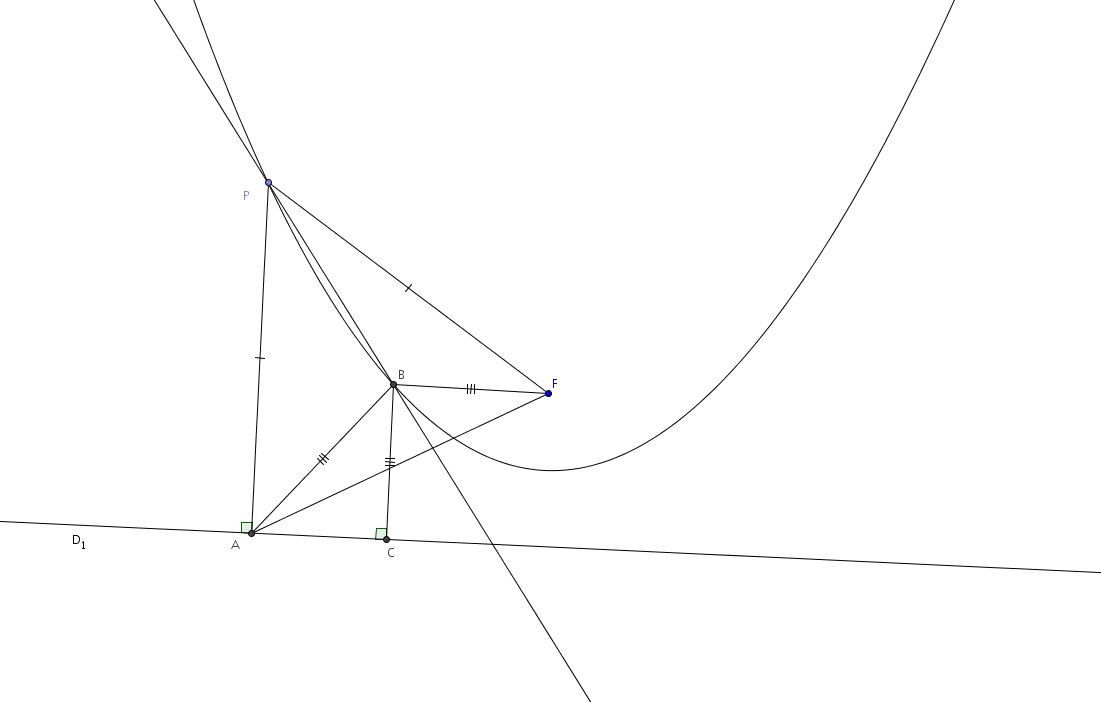
En effet, supposons que la médiatrice de la droite \(AF\) coupe aussi la parabole en \(B\). Comme le point \(B\) est sur la médiatrice, il est à la même distance de \(A\) que de \(F\). On a donc \[\overline{AB}\cong \overline{BF}\]
Or, par définition, si \(B\) est aussi sur la parabole, on trouve aussi \[\overline{BC}\cong \overline{BF}\](encore une fois, ici, \(BC\) perpendiculaire à \(D_{1}\)). Par transitivité, \[\overline{AB}\cong \overline{BC}\]
Est-ce que, vraiment, \(m\overline{AB}\) peut être égal à \(m\overline{BC}\) ? Réfléchissons un peu. Si c’était le cas, alors le triangle \(ABC\) serait isocèle et \(ABC\) étant isocèle, il serait aussi isoangle. Mais comme l’angle \(ACB\) est droit, on aurait aussi \(BAC\) droit. Et alors on obtiendrait ce résultat \begin{align*}m\angle BAC + m\angle ACB + m\angle ABC &= 90^{\circ}+90^{\circ} + m\angle ABC \\ \\ &=180^{\circ}+m\angle ABC \\ \\ &> 180^{\circ}\end{align*}ce qui est la contradiction recherchée. La médiatrice est donc tangente à la parabole. En déplaçant le point \(A\) sur la droite directrice, on obtient donc une infinité de médiatrices toutes tangentes à la parabole. Cela donne lieu à une construction très belle !
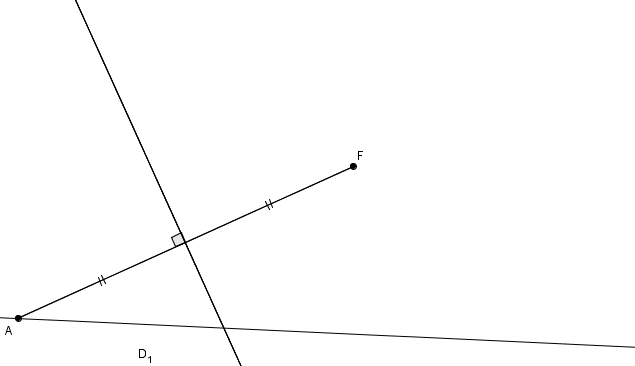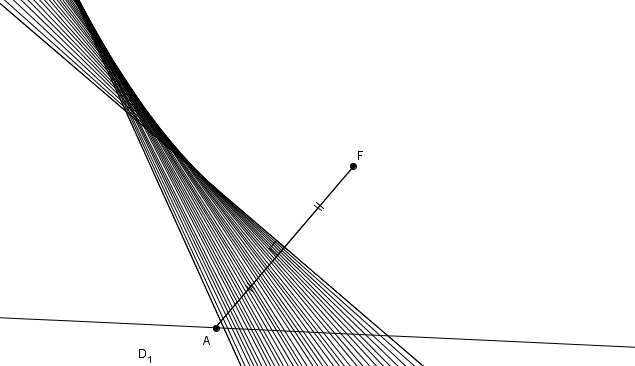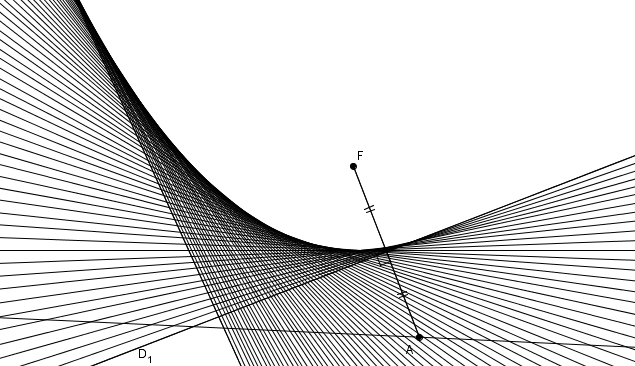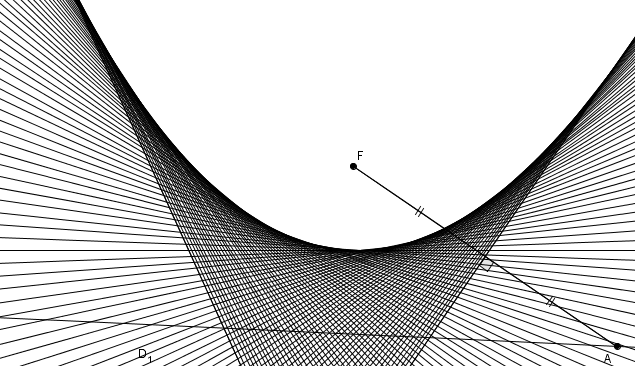
Cette propriété permet aussi d’expliquer la construction de la parabole par pliage.