Vous résolvez des équations avec des racines carrées et vos élèves sont troublés lorsqu’ils élèvent au carré et insèrent peut-être par le fait même une ou des fausses solutions à l’équation initiale ? Par exemple, pour résoudre \[\sqrt{x + 3} = x+1\]on élève au carré pour se débarrasser de la racine carrée à gauche \[x + 3 = \left(x+1\right)^{2}\]On développe \[x + 3 = x^{2}+2x+1\]On regroupe \[0 = x^{2} + x-2\]et on factorise \[0 = (x+2)(x-1)\]Les solutions à la dernière équations sont \(-2\) et \(1\). Si \(1\) est bien une solution de l’équation initiale \begin{align*}\sqrt{1+3} &= 1+1 \\ \\ \sqrt{4}&=2 \\ \\ 2&=2\end{align*}on ne peut pas en dire autant de \(-2\) \begin{align*}\sqrt{-2+3} &\neq -2+1 \\ \\ \sqrt{1}&\neq -1 \\ \\ 1 &\neq -1\end{align*}Lorsqu’on a élevé au carré, une fausse solution, \(-2\), s’est insérée. Calamité !
Exemple extrêêêêêêême
L’intrigue se corse. On veut résoudre\[\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=1\]une expression aux allures certainement plus menaçantes. On cherchera néanmoins à éliminer les racines. En élevant au carré on obtient \[x+3-4\sqrt{x-1}+2\sqrt{\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right)}+x+8-6\sqrt{x-1}=1\]qu’on simplifie en regroupant les termes semblables \[2x+11-10\sqrt{x-1}+2\sqrt{\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right)}=1\]ou de manière équivalente \[2\sqrt{\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right)}=10\sqrt{x-1}-2x-10\]En divisant par \(2\) \[\sqrt{\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right)} = 5\sqrt{x-1}-x-5\]et en élevant au carré pour se débarrasser de la racine à gauche, on obtient \begin{align*}\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right) &= \\ 25x-25-5x\sqrt{x-1}-25\sqrt{x-1}&-5x\sqrt{x-1}+x^{2}+5x-25\sqrt{x-1}+5x+25\end{align*}ou en regroupant les termes semblables \[\left(x+3-4\sqrt{x-1}\right)\left(x+8-6\sqrt{x-1}\right)=x^{2}-10x\sqrt{x-1}+35x-50\sqrt{x-1}\]Dans l’espoir de regrouper les racines de \(x-1\), on développe le produit à gauche \begin{align*}x^{2}+8x-6x\sqrt{x-1}+3x+24-18\sqrt{x-1}-4x\sqrt{x-1}-32\sqrt{x-1}+24x+24 &= \\ x^{2}-10x\sqrt{x-1}+35x-50&\sqrt{x-1}\end{align*}puis on regroupe les termes semblables à gauche, \[x^{2}-10x\sqrt{x-1}+35x-50\sqrt{x-1}=x^{2}-10x\sqrt{x-1}+35x-50\sqrt{x-1}\]et là, ô surprise, une identité ! Vraie pour tout \(x\) ? On a élevé au carré, certes, mais on ne fait quand même pas dans la sorcellerie ! Une identité ! Que s’est-il passé ?
La clé de l’énigme consiste à remarquer que \begin{align*}x+3-4\sqrt{x-1}&=x-1-4\sqrt{x-1}+4 \\ \\ &=\left(\sqrt{x-1}-2\right)^{2}\end{align*}et\begin{align*}x+8-6\sqrt{x-1}&=x-1-6\sqrt{x-1}+9 \\ \\ &=\left(\sqrt{x-1}-3\right)^{2}\end{align*}c’est à dire que l’équation initiale est équivalente à \[\sqrt{\left(\sqrt{x-1}-2\right)^{2}}+\sqrt{\left(\sqrt{x-1}-3\right)^{2}}=1\]ou, exprimée avec des valeurs absolues, à \[\left|\sqrt{x-1}-2\right| + \left|\sqrt{x-1}-3\right| =1\]Maintenant, pour des valeurs de \(x\) telles que\[1\leq x \leq 5\]l’expression \[\sqrt{x-1}-2\]est négative et pour des valeurs de \(x\) telles que \[5\leq x\]l’expression \[\sqrt{x-1}-2\]est positive. D’autre part, pour des valeurs de \(x\) telles que \[1\leq x \leq 10\]l’expression \[\sqrt{x-1}-3\]est négative et pour des valeurs de \(x\) telles que\[10\leq x\]l’expression \[\sqrt{x-1}-3\]est positive. Ainsi, il y a trois cas à traiter. D’abord si \[1\leq x \leq 5\]les deux expressions sont négatives et pour se débarrasser des valeurs absolues on pose \[-\left(\sqrt{x-1}-2\right)-\left(\sqrt{x-1}-3\right) =1\]ce qui fait \[-2\sqrt{x-1}=-4\]puis en divisant par \(-2\) \[\sqrt{x-1}=2\]On trouve ainsi la solution \begin{align*}x-1&=4 \\ \\ x&=5\end{align*}et comme \[5\leq 5\]on accepte cette solution. Le deuxième cas à traiter est \[5\leq x \leq 10\]Dans ce cas, la première expression est positive mais la deuxième est négative. Pour enlever les valeurs absolues, on pose \[\sqrt{x-1}-2-\left(\sqrt{x-1}-3\right)=1\]ce qui fait \[\sqrt{x-1}-2-\sqrt{x-1}+3=1\]ou, ô surprise, \[1=1\]une identité ! C’est donc dire que cet intervalle au complet \[5 \leq x \leq 10\]est aussi solution à l’équation. Enfin, le troisième et dernier cas à considérer est \[10\leq x\]Dans ce cas, les deux expressions sont positives et donc on a \[\sqrt{x-1}-2+\sqrt{x-1}-3=1\]ce qui fait \[2\sqrt{x-1}=6\]puis en divisant par \(2\) \[\sqrt{x-1}=3\]et là on trouve la solution \begin{align*}x-1&=9 \\ \\ x&= 10\end{align*}Et comme\[10\leq10\]on accepte cette solution.
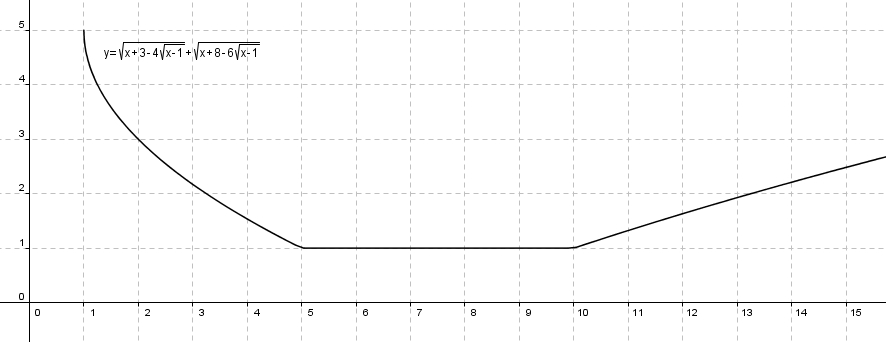
L’ensemble solution à l’équation initiale comprend donc tout l’intervalle fermé \(\left[5,\, 10\right]\) et comporte ainsi une infinité de solutions. Du coup, la stratégie d’élever au carré pour éliminer les racines produit un polynôme qui comporte au moins autant de solutions que l’équation initiale, c’est-à-dire une infinité, et on obtient ainsi une identité.
Références : Edward J. Barbeau (2013), More Fallacies, Flaws and Flimflam
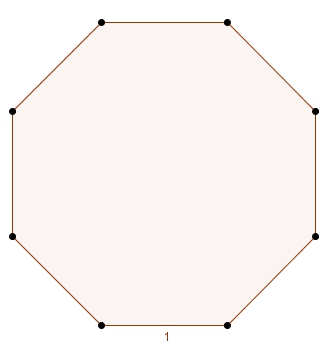
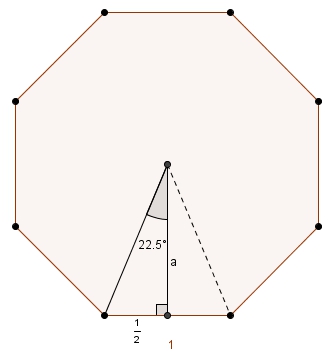
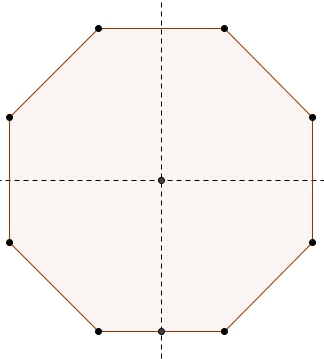
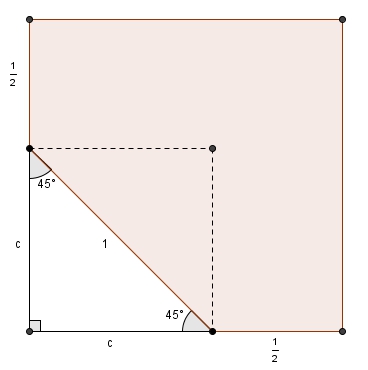
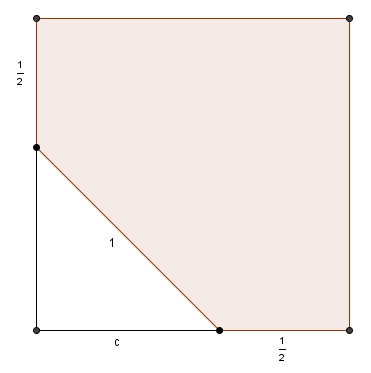 On peut compléter la figure pour obtenir un carré. Il suffirait de soustraire l’aire du triangle rectangle blanc au grand carré. Les angles intérieurs et extérieurs sont au programme du premier cycle. L’angle extérieur d’un octogone régulier étant \(45^{\circ}\), ce triangle blanc est un triangle rectangle isocèle (on aurait pu aussi réfléchir davantage à la symétrie de la figure au lieu de passer par les angles extérieurs).
On peut compléter la figure pour obtenir un carré. Il suffirait de soustraire l’aire du triangle rectangle blanc au grand carré. Les angles intérieurs et extérieurs sont au programme du premier cycle. L’angle extérieur d’un octogone régulier étant \(45^{\circ}\), ce triangle blanc est un triangle rectangle isocèle (on aurait pu aussi réfléchir davantage à la symétrie de la figure au lieu de passer par les angles extérieurs).