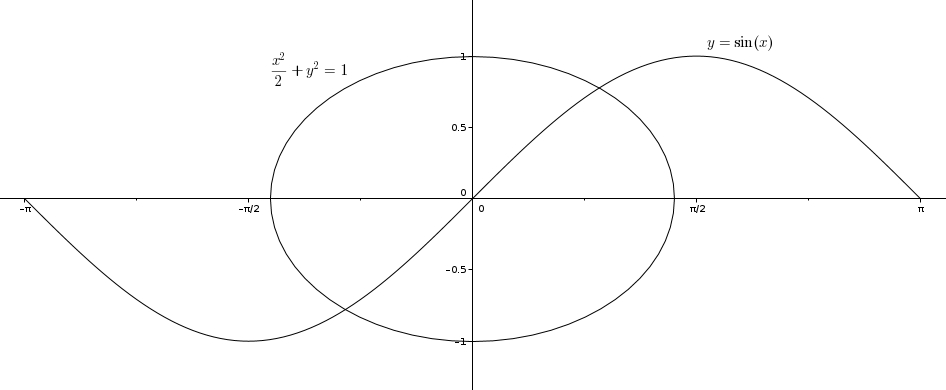
Qu’ont en commun l’ellipse et la fonction sinus dont les équations sont \[\frac{x^{2}}{2} + y^{2} = 1 \quad \text{et} \quad y = \sin(x)\quad ?\]
Et bien ne tombez pas en bas de votre chaise, mais ces deux courbes ont la même longueur ! C’est-à-dire que si l’on considère la fonction sinus sur une période, par exemple entre \(-\pi\) et \(\pi\), tel qu’illustré dans le graphique ci-haut, la longueur de la courbe sera égale au périmètre de l’ellipse.
Avec un peu de calcul différentiel et intégral, on peut trouver une expression représentant la longueur de la courbe sinus entre \(-\pi\) et \(\pi\). Puisque la longueur de la courbe est\[s_{1} = \int_{a}^{b}\sqrt{1 + \left(\frac{\text{d}y}{\text{d}x}\right)^{2}}\text{d}x\]on a dans ce cas-ci \[s_{1} = \int_{-\pi}^{\pi}\sqrt{1 + \cos^{2}\left(x\right)}\, \text{d}x\]D’autre part, en prenant l’équation de l’ellipse, \[\frac{x^{2}}{2} + y^{2}=1\]ou \[\left(\frac{x}{\sqrt{2}}\right)^{2}+y^{2}=1\]et puisque \[\sin^{2}\left(t\right) + \cos^{2}\left(t\right) = 1\]on pose \[\frac{x}{\sqrt{2}}=\sin\left(t\right), \quad y=\cos\left(t\right)\]ce qui nous donne les équations paramétriques de la courbe \[x=\sqrt{2}\sin\left(t\right), \quad y=\cos\left(t\right)\]pour des valeurs de \(t\) \[-\pi\leq t\leq \pi\]Maintenant, avec les équations paramétriques de la courbe, on trouve également une expression pour le périmètre de l’ellipse \[s_{2}= \int_{a}^{b}\sqrt{\left(\frac{\text{d}x}{\text{d}t}\right)^{2}+\left(\frac{\text{d}y}{\text{d}t}\right)^{2}}\text{d}t\]c’est-à-dire que dans ce cas-ci, on a \[s_{2} = \int_{-\pi}^{\pi}\sqrt{\left(\sqrt{2}\cos\left(t\right)\right)^{2} + \left(-\sin\big(t\right)\big)^2}\text{d}t\]ou \[s_{2} = \int_{-\pi}^{\pi}\sqrt{2\cos^{2}\left(t\right) + \sin^{2}\left(t\right)}\,\text{d}t\]En reprenant \(s_{1}\) et en utilisant les substitutions suivantes,\[x = t, \quad \text{d}x = \text{d}t, \quad 1 = \sin^{2}\left(t\right) + \cos^{2}\left(t\right)\]on obtient \begin{align*} s_{1}&=\int_{-\pi}^{\pi}\sqrt{1 + \cos^{2}\left(x\right)}\,\text{d}x \\ \\ &=\int_{-\pi}^{\pi}\sqrt{\sin^{2}\left(t\right) + \cos^{2}\left(t\right) + \cos^{2}\left(t\right)}\, \text{d}t \\ \\ &= \int_{-\pi}^{\pi}\sqrt{2\cos^{2}\left(t\right) + \sin^{2}\left(t\right)} \, \text{d}t \\ \\ &=s_{2}\end{align*}Ah ! La même longueur, effectivement. Mais est-ce que ces manipulations algébriques ne sont que le fruit d’un heureux hasard ? Non ! Quel lien géométrique, fort distrayant s’il existe, unit ellipse et sinusoïde ?
À vos cylindres !
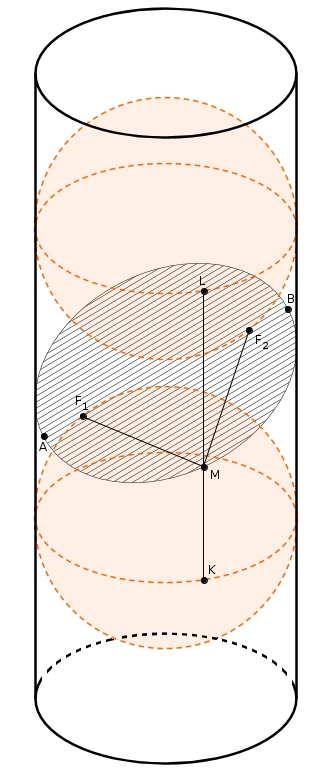
Comme c’est bien connu, l’intersection d’un cylindre circulaire droit et d’un plan (non parallèle au plan qui supporte le cercle directeur, mais ci-après on dira simplement non parallèle aux bases) est une ellipse. On peut considérer le cylindre comme un cône dont l’apex serait « à l’infini ». Autrement, la démarche classique faite avec le cône fonctionne aussi avec le cylindre. Pour étirer le plaisir, voyons. On insère deux sphères de Dandelin (dans le cas du cylindre, les sphères sont isométriques), tangentes au cylindre selon des cercles parallèles aux bases et également tangentes au plan sécant. Les points de tangence au plan sécant correspondent en fait aux foyers de l’ellipse, F1 et F2 comme dans le schéma ci-dessous.
Mes plus fines compétences avec Géogébra et Gimp enfin réunies dans une seule image
On appelle l’intersection du cylindre et du plan \(E\). On trace la droite \(F_{1}F_{2}\) qui intercepte \(E\) en \(A\) et \(B\). On considère un point quelconque \(M\) de \(E\) . On cherche les points \(L\) et \(K\) qui sont en même temps sur les cercles de tangence au cylindre des sphères et sur la droite génératrice qui supporte \(M\). Ainsi, \(L\), \(M\) et \(K\) sont colinéaires. Comme \(MF_{1}\) et \(MK\) sont deux tangentes à une même sphère menées d’un même point extérieur (ici, \(M\)) à la sphère, on a\[m\overline{MF_{1}}=m\overline{MK}\]et de la même manière \[m\overline{MF_{2}}=m\overline{ML}\]En sommant on trouve \[m\overline{MF_{1}}+m\overline{MF_{2}}=m\overline{MK}+m\overline{ML}\]Les cercles de tangence étant parallèles aux bases, \[m\overline{MK}+m\overline{ML} = m\overline{KL} = \text{constante}\]et donc \(E\) est une ellipse \[m\overline{MF_{1}}+m\overline{MF_{2}}=\text{constante}\]dont les points \(F_{1}\) et \(F_{2}\) sont les foyers et dont le segment \(AB\) est le grand axe.
À vos ciseaux !
On sait aussi qu’il est possible de couper, dérouler le cylindre et de le mettre à plat sur la table. On dit que le cylindre est une surface développable. Ce processus (« dérouler » le cylindre) préserve localement les distances. On peut faire le même genre de transformation avec d’autres solides, comme le cône bien entendu, mais pas avec d’autres, comme la sphère. Bref, qu’arrive-t-il lorsqu’on développe un cylindre « tronqué » ?
Mince alors ! Un sinusoïde.
Afin d’y voir plus clair, on considère le (très joli) schéma suivant. Un cylindre circulaire droit de rayon \(r\) a été coupé par un plan suivant un diamètre de sa base et incliné d’un angle \(\theta\), où \(0 < \theta < \frac{\pi}{2}\) (en anglais, ce solide s’appelle un cylindrical wedge). Lorsqu’on met à plat le cylindre, la circonférence se « déroule » selon un axe rectiligne. Ici, on pose \(x\) comme la mesure de l’arc de cercle entre \(A\) et \(B\). La hauteur de la courbe est représentée par la cathète \(y\) du triangle orange.
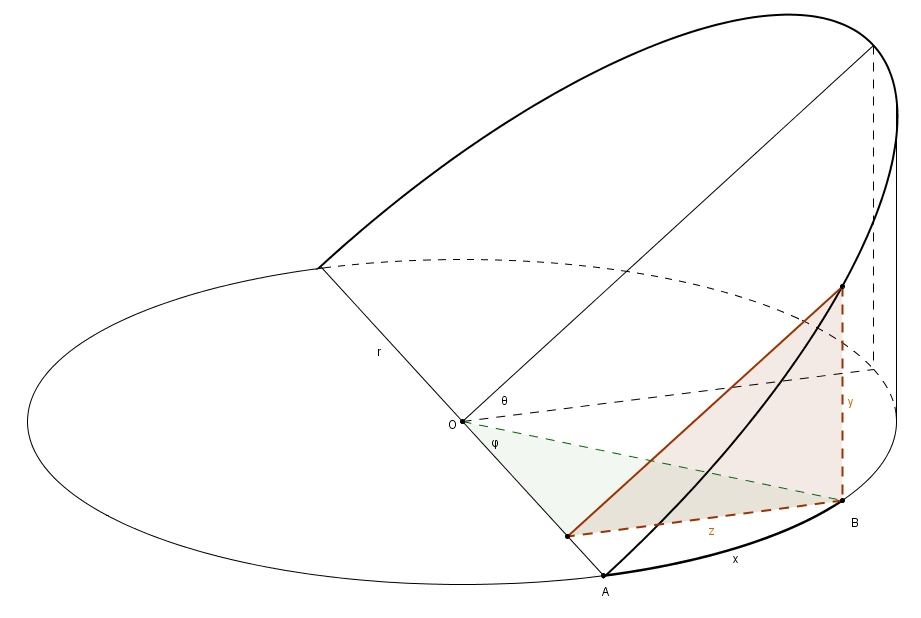
En se rappelant qu’un angle exprimé en radian correspond au rapport de l’arc de cercle intercepté et du rayon, on peut exprimer facilement la mesure de l’angle \(\varphi\) dans le triangle vert \[\varphi = \frac{x}{r}\]Cela nous permet aussi de trouver la mesure de la cathète \(z\) du triangle, \[z=r\sin\left(\frac{x}{r}\right)\]En considérant le triangle orange, on peut exprimer la mesure de \(y\) \[\tan(\theta) = \frac{y}{z} \ \ \Rightarrow \ \ \tan(\theta)=\frac{y}{r\sin\left(\frac{x}{r}\right)} \ \ \Rightarrow \ \ y = r\tan(\theta)\sin\left(\frac{x}{r}\right)\]Or comme \(r\) et \(\theta\) sont des constantes pour un cylindre et un plan donnés, \(y\) est une fonction de \(x\), une fonction sinusoïdale dont l’amplitude est \(r\tan(\theta)\) et la période est \(2\pi r\). Pour un rayon \(r\) fixe, l’amplitude du sinusoïde augmente donc lorsque l’angle \(\theta\) augmente.
L’arche sous l’axe des \(x\) de la fonction sinus (c’est-à-dire la deuxième partie de sa période) provient d’un second cylindrical wedge symétrique « sous » le cylindre.
Références :
Tom M. Apostol et Mamikon A. Mnatsakanian, Unwrapping curves from cylinders and cones, American Mathematical Monthly, 114 (2007), 388-416
L.R. King, An ellipse morphs to a cosine graph, The College Mathematics Journal, 44 (2013), 117- 123