Après la suite de Fibonacci, on fouille et cherche dans le triangle de Pascal dans l’espoir d’y trouver un autre résultat étonnant.

Les mathématiciens sont familiers depuis longtemps avec le fait que la \(n\)e ligne du triangle se somme à \(2^{n}\) (la première ligne étant commodément notée \(n=0\)). \[\sum_{k=0}^{n}\binom{n}{k}=\ 2^{n}\]Pour une preuve ingénieuse utilisant la combinatoire, on peut se référer à Andrews [1]. Qu’advient-il alors lorsqu’on multiplie les membres des lignes et donc qu’on s’intéresse à \[p_{n}= \prod_{k=0}^{n}\binom{n}{k}\]De prime abord, hélas, pas grand chose…
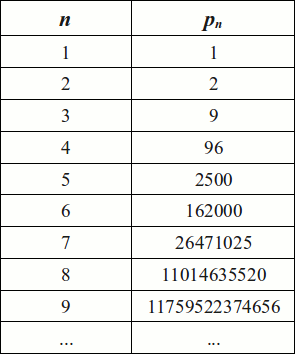
… outre que les valeurs successives de \(p_{n}\) croient très rapidement. Il serait donc peut-être pertinent de regarder du côté des rapports \(\dfrac{p_{n}}{p_{n-1}}\).
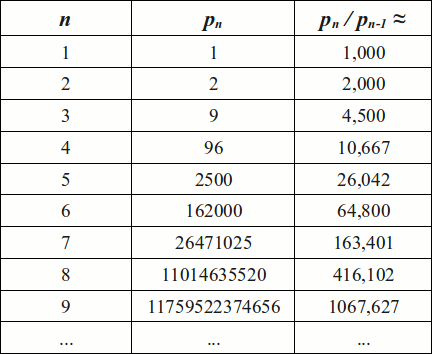
Même les rapports successifs croient eux-aussi de manière fulgurante ! Or il semble cette fois-ci qu’un lien multiplicatif approximatif lie les rapports successifs : pour les premières valeurs de \(n\), cela semble être un peu plus que le double ! Il nous reste donc à vérifier du côté des rapports des rapports.
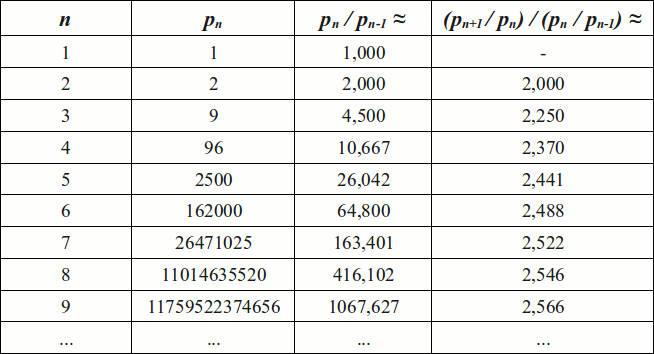
On s’intéresse à la valeur limite, si elle existe, de ces rapports de rapports. On trouve d’abord une expression pour \(p_{n}\) \begin{align*}p_{n} &= \prod_{k=0}^{n} \binom{n}{k} \\ \\ &=\frac{n!}{0!(n-0)!} \cdot \frac{n!}{1!(n-1)!} \ \cdot \ \dots \ \cdot \ \frac{n!}{(n-1)!(n-(n-1))!}\cdot \frac{n!}{n!(n-n)!}\end{align*}Au numérateur, on multiplie \(n!\) un total de \((n+1)\) fois. Au dénominateur, on remarque qu’on a deux fois les facteurs \(0!\), deux fois les facteurs \(1!\), … , deux fois les facteurs \((n-1)!\) et enfin deux fois les facteurs \(n!\). On obtient donc \[p_{n} = \left(n!\right)^{n+1}\cdot \prod_{k=0}^{n}\frac{1}{\left(k!\right)^{2}}\]On s’intéresse ensuite aux rapport \(\dfrac{p_{n}}{p_{n-1}}\) \[\frac{p_{n}}{p_{n-1}} = \frac{\left(n!\right)^{n+1}\cdot \prod_{k=0}^{n}\frac{1}{\left(k!\right)^{2}}}{\left(\left(n-1\right)!\right)^{(n-1)+1}\cdot \prod_{k=0}^{n-1}\frac{1}{\left(k!\right)^{2}}}\]qu’on simplie dans les étapes suivantes (en commençant par les produits peu commodes) qu’on espère suffisamment simples pour qu’elles se passent d’explication\begin{align*}\frac{p_{n}}{p_{n-1}}&=\frac{\left(n!\right)^{n+1}\cdot \prod_{k=0}^{n}\frac{1}{\left(k!\right)^{2}}}{\left(\left(n-1\right)!\right)^{n}\cdot \prod_{k=0}^{n}\frac{1}{\left(k!\right)^{2}}} \\ \\ &=\frac{\left(n!\right)^{n+1}\cdot \frac{1}{\left(n!\right)^{2}}\cdot \prod_{k=0}^{n-1}\frac{1}{\left(k!\right)^{2}}}{\left(\left(n-1\right)!\right)^{n}\cdot \prod_{k=0}^{n-1}\frac{1}{\left(k!\right)^{2}}} \\ \\ &=\frac{\left(n!\right)^{n+1}}{\left(\left(n-1\right)!\right)^{n} \cdot \left(n!\right)^{2}} \\ \\ &=\frac{\left(n!\right)^{n}}{\left(\left(n-1\right)!\right)^{n}\cdot n!}\\ \\ &=\frac{\left(n\left(n-1\right)!\right)^{n}}{\left(\left(n-1\right)!\right)^{n}\cdot n!} \\ \\ &=\frac{n^{n}\left(\left(n-1\right)!\right)^{n}}{\left(\left(n-1\right)!\right)^{n}\cdot n!}\\ \\ &=\frac{n^{n}}{n!}\end{align*}Pas si mal ! On s’intéresse enfin aux rapports des rapports qu’on simplifie eux-aussi étape par étape\begin{align*}\frac{p_{n+1}/p_{n}}{p_{n}/p_{n-1}}&= \frac{\frac{\left(n+1\right)^{n+1}}{\left(n+1\right)!}}{\frac{n^{n}}{n!}} \\ \\ &=\frac{\left(n+1\right)^{n+1}}{\left(n+1\right)!}\cdot \frac{n!}{n^{n}} \\ \\ &=\frac{\left(n+1\right)^{n}\cdot \left(n+1\right)\cdot n!}{n^{n} \cdot \left(n+1\right)\cdot n!} \\ \\ &=\frac{\left(n+1\right)^{n}}{n^{n}}\\ \\ &=\left(\frac{n+1}{n}\right)^{n}\\ \\ &=\left(1 + \frac{1}{n}\right)^{n}\end{align*}Et là comme \[\lim_{n\to \infty}\left(1 + \frac{1}{n}\right)^{n}=e\]on trouve que\[\lim_{n\to \infty} \frac{\phantom{x}\frac{p_{n+1}}{p_{n}}\phantom{x}}{\frac{p_{n}}{p_{n-1}}} =e\]c’est-à-dire que lorsque \(n\to \infty\), les rapports des rapports tendent vers le nombre \(e\).
[1] George E. Andrews (1994), Number Theory
Référence : Harlan J. Brothers, Mathematics Magazine, Volume 85, Number 1, February 2012 , pp. 51-51(1)