Voici une petite construction facile et intéressante à réaliser. Sur une feuille de papier tracez un cercle et découpez-le.
Identifier trois points sur la circonférence du cercle. Faites en sorte que les points puissent former un triangle acutangle

de telle sorte que
Rabattez ensuite deux des côtés du triangle et notez le point d’intersection des arcs de cercles.
puis rabattez ensuite le troisième côté…
Dépliez. Le point d’intersection correspond à l’orthocentre, le point d’intersection des trois hauteurs.
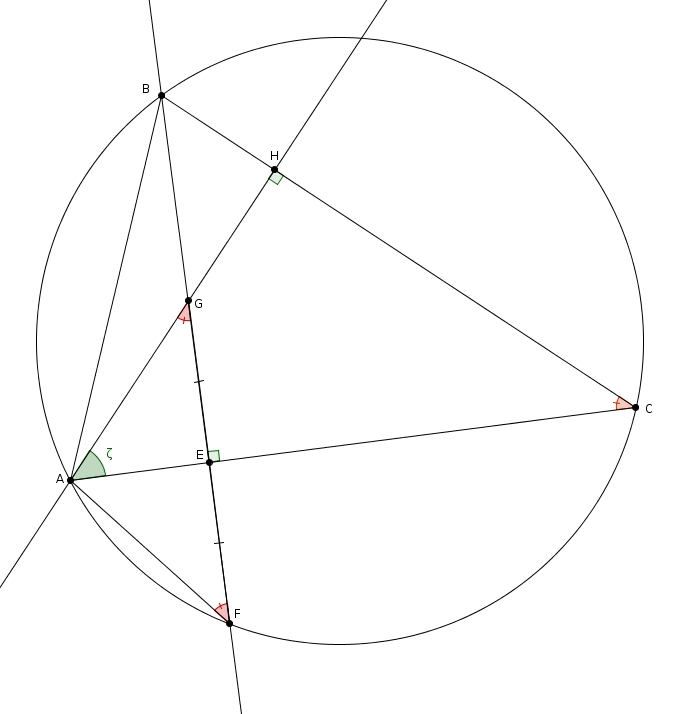
Ah ! Et maintenant, pourquoi ça marche ? Cela ne m’apparaissait pas nécessairement évident de prime abord, mais il suffit de regarder les bons angles dans les bons triangles (comme d’habitude !) Considérons le triangle ABC dans le cercle suivant. J’ai tracé les hauteurs AH et BE qui se rencontrent en G.
 Il faut montrer que
Il faut montrer que
![]()
Les angles AFB et ACB sont isométriques puisque ce sont des angles inscrits qui interceptent le même arc. Moins évident est le fait que l’angle AGF est aussi isométrique à l’angle ACB. Les triangles GAE et CAH sont tous deux rectangles (par définition de hauteur). Ces deux triangles partagent aussi l’angle GAE (noté ζ sur le schéma). Ils sont donc semblables par le cas AA. Et comme dans les triangles semblables les angles homologues sont isométriques, cela implique que l’angle AGE est isométrique à l’angle ACH.
Le triangle AGF est donc isocèle. AE est une hauteur du triangle isocèle. Or, dans un triangle isocèle, cette hauteur est aussi médiatrice (entre autres). Et par définition de médiatrice, on obtient le résultat recherché.
Référence : Orthocenter Curiosities sur “I hope this old train breaks down…”





superbe !
Le genre de propriété belle , manipulable et riche de questions .
Bonjour !
Je viens de découvrir votre site ! Une vraie mine d’or.
Par ailleurs, je viens de relire ce billet et j’y ai trouvé une coquille.
Bonne journée !