Pôles, polaires et coniques…

J’avais le goût de faire des gifs animés dans Géogébra alors voici mon excuse.

L’inversion

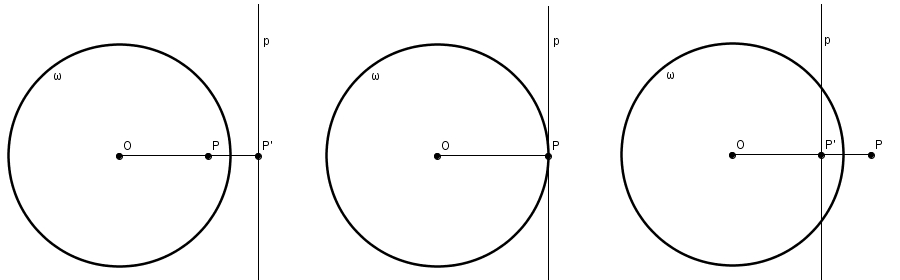
On s’intéresse d’abord d’une manière quelque peu superficielle à l’inversion, une transformation néanmoins fort intéressante du plan, décrite entre autre par le grand géomètre suisse Jakob Steiner en 1824. D’un cercle \(\omega\) de centre \(O\) et de rayon \(k\), on définit l’inverse d’un point \(P\) du plan (autre que \(O\)) comme le point \(P^{\prime}\) sur la demi-droite \(OP\) et pour lequel on observe la relation suivante \[m\overline{OP}\cdot m\overline{OP^{\prime}} = k^{2}\]Il se trouve selon cette définition que l’inverse de \(P^{\prime}\) est \(P\). L’inversion est donc involutive (elle est sa propre réciproque). Il est aussi facile de voir que chaque point à l’extérieur du cercle est envoyé à l’intérieur du cercle et chaque point à l’intérieur du cercle (sauf le centre \(O\)) est envoyé à l’extérieur du cercle. Les points sur le cercle sont bien sûr invariants. On peut construire l’inverse d’un point \(P\) à l’intérieur du cercle d’inversion. On cherche \(T\), l’extrémité d’une corde passant par \(P\) et perpendiculaire à la demi-droite \(OP\). La tangente au cercle \(\omega\) passant par \(T\) rencontre la demi-droite \(OP\) en \(P^{\prime}\) et c’est le point recherché !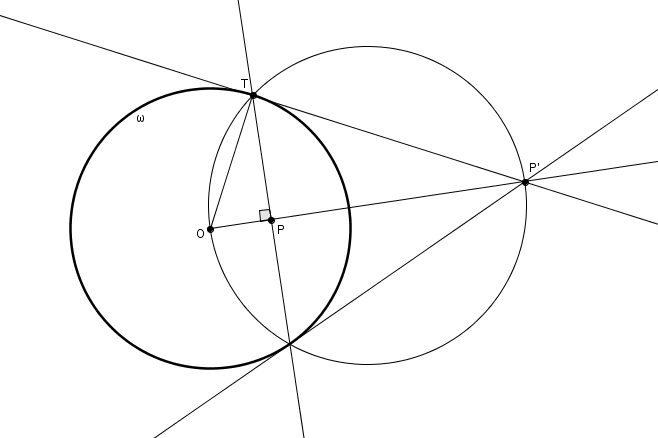En effet, le triangle \(OTP^{\prime}\) étant rectangle (la tangente rencontre perpendiculairement le rayon \(OT\)) et puisque les triangles rectangles \(OPT\) et \(OTP^{\prime}\) sont semblables par le cas de similitude AA, et que la mesure de \(OT\) est égale à celle du rayon \(k\), on a bien \[\frac{m\overline{OP}}{k} =\frac{k}{m\overline{OP^{\prime}}}\]Cette méthode nous permet aussi de trouver l’inverse d’un point \(P\) si \(P\) est à l’extérieur du cercle. On trace la demi-droite \(OP\) et l’une des deux tangentes au cercle passant par \(P\). Cette tangente touche le cercle en \(T\). Le point recherché \(P^{\prime}\) est le pied de la perpendiculaire à \(OP\) passant par \(T\).

Il existe bien sûr d’autres moyens de trouver \(P^{\prime}\) (en particulier si \(m\overline{OP}>\frac{1}{2}k\) il est possible d’utiliser le compas seul) mais cela n’est pas l’objet du présent billet. On note tout de même avant de continuer que l’inversion est une transformation fascinante : qu’advient-il lorsqu’on inverse une droite passant par \(O\) ? Ne passant pas par \(O\) ? D’un cercle passant par \(O\) ? Ne passant pas par \(O\) ? D’un triangle ? etc. Les résultats sont parfois surprenants et mériteront qu’on s’y attarde dans un futur billet. L’inversion est aussi souvent une première occasion d’étendre le plan euclidien « régulier ». Dans ce cas-ci, on étend le plan euclidien avec un point « idéal » à l’infini \(O^{\prime}\), image de \(O\), centre du cercle d’inversion.

L’inversion est en outre très différente des translations, rotations ou réflexions et des homothéties mais elle partage entre autres avec ces transformations du plan la caractéristique élémentaire qu’elle transforme des points en points. Cela n’est pas le cas avec la prochaine transformation, qui entretient cependant un étroit lien avec l’inversion.

Les pôles et polaires

Dans cette transformation (reciprocation en anglais), les points sont transformés en droites et les droites en points. Pour cette variante de l’inversion, on utilise un cercle \(\omega\) de centre \(O\) et de rayon \(k\). Chaque point \(P\) (autre que \(O\)) détermine une droite \(p\), appelée la polaire de \(P\), qui est la droite perpendiculaire à \(OP\) passant par l’inverse \(P^{\prime}\) de \(P\). Au contraire, toute droite \(p\) (ne passant pas par \(O\)) détermine un point \(P\), appelé le pôle de \(p\), qui est l’inverse du pied de la perpendiculaire joignant \(O\) à \(p\). La polaire d’un point sur le cercle d’inversion est la tangente au cercle en ce point et le pôle d’une tangente au cercle d’inversion est le point de tangence. Dans aucun autre cas une polaire passe-t-elle par son pôle.

Les coniques

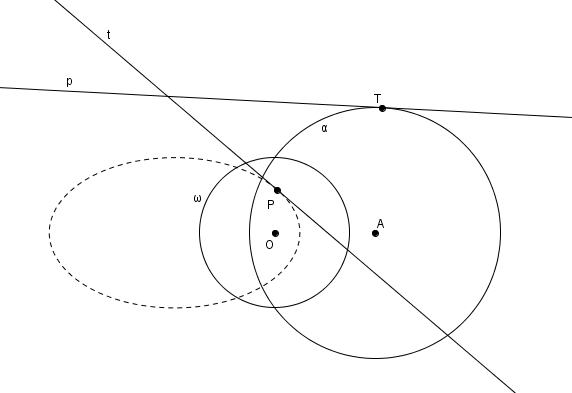
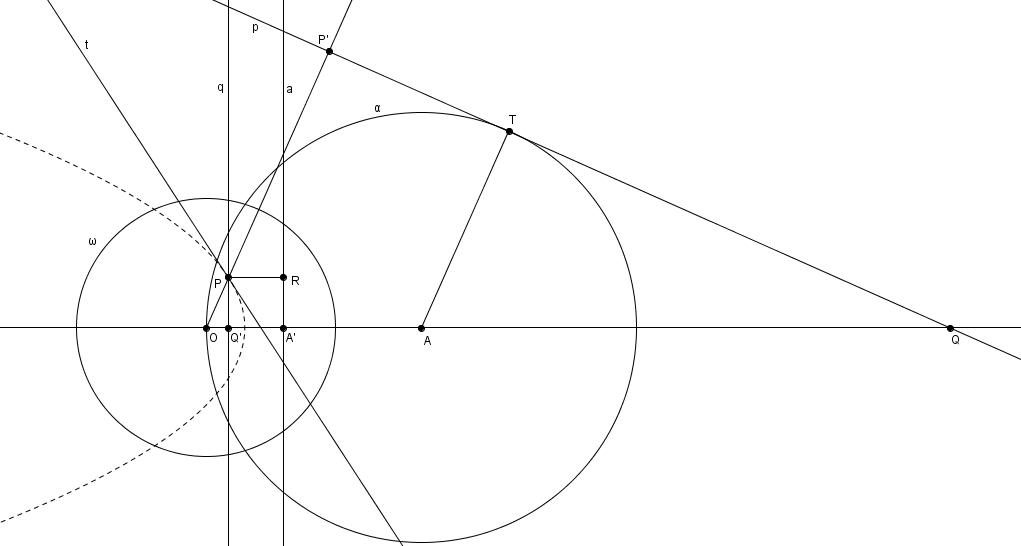
Voici comment il est possible de définir les coniques à l’aide des pôles et polaires. On considère un cercle \(\omega\) de centre \(O\) et de rayon \(k\), et un autre cercle \(\alpha\) de centre \(A\) et de rayon \(r\). Les coniques peuvent être définies par rapport à \(\omega\) à la fois comme un lieu de points, en considérant les pôles \(P\) des tangente \(p\) à \(\alpha\), et à la fois comme une enveloppe de droites, en considérant les polaires \(t\) des points \(T\) sur \(\alpha\). Le rayon \(k\) de \(\omega\) n’affecte pas la forme de la conique mais seulement ses dimensions. En outre, la forme de la conique est déterminée par le rapport\[\epsilon = \frac{m\overline{OA}}{r}\]qu’on appelle excentricité de la conique. Si \[\epsilon = \frac{m\overline{OA}}{r}<1\]c’est-à-dire si \(O\) se trouve à l’intérieur de \(\alpha\), on obtient une figure ovale : l’ellipse. Plus \(\epsilon\) s’approche de \(0\), plus l’ellipse s’apparente à un cercle (à la limite, lorsque \(O\) et \(A\) coïncident, on a \(\epsilon = 0\) et l’image de \(\alpha\) est un cercle) et, au contraire, plus \(\epsilon\) s’approche de \(1\), moins la figure s’apparente à un cercle.

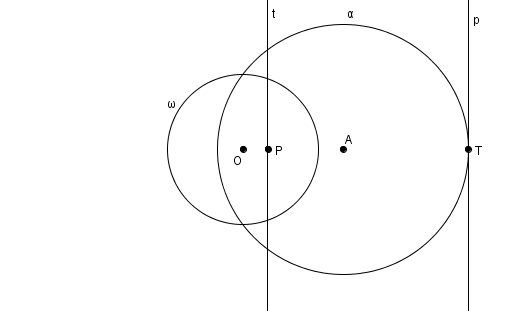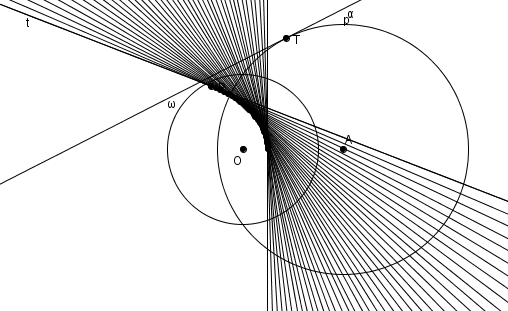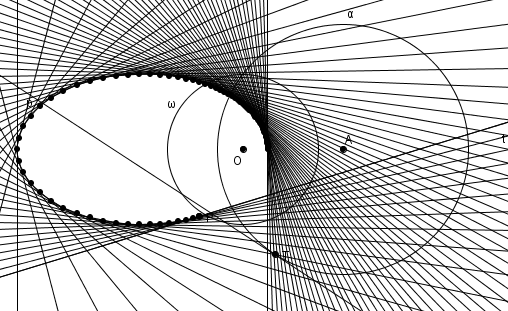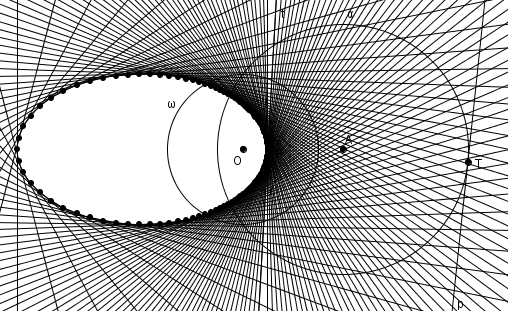L’ellipse à la fois comme enveloppe de polaires et lieu de pôles

Si \[\epsilon = \frac{m\overline{OA}}{r} = 1\]c’est-à-dire si \(O\) est sur \(\alpha\), alors on a un point, le point \(O\) sur \(\alpha\), qui n’a pas de polaire et une tangente, la tangente à \(\alpha\) en \(O\), qui n’a pas de pôle : on obtient une parabole et elle s’étend à l’infini en direction \(AO\).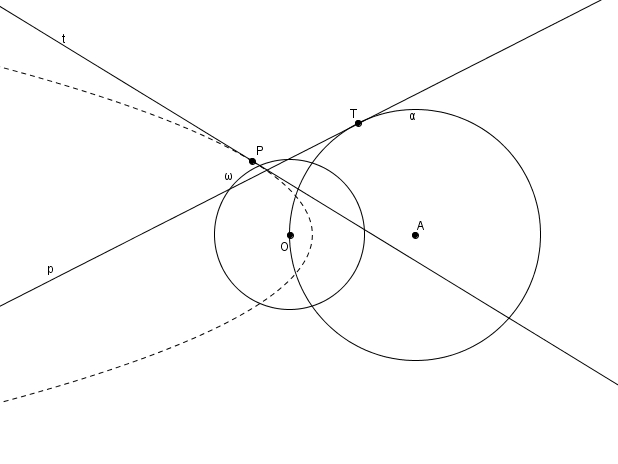

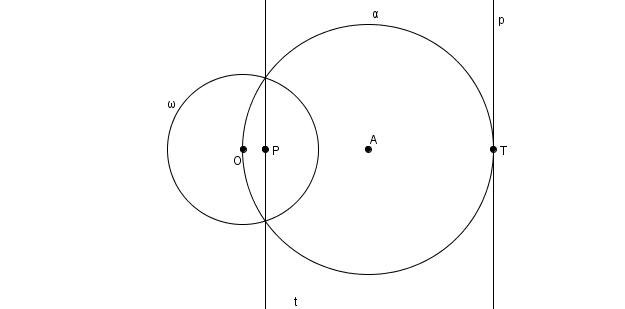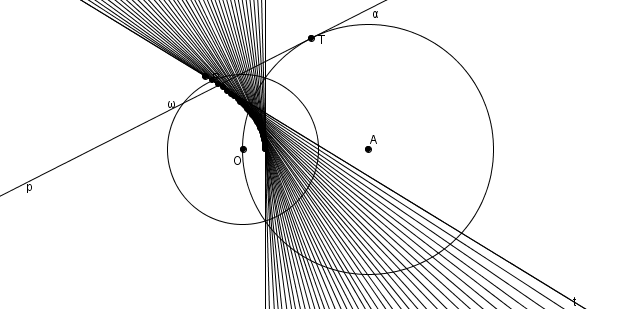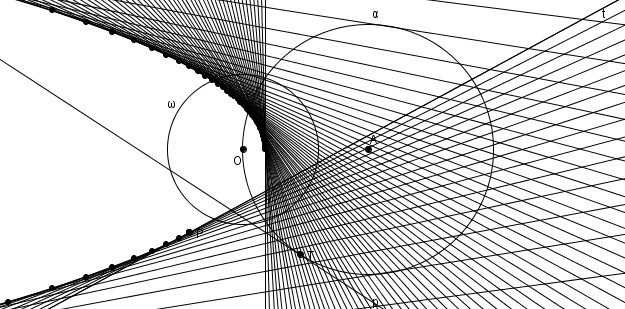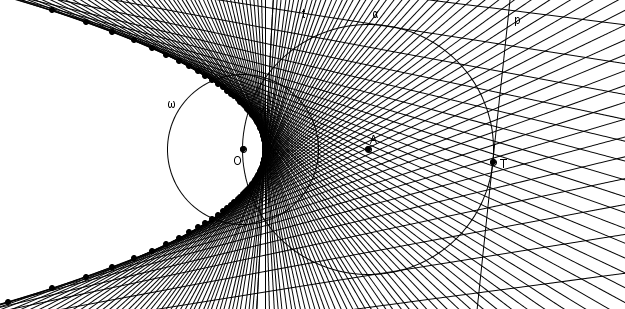
La parabole à la fois comme enveloppe de polaires et lieu de pôles

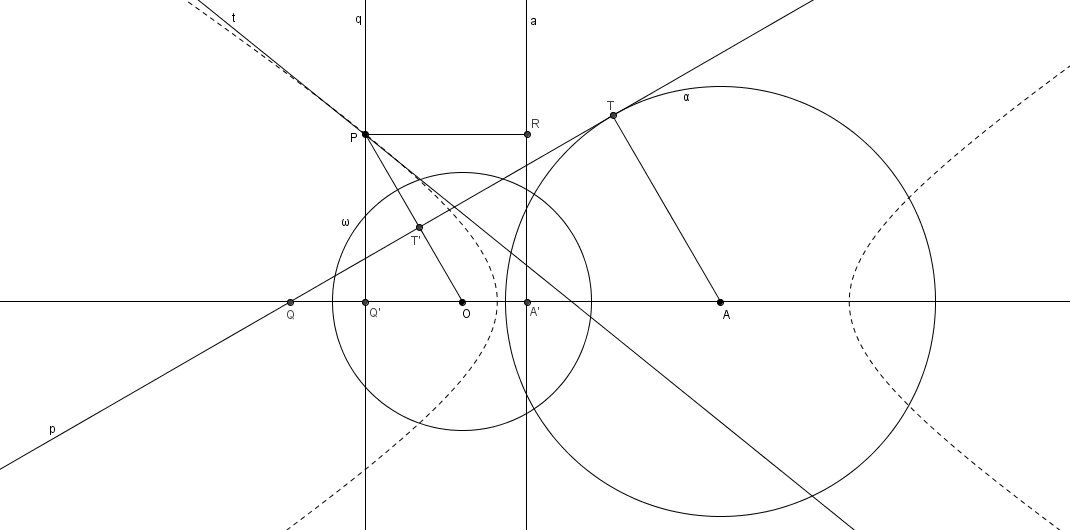
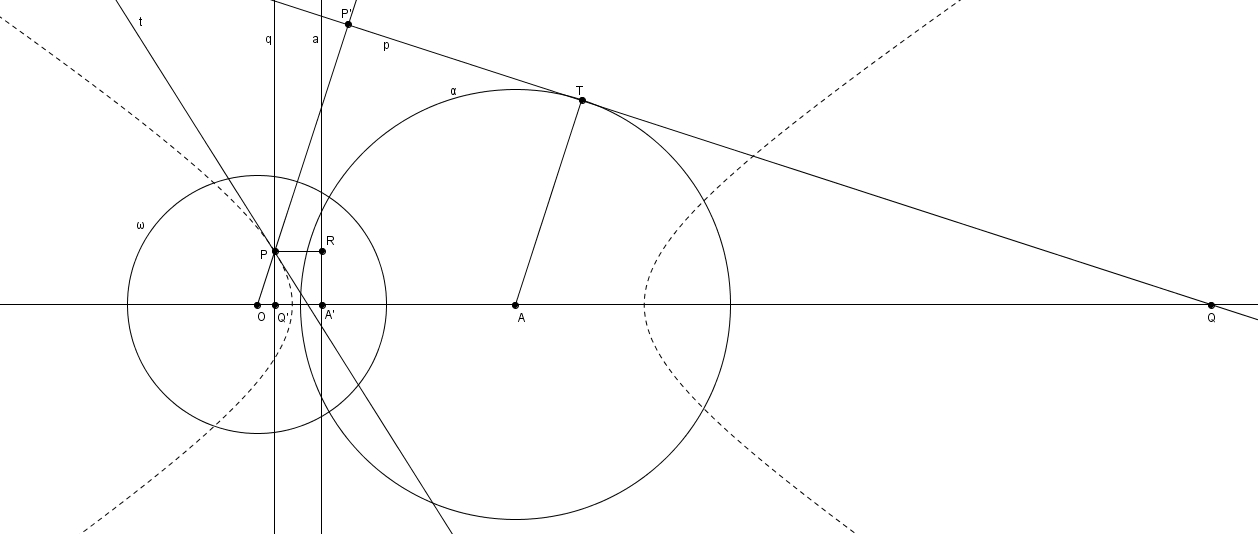
Enfin, si\[\epsilon=\frac{m\overline{OA}}{r}>1\]c’est-à-dire si \(O\) est à l’extérieur de \(\alpha\), alors on a deux tangentes à \(\alpha\), les deux tangentes passant par \(O\), qui n’ont pas de pôle ; cependant les points de tangence de ces tangentes possèdent bel et bien des polaires : ces polaires sont les asymptotes de la courbe obtenue : l’hyperbole.

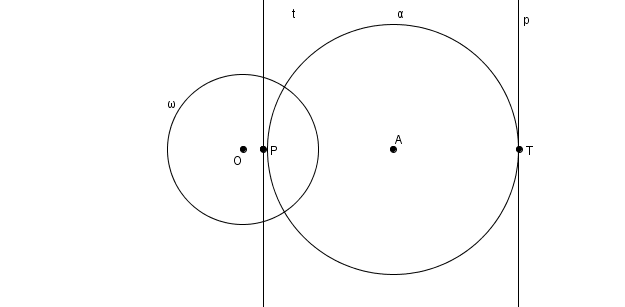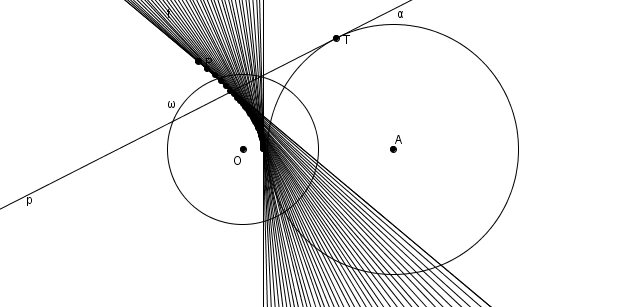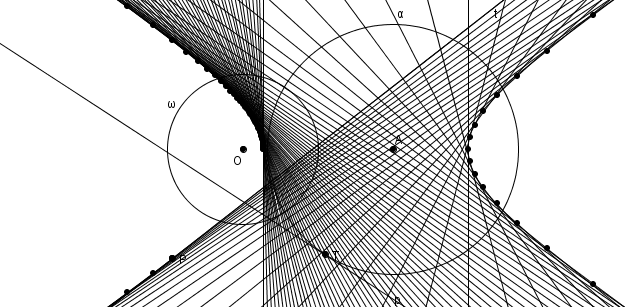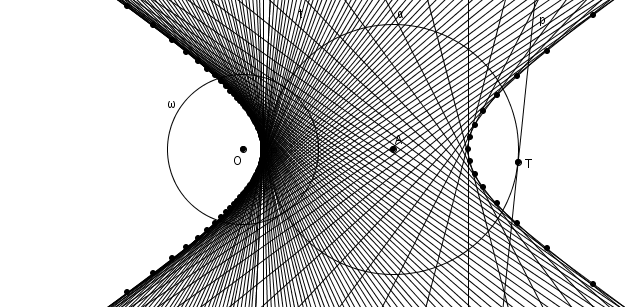L’hyperbole à la fois comme enveloppe de polaires et lieu de pôles

En terminant, il est possible de raccorder ces définitions des coniques avec celles plus classiques d’un foyer et d’une directrice. On appelle \(O\) le foyer de la conique, \(A\) son centre et la polaire \(a\) de \(A\) sa droite directrice. On peut vérifier que pour un point \(P\) sur la conique on a bien que la mesure de \(\overline{OP}\), appelée distance focale, est égale à \(\epsilon\) fois la distance de \(P\) à la directrice \(a\).

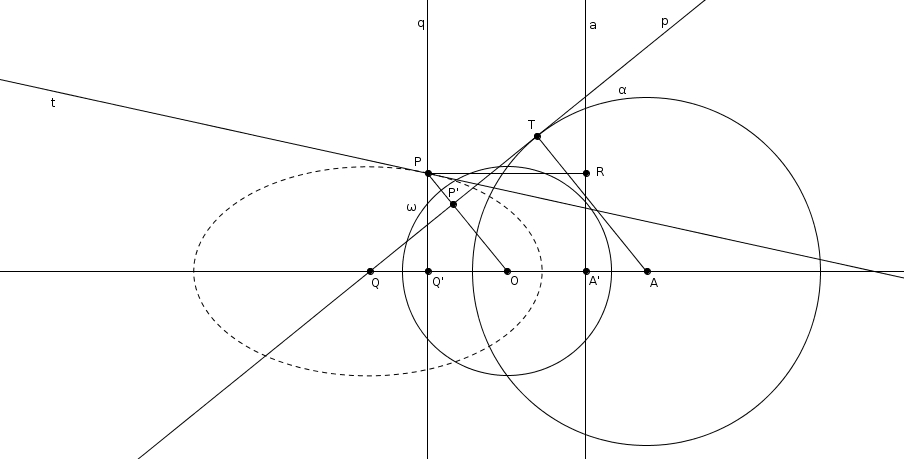
Le point \(P\) est le pôle (par rapport au cercle d’inversion \(\omega\)) d’une tangente \(p\) à \(\alpha\) (en \(T\)) qui coupe \(OA\) en \(Q\) et rencontre \(OP\) en \(P^{\prime}\) (l’inverse de \(P\)). La droite directrice \(a\), polaire de \(A\), et la polaire de \(Q\) (notée \(q\)) rencontrent respectivement \(OA\) en \(A^{\prime}\) (l’inverse de \(A\)) et \(Q^{\prime}\) (l’inverse de \(Q\)). On note \(R\) le pied de la perpendiculaire à \(a\) par \(P\). On doit prouver que \[m\overline{OP} = \epsilon \cdot m\overline{PR}\]Si \(Q^{\prime}\) est à gauche de \(O\)

 on a \[\frac{m\overline{PR}}{m\overline{OP}} = \frac{m\overline{OA^{\prime}}+m\overline{OQ^{\prime}}}{m\overline{OP}}\]ce qui est équivalent en multipliant par \(\frac{k}{k}\) à \[\frac{m\overline{OA^{\prime}}+m\overline{OQ^{\prime}}}{m\overline{OP}} = \frac{k}{m\overline{OP}}\left(\frac{m\overline{OA^{\prime}}}{k}+\frac{m\overline{OQ^{\prime}}}{k}\right)\]Or comme \[m\overline{OP}\cdot m\overline{OP^{\prime}}=k^{2}\]on trouve\[\frac{k}{m\overline{OP}}=\frac{m\overline{OP^{\prime}}}{k}\]et on obtient des expressions équivalentes pour \(\overline{OA^{\prime}}\) \[\frac{k}{m\overline{OA}} = \frac{m\overline{OA^{\prime}}}{k}\]et \(\overline{OQ^{\prime}}\) \[\frac{k}{m\overline{OQ}}=\frac{m\overline{OQ^{\prime}}}{k}\]En remplaçant on obtient \[\frac{k}{m\overline{OP}}\left(\frac{m\overline{OA^{\prime}}}{k}+\frac{m\overline{OQ^{\prime}}}{k}\right) = \frac{m\overline{OP^{\prime}}}{k}\left(\frac{k}{m\overline{OA}}+\frac{k}{m\overline{OQ}}\right)\]ou de manière équivalente\[\frac{m\overline{OP^{\prime}}}{k}\left(\frac{k}{m\overline{OA}}+\frac{k}{m\overline{OQ}}\right)=\frac{m\overline{OP^{\prime}}}{1}\left(\frac{1}{m\overline{OA}}+\frac{1}{m\overline{OQ}}\right)\]Après une mise en évidence de \(\frac{1}{m\overline{OQ}}\), on a \[\frac{m\overline{OP^{\prime}}}{1}\left(\frac{1}{m\overline{OA}}+\frac{1}{m\overline{OQ}}\right)=\frac{m\overline{OP^{\prime}}}{m\overline{OQ}}\left(\frac{m\overline{OQ}}{m\overline{OA}}+\frac{m\overline{OQ}}{m\overline{OQ}}\right) = \frac{m\overline{OP^{\prime}}}{m\overline{OQ}}\left(\frac{m\overline{OQ}}{m\overline{OA}}+1\right)\]Or puisque \[\frac{m\overline{OP^{\prime}}}{m\overline{OQ}}=\frac{m\overline{AT}}{m\overline{AQ}}\]on obtient \[\frac{m\overline{OP^{\prime}}}{m\overline{OQ}}\left(\frac{m\overline{OQ}}{m\overline{OA}}+1\right)=\frac{m\overline{AT}}{m\overline{AQ}}\left(\frac{m\overline{OQ}}{m\overline{OA}}+1\right)\]puis \[\frac{m\overline{AT}}{m\overline{AQ}}\left(\frac{m\overline{OQ}}{m\overline{OA}}+1\right) = \frac{m\overline{AT}}{m\overline{AQ}}\left(\frac{m\overline{OQ}}{m\overline{OA}}+\frac{m\overline{OA}}{m\overline{OA}}\right) = \frac{m\overline{AT}}{m\overline{AQ}}\cdot \frac{m\overline{AQ}}{m\overline{OA}}\]puisque \[m\overline{OQ}+m\overline{OA}=m\overline{AQ}\]Enfin,\[\frac{m\overline{AT}}{m\overline{AQ}}\cdot \frac{m\overline{AQ}}{m\overline{OA}} = \frac{m\overline{AT}}{m\overline{OA}} = \frac{r}{m\overline{OA}} = \frac{1}{\epsilon}\]c’est-à-dire \[\frac{m\overline{OP}}{m\overline{PR}} = \epsilon\]Si \(Q^{\prime}\) est à droite de \(O\) (mais à gauche de \(A^{\prime}\))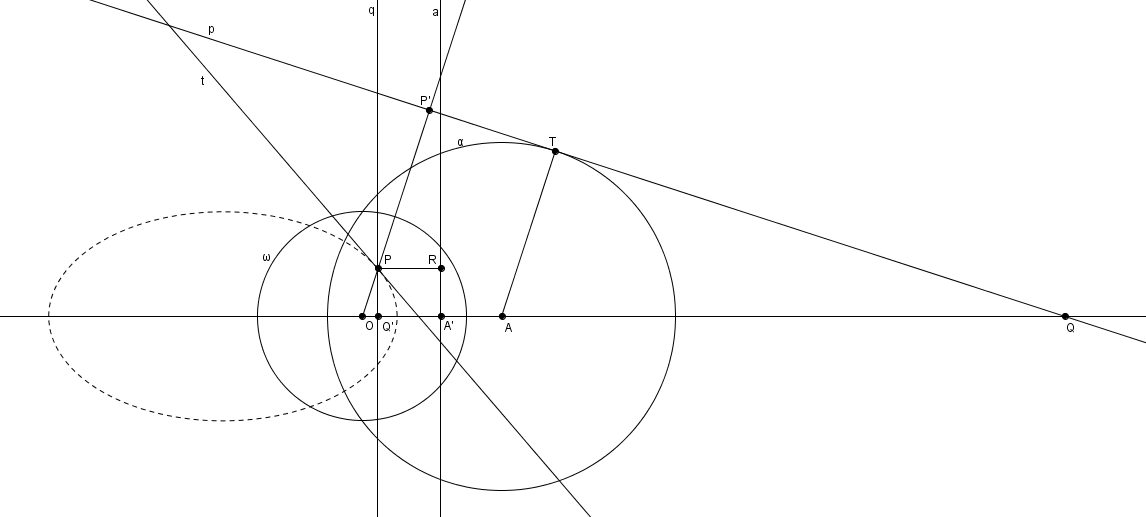il suffit d’ajuster un signe afin d’obtenir \begin{align*}\frac{m\overline{PR}}{m\overline{OP}}&=\frac{m\overline{OA^{\prime}}-m\overline{OQ^{\prime}}}{m\overline{OP}} \\ \\ &=\frac{k}{m\overline{OP}}\left(\frac{m\overline{OA^{\prime}}}{k}-\frac{m\overline{OQ^{\prime}}}{k}\right) \\ \\ &=\frac{m\overline{OP^{\prime}}}{k}\left(\frac{k}{m\overline{OA}}-\frac{k}{m\overline{OQ}}\right) \\ \\ &=\frac{m\overline{OP^{\prime}}}{1}\left(\frac{1}{m\overline{OA}}-\frac{1}{m\overline{OQ}}\right) \\ \\ &=\frac{m\overline{OP^{\prime}}}{m\overline{OQ}}\left(\frac{m\overline{OQ}}{m\overline{OA}}-1\right) \\ \\ &=\frac{m\overline{AT}}{m\overline{AQ}}\cdot \frac{m\overline{AQ}}{m\overline{OA}} \\ \\ &=\frac{r}{m\overline{OA}} \\ \\ &=\frac{1}{\epsilon}\end{align*}ou de manière équivalente \[\frac{m\overline{OP}}{m\overline{PR}} = \epsilon\]Ces distinctions peuvent s’accommoder d’une distance signée : dans ce cas, une seule démarche suffirait. Commodément, la démarche est la même avec la parabole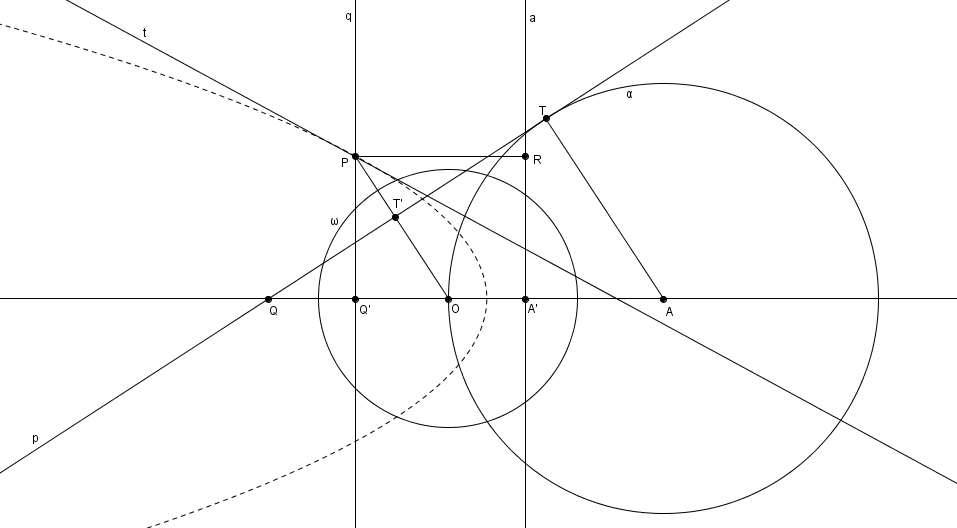

et avec l’hyperbole

Dans le cas de cette dernière, si en plus \(Q^{\prime}\) est à droite de \(A^{\prime}\),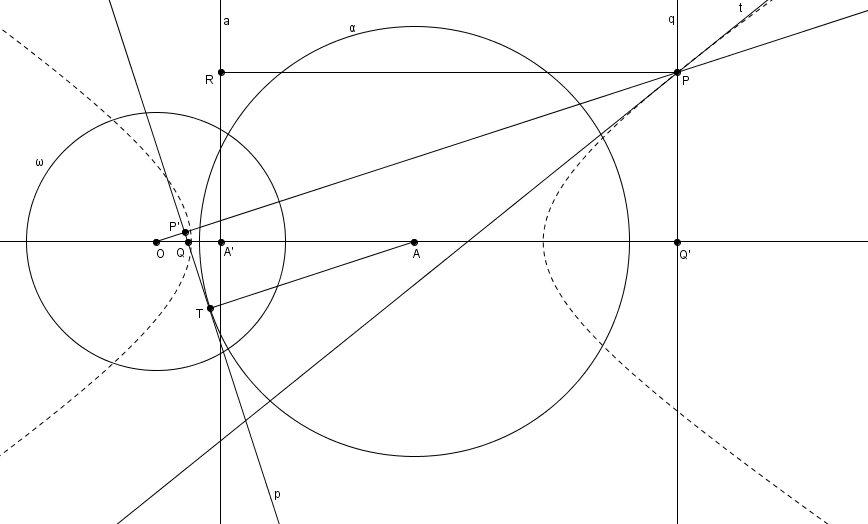

on a \begin{align*} \frac{m\overline{PR}}{m\overline{OP}} &= \frac{m\overline{OQ^{\prime}}-m\overline{OA^{\prime}}}{m\overline{OP}} \\ \\ &=\frac{k}{m\overline{OP}}\left(\frac{m\overline{OQ^{\prime}}}{k}-\frac{m\overline{OA^{\prime}}}{k}\right)\\ \\ &=\frac{m\overline{OP^{\prime}}}{k}\left(\frac{k}{m\overline{OQ}}-\frac{k}{m\overline{OA}}\right) \\ \\ &=\frac{m\overline{OP^{\prime}}}{m\overline{OQ}}\left(1-\frac{m\overline{OQ}}{m\overline{OA}}\right) \\ \\ &=\frac{m\overline{OP^{\prime}}}{m\overline{OQ}}\left(\frac{m\overline{OA}-m\overline{OQ}}{m\overline{OA}}\right) \\ \\ &=\frac{m\overline{OP^{\prime}}}{m\overline{OQ}}\cdot \frac{m\overline{AQ}}{m\overline{OA}}\\ \\ &=\frac{m\overline{AT}}{m\overline{AQ}}\cdot \frac{m\overline{AQ}}{m\overline{OA}}\\ \\ &=\frac{m\overline{AT}}{m\overline{OA}} \\ \\ &=\frac{r}{m\overline{OA}} \\ \\ &=\frac{1}{\epsilon}\end{align*}ce qui nous mène encore à la conclusion souhaitée \[\frac{m\overline{OP}}{m\overline{PR}} = \epsilon\]

Référence : H. S. M. Coxeter (1989), Introduction to Geometry (2nd Edition), Wiley

H. S. M. Coxeter et S. Greitzer (1967), Geometry Revisited, MAA Press

R. A. Johnson (2013), Advanced Euclidean Geometry, Dover