\(\displaystyle \sum_{i=1}^{\infty}\frac{1}{2^i} = 1\)
Alerte au divulgâcheur : vous avez peut-être déjà vu cette « preuve sans mot » de la somme des inverses des puissances de \(2\) ? C’est joli non ? Voici quelques animations réalisées dans Géogébra que je trouvais pas mal. Il y a même des séries alternées.
\(\displaystyle \sum_{i=1}^{\infty} \frac{1}{3^{i}} = \frac{1}{2}\)
\(\displaystyle \sum_{i=1}^{\infty}\frac{1}{4^{i}} = \frac{1}{3}\)
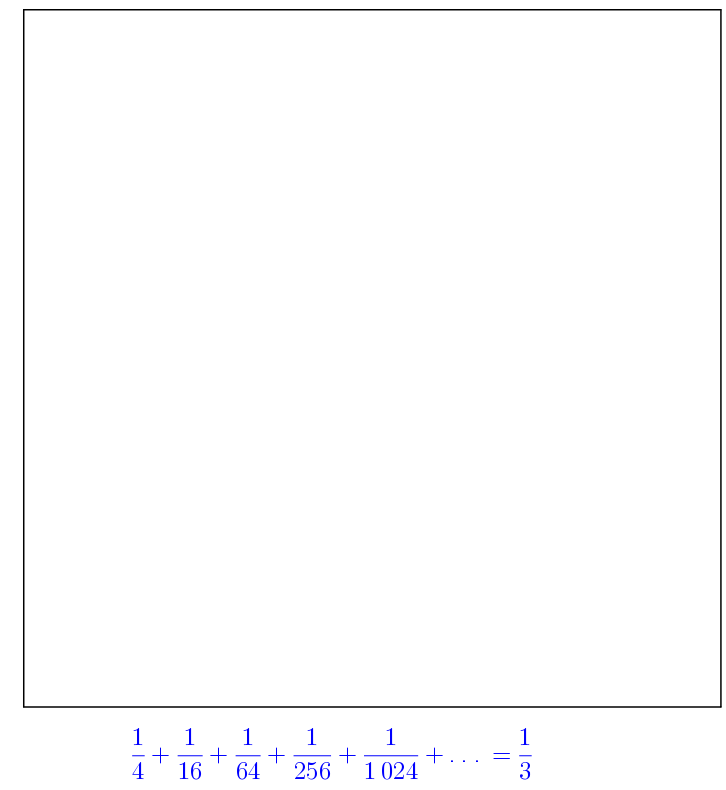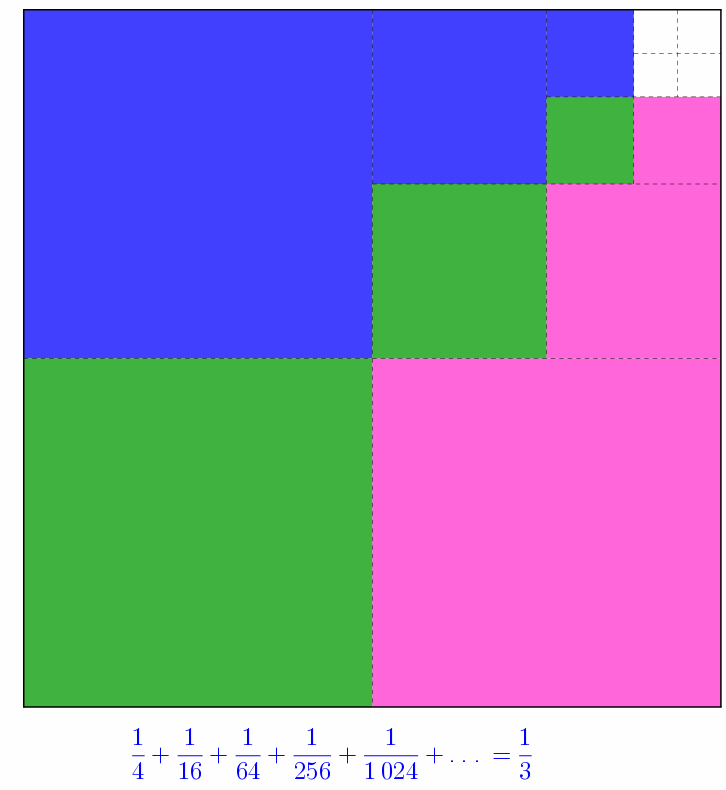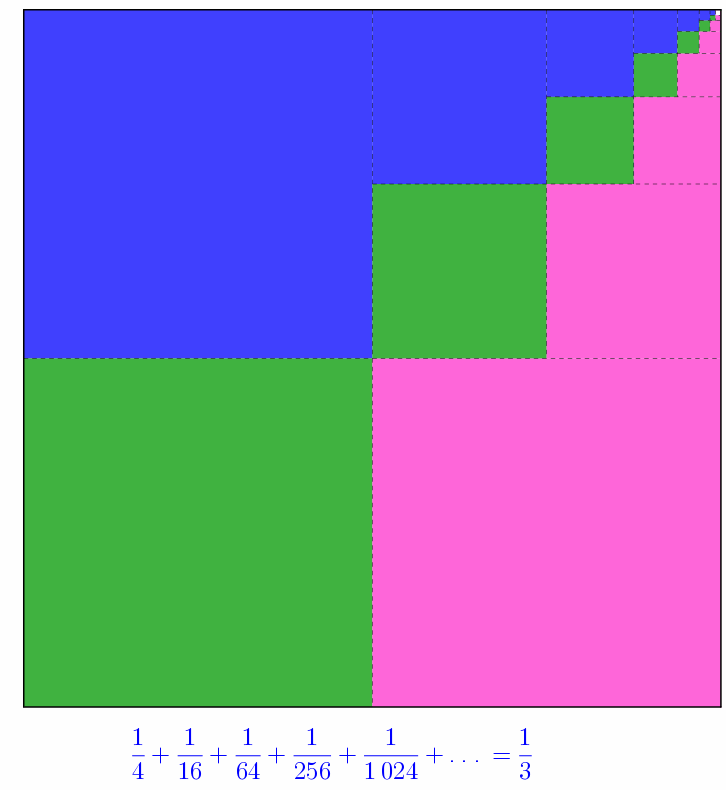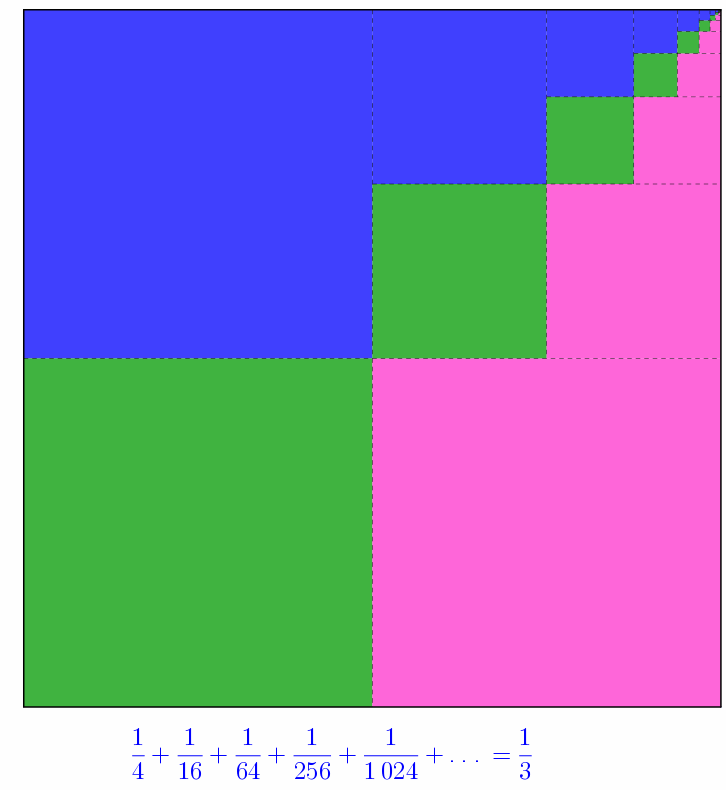
et plus généralement…
\(\displaystyle \sum_{i=1}^{\infty}\frac{1}{(1+n)^{i}} = \frac{1}{n}\)
si \(|n+1|>1\)
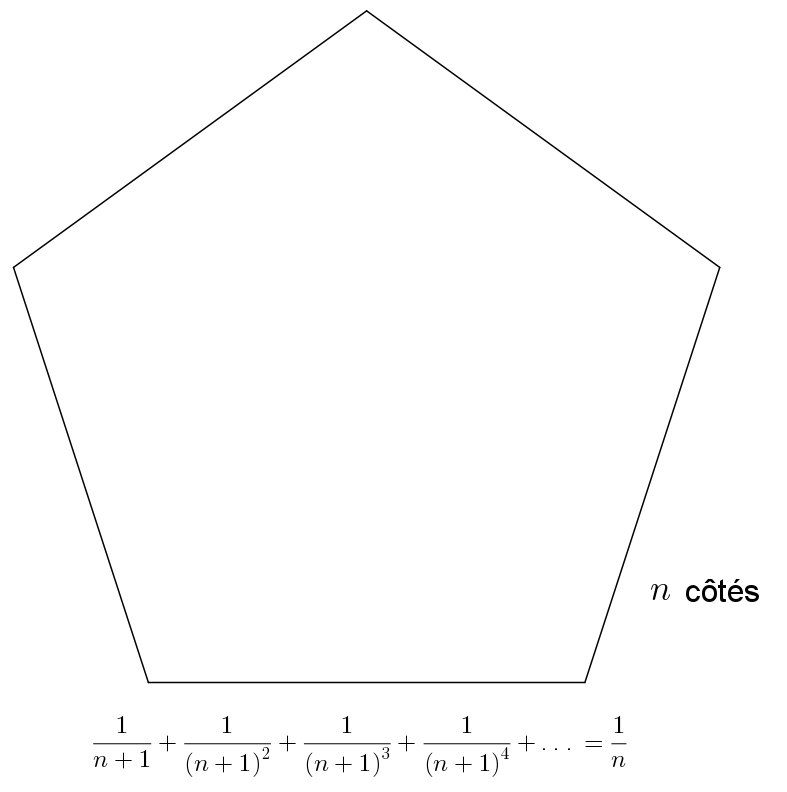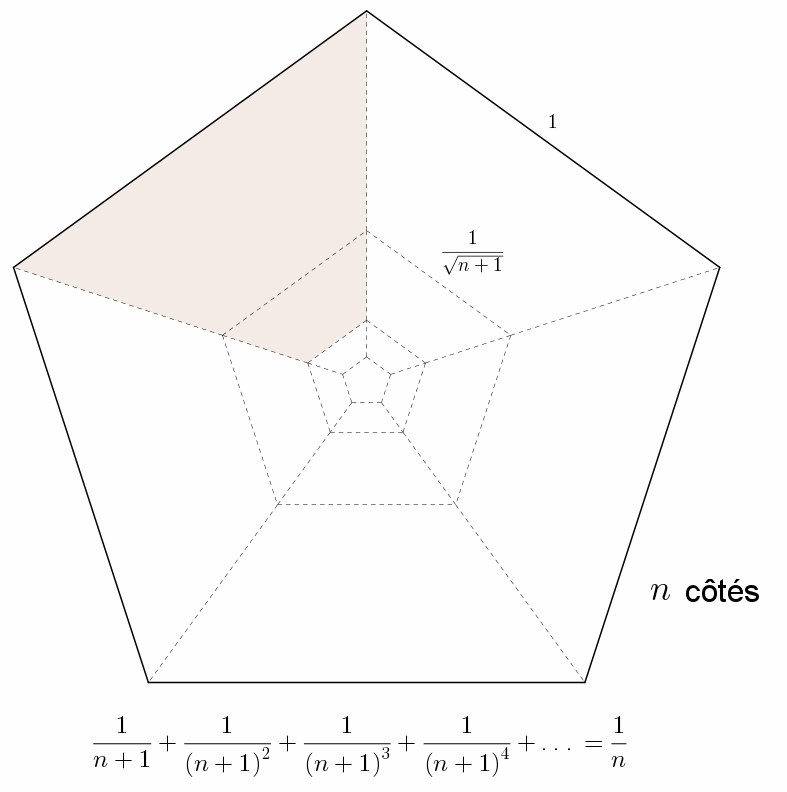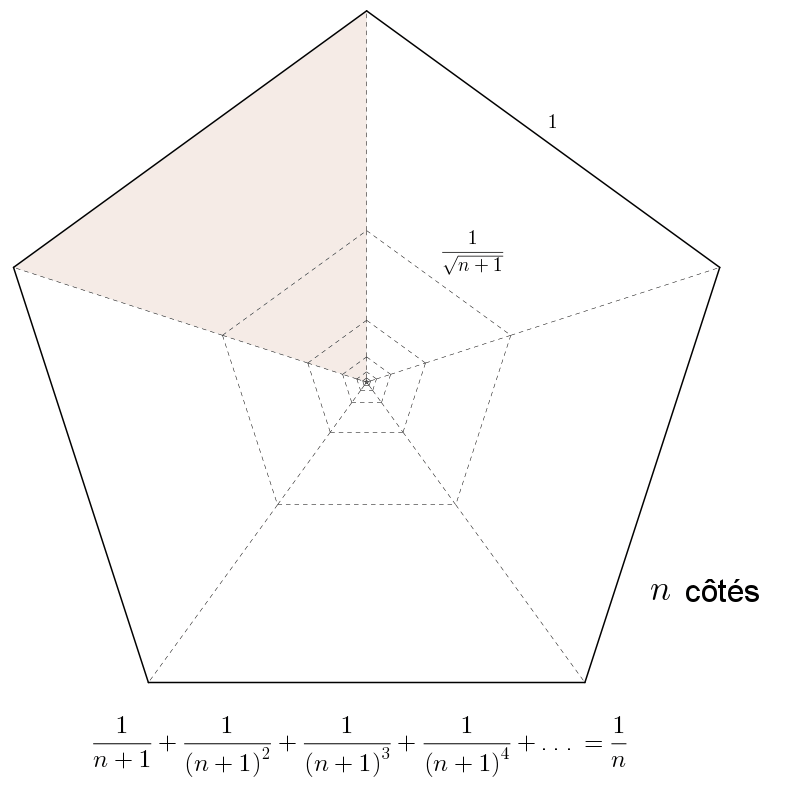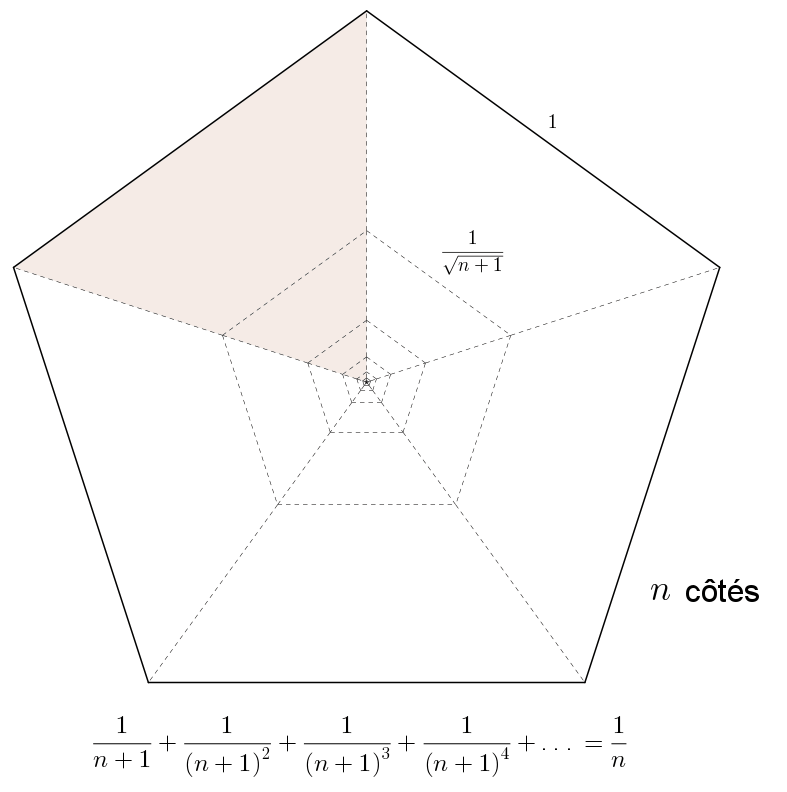Enfin, deux séries alternées.
\(\displaystyle \sum_{i=0}^{\infty} \frac{(-1)^{i}}{2^{i}} = \frac{2}{3}\)
\(\displaystyle \sum_{i=0}^{\infty}\frac{(-1)^{i}}{3^{i}} = \frac{3}{4}\)
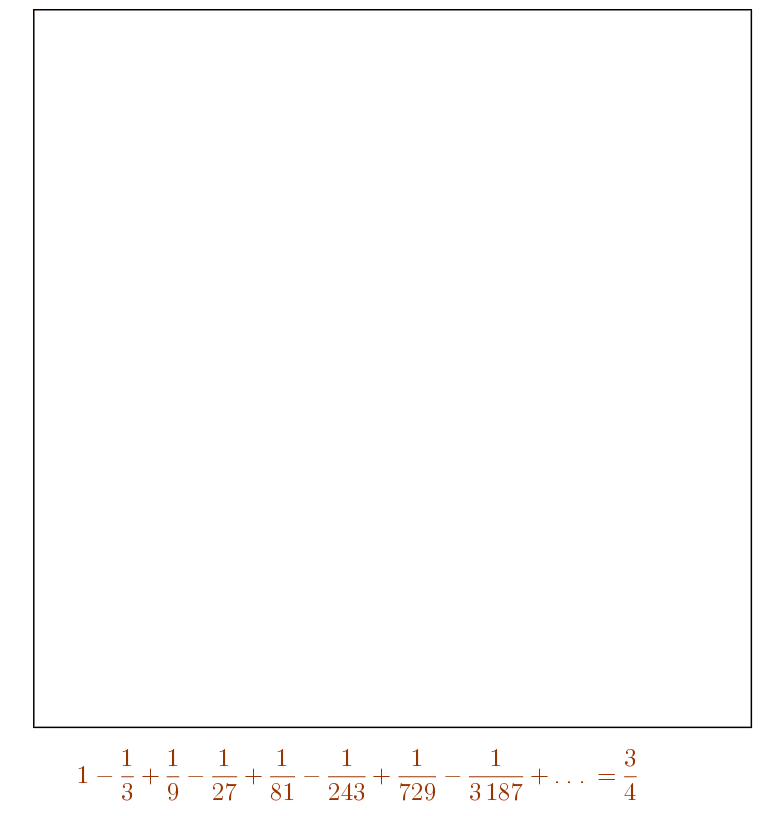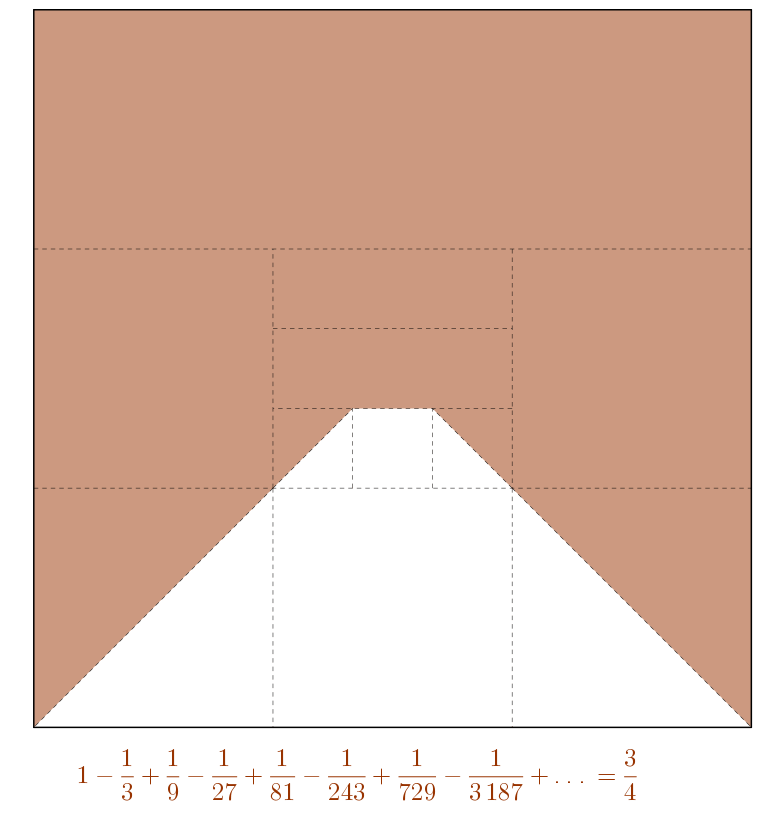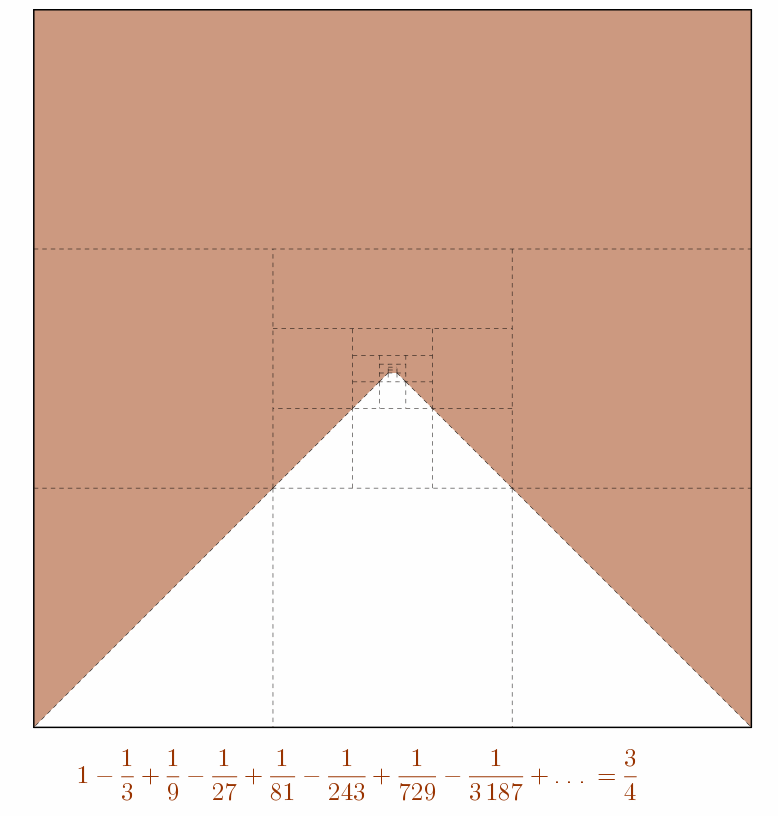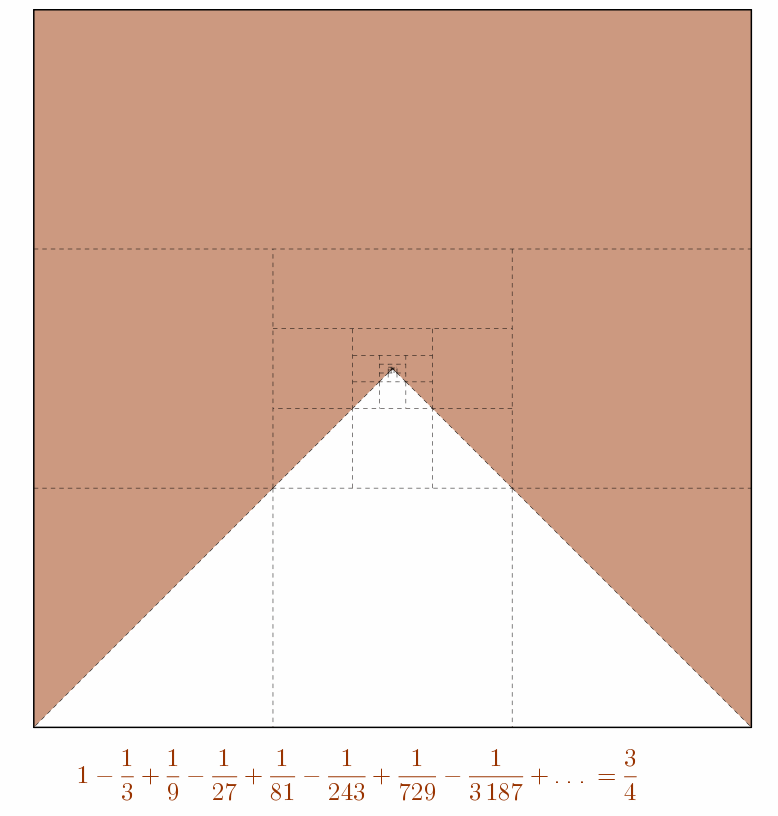
Références :
Nelsen, Roger B., Proof Without Words, MAA Press (1993)
Nelsen, Roger B., Proofs Without Words II: More Exercises in Visual Thinking, MAA Press (2000)
Nelsen, Roger B., Proofs Without Words III: Further Exercises in Visual Thinking, MAA Press (2015)