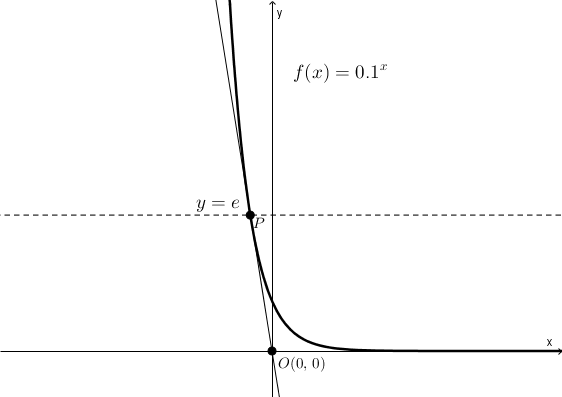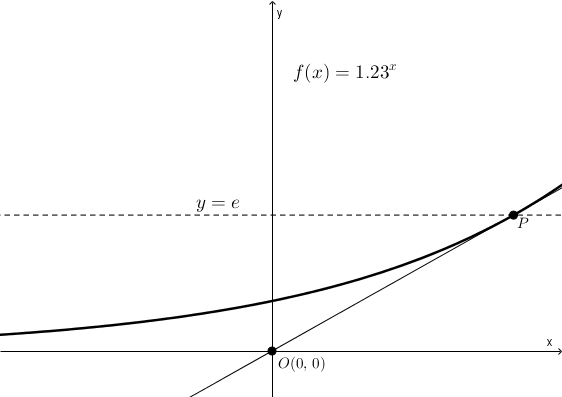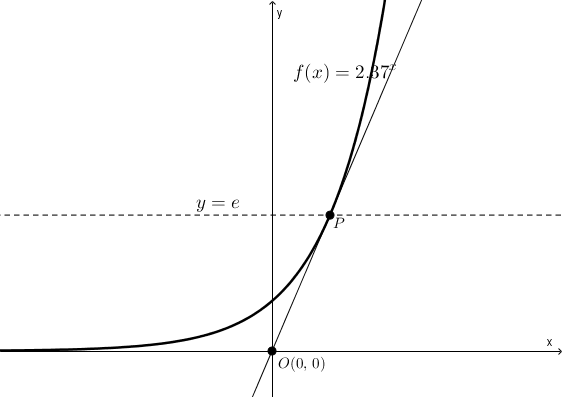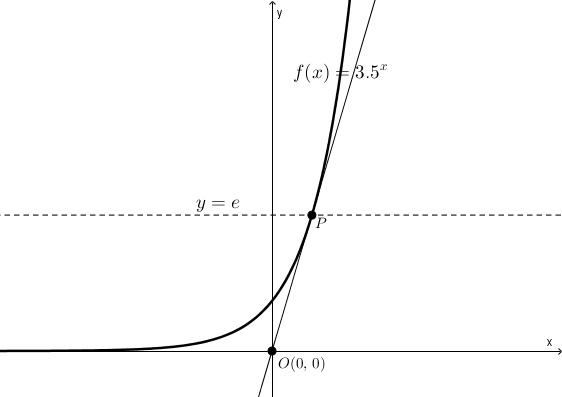
On considère une fonction exponentielle d’équation \[f(x) = c^{x}\]et on s’intéresse à la tangente à cette fonction passant par l’origine du plan cartésien. Supposons que le point de tangence soit\[P\left(x_{0},\, f(x_{0})\right)\]
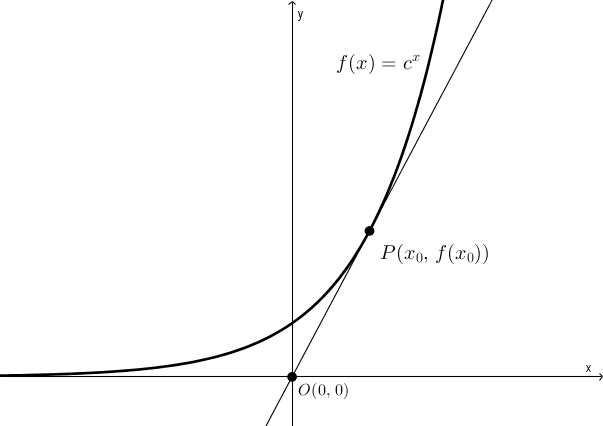
Certainement, la pente de la tangente sera donnée d’une part par\[\frac{f(x_{0})-0}{x_{0}-0} = \frac{f(x_{0})}{x_{0}}\]et d’autre part par (c’est la valeur de la dérivée en \(x_{0}\)) \[f'(x_{0})\]On trouve, en égalant les deux expressions de la pente,\[\frac{f(x_{0})}{x_{0}} = f'(x_{0})\]et puisque \[f'(x) = \ln(c) \cdot c^{x}\]on obtient \[\frac{c^{x_{0}}}{x_{0}} = \ln(c)\cdot c^{x_{0}}\]On trouve comme solution\begin{align*}\frac{1}{x_{0}} &= \ln(c)\cdot 1 \\ \\ x_{0} &=\frac{1}{\ln(c)}\end{align*}À l’aide d’un changement de base, on réécrit \begin{align*}x_{0} &= \frac{1}{\ln(c)} \\ \\ &= \frac{1}{\frac{\log_{c}(c)}{\log_{c}(e)}} \\ \\ &=\frac{1}{\frac{1}{\log_{c}(e)}} \\ \\ &=\log_{c}(e)\end{align*}C’est l’abscisse du point de tangence. L’ordonnée est \begin{align*}f(x_{0}) &= f\left(\log_{c}(e)\right) \\ \\ &= c^{\log_{c}(e)} \\ \\ &= e\end{align*}Il est tout à fait remarquable (et apparemment peu connu) que la valeur de l’ordonnée, \(e\), le nombre d’Euler, ne dépend pas du choix de la base de l’exponentielle. Les coordonnées de \(P\) sont toujours \[P\left(\log_{c}(e),\, e\right)\]qu’importe la valeur choisie pour \(c\).
Référence : Branko Ćurgus (2006), The College Mathematics Journal Vol 37, pp. 344-354
Bonjour, l’argumentation de la premiere expression donnant la pente de la tangente n’est pas claire. Je pense qu’au lieu de parler de fonction lineaire (alors qu’on parle de droite) il faut considerer la pente de la droite (son coefficient directeur) ( qui dans ce cas passe par l’origine) , lequel peut etre caslculé comme vous l’avez fait. Ceci d’une part, d’autre part,qui nous dit qu’il existe une telle tangente?( une demonstration est necessaire)
Merci pour l’idée.
Bonjour Wafi,
j’ai noté les commentaires et j’ai essayé d’être plus clair (je ne parle plus de fonction linéaire et j’ai mis le calcul des accroissements des abscisses et ordonnées pour être plus transparent).
Pour la démonstration, une fonction exponentielle f(x) = c^x est dérivable et la tangente au point P(x0, y0) passe par l’origine seulement si
f'(x0) = f(x0)/x0. Dans notre cas, je crois qu’il suffit de choisir correctement x0 comme 1/ln(c) et le reste devrait suivre.
Pour un traitement plus approfondi sur des familles larges de fonctions possédant cette propriété, je vous renvoie à
Dietel & Gordon, Off on a Tangent. The College Mathematics Journal, Vol.34 2003