Quel est le rapport de la hauteur et du rayon du plus grand cône circulaire droit si l’aire latérale est donnée ? [1] Le volume du cône est \[V = \frac{\pi \cdot r^{2} \cdot h}{3}\]où \(r\) est le rayon de la base et \(h\) est la hauteur du cône. On se rappelle que le cône est une surface développable : on obtient un secteur de disque.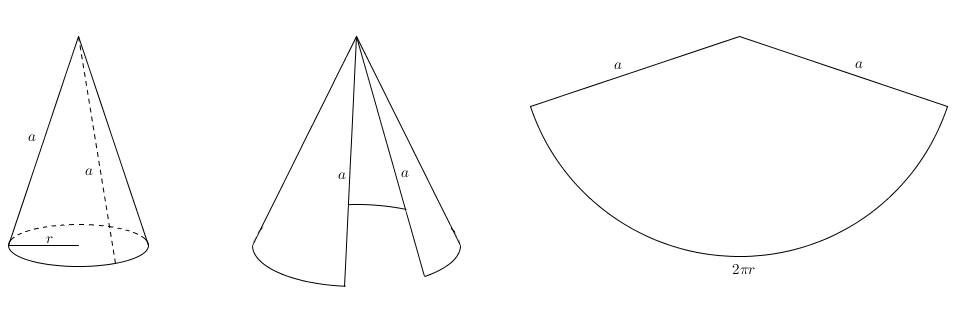
Tel que vu ici, l’aire du secteur, c’est-à-dire l’aire latérale du cône, est \[L = a\cdot \pi \cdot r\]Enfin, comme la hauteur, le rayon de la base et l’apothème du cône forment un triangle rectangle, on peut poser, avec Pythagore \[r^{2} + h^{2} = a^{2}\]Cela nous donne une expression pour \(h^{2}\), \[h^{2} = a^{2}-r^{2}\]En utilisant la formule de l’aire latérale, on a aussi \begin{align*}L&=a \cdot \pi \cdot r \\ \\ \frac{L}{\pi \cdot r} &=a\end{align*}En remplaçant on obtient \begin{align*}h^2 &= a^2 – \ r^2 \\ \\ &=\left(\frac{L}{\pi \cdot r}\right)^{2}-\, r^{2} \\ \\ &=\frac{L^2}{\pi^{2}\cdot r^{2}} -r^{2}\end{align*}ce qui fait finalement \[h = \sqrt{\frac{L^2}{\pi^{2}\cdot r^{2}}-r^{2}}\]Cette expression pour la hauteur nous permettra d’exprimer le volume avec seule \(r\) comme variable. \begin{align*}V &= \frac{\pi \cdot r^{2}\cdot h}{3} \\ \\ &= \frac{\pi }{3} \cdot r^{2}\cdot \sqrt{\frac{L^2}{\pi^{2}\cdot r^{2}}-r^{2}} \\ \\ &=\frac{\pi}{3} \cdot \sqrt{r^{4}\cdot \left(\frac{L^2}{\pi^{2}\cdot r^{2}}-r^{2}\right)} \\ \\ &=\frac{\pi}{3} \cdot \sqrt{\frac{L^{2}\cdot r^{2}}{\pi^{2}}-r^{6}}\end{align*} Ce n’est pas joli, mais on fera avec !
La dérivée du volume par rapport au rayon est [2] \[\frac{\mathrm{d}V}{\mathrm{d}r} = \frac{\pi}{3}\cdot \frac{1}{2\sqrt{\frac{L^2\cdot r^2}{\pi^2}-r^6}} \cdot \left(\frac{2\cdot L^2\cdot r}{\pi^2}-6r^5\right)\]ou, de manière équivalente, \[\frac{\mathrm{d}V}{\mathrm{d}r} = \frac{\pi}{3}\cdot \frac{1}{2\sqrt{\frac{L^2 r^2}{\pi^2}-r^6}} \cdot \left(\frac{2 L^2 r-6\pi^2 r^5}{\pi^2}\right)\] ou encore, \[\frac{\mathrm{d}V}{\mathrm{d}r} = \frac{L^2 r-3\pi^2 r^5}{3\pi\sqrt{\frac{L^2 r^2}{\pi^2}-r^6}}\]On peut poser \(\frac{\mathrm{d}V}{\mathrm{d}r} = 0\) et résoudre. \[\frac{L^2 r-3\pi^2 r^5}{3\pi\sqrt{\frac{L^2 r^2}{\pi^2}-r^6}} = 0\]En considérant le numérateur, \[L^2r-3\pi^2r^5 = 0\]on peut factoriser \[r\left(L^{2}-3\pi^2r^4\right) = 0\]afin d’obtenir soit \(r = 0\), soit \(L^2-3\pi^2 r^4 = 0\). Dans le deuxième cas, on obtient \begin{align*}L^2 &= 3\pi^2 r^4 \\ \\ \frac{L^2}{3\pi^2} &= r^4 \\ \\ \frac{L}{\sqrt{3}\pi} &= r^{2}\\ \\ \sqrt{\frac{L}{\sqrt{3}\pi}} &= r\end{align*} On a donc une expression pour le rayon en fonction de l’aire latérale. On peut retrouver la valeur de \(h\) en remplaçant dans \[h = \sqrt{\frac{L^2}{\pi^{2} r^{2}}-r^{2}}\]Ce n’est toujours pas joli, mais quelques étapes algébriques nous permettent d’obtenir \begin{align*} h&=\sqrt{\frac{L^2}{\pi^{2} \frac{L}{\sqrt{3}\pi}}-\frac{L}{\sqrt{3}\pi}}\\ \\ &= \sqrt{\frac{\sqrt{3}L}{\pi} – \frac{L}{\sqrt{3}\pi}} \\ \\ &= \sqrt{\frac{3L}{\sqrt{3}\pi} – \frac{L}{\sqrt{3}\pi}} \\ \\ &=\sqrt{\frac{2L}{\sqrt{3}\pi}}\end{align*}
Enfin, il est possible de calculer le rapport optimal : \begin{align*}\frac{h}{r}&=\frac{\sqrt{\frac{2L}{\sqrt{3}\pi}}}{\sqrt{\frac{L}{\sqrt{3}\pi}}}\\ \\&=\frac{\sqrt{2}\cdot \sqrt{\frac{L}{\sqrt{3}\pi}}}{\sqrt{\frac{L}{\sqrt{3}\pi}}}\\ \\ &=\sqrt{2}\end{align*}
Le rapport entre la hauteur du cône et le rayon est \(\sqrt{2}\) [3]. On peut aussi calculer le volume maximal (exprimé avec \(L\)). \begin{align*}V&=\frac{\pi}{3} \cdot r^2 \cdot h \\ \\ &=\frac{\pi}{3}\cdot \frac{L}{\sqrt{3}\pi}\cdot \sqrt{\frac{2L}{\sqrt{3}\pi}} \\ \\ &= \sqrt{\frac{\pi^2}{9}} \cdot \sqrt{\frac{L^2}{3\pi^2}} \cdot \sqrt{\frac{2L}{\sqrt{3}\pi}} \\ \\ &=\sqrt{\frac{2L^3}{27\sqrt{3}\pi}}\end{align*}
En prime, on reprend \[r^2 + h^2 = a^2\]et on remplace,\[r^2 + \left(\sqrt{2}r\right)^2 = a^2\]ce qui fait\[r^2 + 2r^2 = a^2\]et donc\[3r^2 = a^2\]dont on tire\[\sqrt{3}r = a\]En reprenant le secteur circulaire, avec, ici, le cercle complet de rayon \(a\), on a \[\frac{\theta}{360^{\circ}} = \frac{2\cdot \pi \cdot r}{2\cdot \pi \cdot a}\]puisque l’angle au centre est proportionnel à la longueur de l’arc intercepté.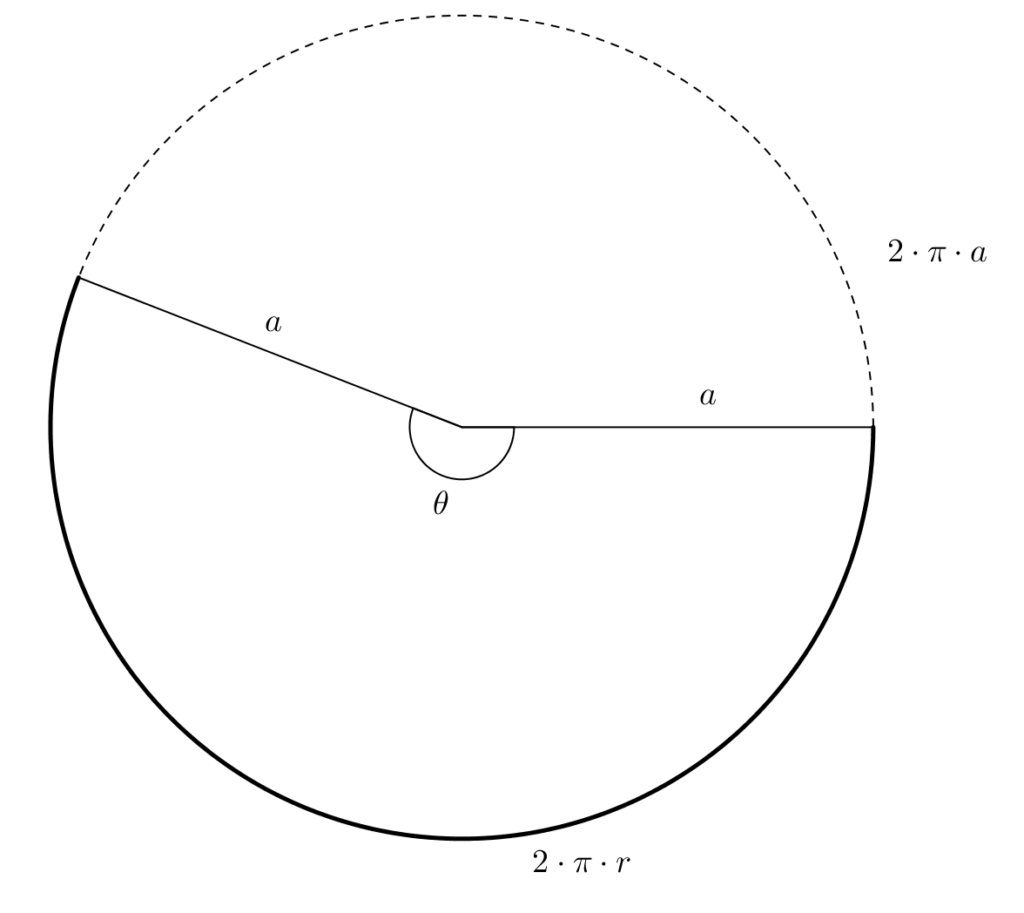
En remplaçant, \[\frac{\theta}{360^{\circ}} = \frac{2\cdot \pi \cdot r}{2\cdot \pi \cdot \sqrt{3}r}\]puis en simplifiant et multipliant, on obtient \[\theta \ =\ 360^{\circ} \cdot \frac{1}{\sqrt{3}}\ \approx\ 207,846^{\circ}\]Ainsi, pour construire un cône de volume maximal avec une aire latérale donnée, on devrait déterminer dans le grand disque un angle au centre d’environ 208°. Bien que les équations données précédemment décrivent précisément le cône, en particulier la hauteur et le rayon, à partir de l’aire latérale \(L\), comment ferait-on pour construire ledit cône étant donné \(L\) ? On se rappelle que l’aire du secteur est proportionnel à l’angle au centre [4], \[\frac{L}{\pi \cdot a^2}=\frac{1}{\sqrt{3}}\]On trouve donc \begin{align*}\frac{\sqrt{3}L}{\pi} &= a^2 \\ \\ \sqrt{\frac{\sqrt{3}L}{\pi}} &= a\end{align*}À titre d’exemple, on construit un cône dont l’aire latérale est égale à 355 cm2. On trace un cercle de rayon \[a = \sqrt{\frac{\sqrt{3}\cdot 355}{\pi}} \approx 14\]en cm. On mesure ensuite un angle au centre d’environ 208° et on découpe !
[1] Je ne me rappelle plus des détails, mais il y a une bonne dizaine d’années, j’avais lu, dans le magazine Tangente, dans un dossier sur l’empirisme, que les Amérindiens construisaient des tipis de manière optimale ou presque ; tout comme d’autres peuples ailleurs dans le monde accomplissaient aussi d’autres activités de manière optimale (je crois que l’exemple des Romains était de tuer un homme d’un coup de couteau au cœur, joie!). L’aire latérale, dans le cas du tipi, étant faite de peaux, on comprend la nécessité de maximiser le volume. L’article relatait que ces habiletés étaient le fruit d’une “analyse” empirique à très long terme, des savoirs qui se passaient de génération en génération. Comme on dit, c’est en forgeant qu’on devient forgeron ! Ceci étant dit, je ne crois pas que le tipi de l’image du début du billet, tirée de Wikipedia, respecte les conclusions de ce billet !
[2] La dérivée de \(f(x) = \sqrt{g(x)}\) est \(f'(x) = \frac{1}{2\sqrt{x}}\cdot g'(x)\).
[3] Un problème semblable fréquemment rencontré est celui-ci : on doit déterminer le rapport entre le rayon et la hauteur du cône de plus grand volume construit à partir d’un disque de rayon \(a\) (tel que résolu ici, par exemple : https://youtu.be/dNSk4coSpUc). De manière équivalente, c’est le volume maximal d’un cône d’apothème donnée. Le rapport dans cet autre problème est aussi \(\sqrt{2}\), mais c’est la valeur du rapport inverse, c’est-à-dire \(\frac{r}{h}\) au lieu de \(\frac{h}{r}\). De mémoire, on doit découper dans le disque un secteur circulaire dont l’angle au centre est environ 294°. Une recherche de « maximiser le volume d’un cône » sur Internet, en français ou en anglais, nous amène vers la résolution de ce problème (dans lequel \(a\) est donné) ou celui du cône de volume maximal inscrit dans une sphère. J’ai trouvé bien peu de ressources sur le cône de volume maximal avec une aire latérale donnée, d’où ce billet !
[4] On aurait pu aussi réutiliser \(r^2 + h^2 = a^2\). On obtient \begin{align*}\frac{L}{\sqrt{3}\pi} + \frac{2L}{\sqrt{3}\pi} &= a^2 \\ \\ \frac{3L}{\sqrt{3}\pi} &= a^2 \\ \\ \frac{\sqrt{3}L}{\pi} &= a\end{align*}